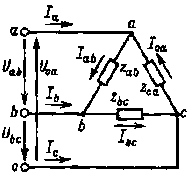

Как видно из схемы рис. 3.12, каждая фаза приемника при соединении треугольником подключена к двум линейным проводам. Поэтому независимо от значения и характера сопротивлений приемника каждое фазное напряжение равно соответствующему линейному напряжению:
U ф = U л. (3.16)
Если не учитывать сопротивлений проводов сети, то напряжения приемника следует считать равными линейным напряжениям источника.
На основании схемы рис. 3.12 и выражения (3.16) можно сделать вывод о том, что соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника или однофазные приемники рассчитаны на напряжение, равное номинальному линейному напряжению сети.
Фазные токи Iab, Ibc и Iса в общем случае не равны линейным токам Ia, Ib и Ic. Применяя первый закон Кирхгофа к узловым точкам а, b и с, можно получить следующие соотношения между линейными и фазными точками:
I a = I ab - I ca, I b = I bc - I ab, I c = I ca - I bc. (3.17)
Используя указанные соотношения и имея векторы фазных токов, нетрудно построить векторы линейных токов.
Симметричная нагрузка. В отношении любой фазы справедливы все формулы, полученные ранее для однофазных цепей, например
(3.18)
| } |

Очевидно, при симметричной нагрузке
Iab = Ibc = Ica = Iф;
φab = φbc = φca = φф;
Pab = Pbc = Pca = Pф;
Qab = Qbc = Qca = Qф;
Sab = Sbc = Sca = Sф.
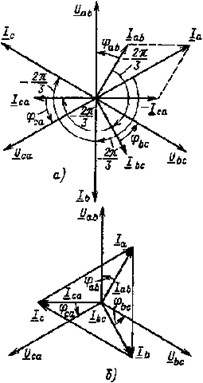
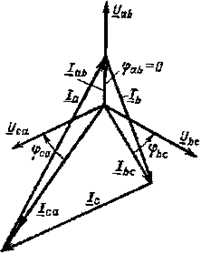
Векторная диаграмма фазных (линейных) напряжений, а также фазных токов при симметричной активно-индуктивной нагрузке приведена на рис. 3.13, а. Там же в соответствии с выражениями (3.17) построены векторы линейных токов. Следует обратить внимание на то, что при изображении векторных диаграмм в случае соединения треугольником вектор линейного напряжения Uab принято направлять вертикально вверх.
Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке существуют симметричные системы фазных и линейных токов.
Векторы линейных токов чаще изображают соединяющими векторы соответствующих фазных токов, как показано на рис. 3.13, б. На основании векторной диаграммы рис. 3.13, б
Ia = 2 Iab sin 60° = √3 Iab,
Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно написать, что при симметричной нагрузке вообще
Ia =√3 I ф. (3.19)
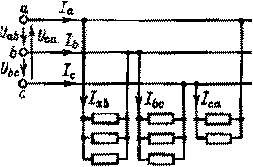

Несимметричная нагрузка. Как и при соединении звездой, в случае соединения треугольником однофазные приемники делят на три примерно равные в отношении мощности группы. Каждая группа подключается к двум проводам, между которыми имеется напряжение, отличающееся по фазе от двух других напряжений сети (рис. 3.14). В пределах каждой группы приемники соединяются параллельно.
После замены приемников каждой фазы одним приемником с эквивалентным сопротивлением и соответствующего их расположения получим схему, приведенную на рис. 3.12.
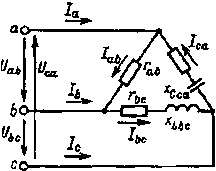
Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также фазные мощности можно определить по формулам (3.18). При несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными. Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bс — активно-индуктивная, а в фазе са — активно-емкостная (рис. 3.15), приведена на рис. 3.16. Построение векторов линейных токов произведено в соответствии с выражениями (3.17).

Для определения мощностей всех фаз следует пользоваться формулами:
P = Pab + Pbc + Pca, Q = Qab + Qbc + Qca, (3.20)

Формулы (3.13) и (3.14), полученные ранее для симметричной нагрузки, не пригодны для определения мощностей при несимметричной нагрузке.
Если кроме фазных токов требуется определить линейные токи, задачу следует решать в комплексной форме. Для этой же цели можно воспользоваться векторной диаграммой.
При решении задачи в комплексной форме необходимо прежде всего выразить в комплексной форме фазные напряжения, а также полные сопротивления фаз. Когда это сделано, нетрудно по закону Ома определить фазные токи. Например, комплексное выражение тока Iab будет
I ab = U ab /Z ab. (3.21)
Линейные токи определяются через фазные с помощью выражений (3.17).
Комплексным методом можно воспользоваться и для определения фазных мощностей. Так, мощности фазы аb будут равны
S ab = U ab I *ab = Re S ab, (3.22)
Qab = Im S ab; S ab = √ P 2 ab + Q 2 ab.
Рассмотрим, как будут изменяться значения различных величин в электрической цепи рис. 3.15 при изменении сопротивления приемников. Например, если при xCca /rca = const увеличить вдвое сопротивление zca, то ток Ica уменьшится, а угол φ ca не изменится (см. рис. 3.16). Очевидно, при этом уменьшатся и токи Iа, Ic, а также мощности Рса, Qса, Sса. Токи Iаb, Ibc, Ib, углы φ ab, φ bc, а также мощности Рab, Qab, Sab, Рbc, Qbc, Sbc останутся постоянными. При отключения фазы са сопротивление
zca = ∞, Iса = 0, токи Iаb, Ibc, Ib, а также углы φ ab, φ bc не изменятся, а токи Iа и Ic уменьшатся I a = I ab, I c = - I bc.
23. Мощности в трехфазных цепях и способы их измерения.
Активная и реактивная мощности трехфазной цепи, как для любой сложной цепи, равны суммам соответствующих мощностей отдельных фаз:
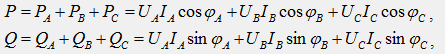
где IA, UA, IB, UB, IC, UC – фазные значения токов и напряжений.
В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи может быть получена путем умножения фазных мощностей на число фаз:
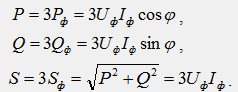
В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения Uф/Uл/√3, Iф=Iл, тогда получим:
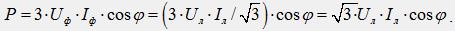
Для схемы треугольника верны соотношения: Uф=Uл; Iф=Iл / √3, тогда получим:
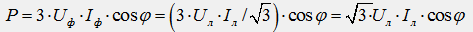
Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи формулы для мощностей имеют одинаковый вид:
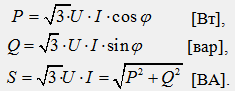
В приведенных формулах для мощностей трехфазной цепи подразумеваются линейные значения величин U и I, но индексы при их обозначениях не ставятся.
Активная мощность в электрической цепи измеряется прибором, называемым ваттметром, показания которого определяется по формуле:
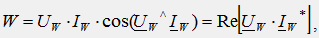
где Uw, Iw - векторы напряжения и тока, подведенные к обмоткам прибора.
Для измерения активной мощности всей трехфазной цепи в зависимости от схемы соединения фаз нагрузки и ее характера применяются различные схемы включения измерительных приборов.
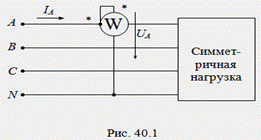
Для измерения активной мощности симметричной трехфазной цепи применяется схема с одним ваттметром, который включается в одну из фаз и измеряет активную мощность только этой фазы (рис. 40.1). Активная мощность всей цепи получается путем умножения показания ваттметра на число фаз: P=3W=3UфIфcos(φ). Схема с одним ваттметром может быть использована только для ориентированной оценки мощности и неприменима для точных и коммерческих измерений.
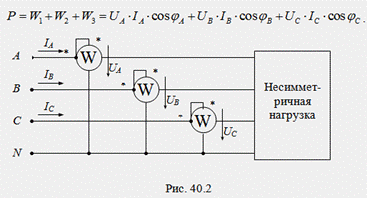
Для измерения активной мощности в четырехпроводных трехфазных цепях (при наличии нулевого провода) применяется схема с тремя приборами (рис. 40.2), в которой производится измерение активной мощности каждой фазы в отдельности, а мощность всей цепи определяется как сумма показаний трех ваттметров:
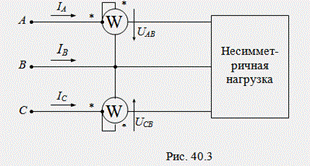
Для измерения активной мощности в трехпроводных трехфазных цепях (при отсутствии нулевого провода) применяется схема с двумя приборами (рис. 40.3).
При отсутствии нулевого провода линейные (фазные) ток связаны между собой уравнением 1-го закона Кирхгофа: IA+IB+IC=0. Сумма показаний двух ваттметров равна:
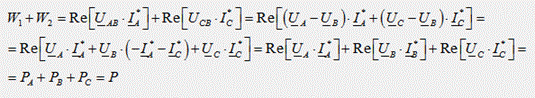
Таким образом, сумма показаний двух ваттметров равна активной трехфазной мощности, при этом показание каждого прибора в отдельности зависит не только величины нагрузки, но и от ее характера.
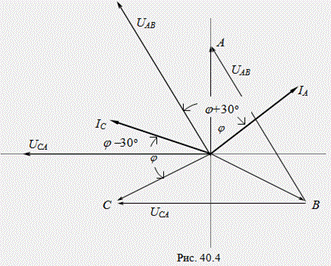
На рис. 40.4 показана векторная диаграмма токов и напряжений для симметричной нагрузки. Из диаграммы следует, что показания отдельных ваттметров могут быть определены по формулам:
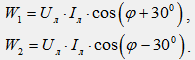
Анализ полученных выражений позволяет сделать следующие выводы. При активной нагрузке (φ = 0), показания ваттметров равны (W1 = W2).
При активно-индуктивной нагрузке(0 ≤ φ ≤ 90°) показание первого ваттметра меньше, чем второго (W1 < W2), а при φ>60° показание первого ваттметра становится отрицательным (W1<0).
При активно-емкостной нагрузке(0 ≥ φ≥ -90°) показание второго ваттметра меньше, чем первого (W1 больше W2), а при φ(меньше)-60 ° показание второго ваттметра становится отрицательным.
| 24) Магнитное поле и его характеристики. Магнитная цепь электромагнитного реле. | ||
 Рисунок 4. Забегая вперёд, скажу, что таков вид магнитных силовых линий, возникающих вокруг проводника с током. Рисунок 4. Забегая вперёд, скажу, что таков вид магнитных силовых линий, возникающих вокруг проводника с током. | Согласно теории близкодействия ток в одном из проводников не может непосредственно действовать на ток в другом проводнике. Подобно тому как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле,в пространстве, окружающем токи, возникает поле, называемое магнитным. Электрический ток в одном из проводников создаёт вокруг себя магнитное поле, которое действует на ток в другом проводнике. А поле, созданное электрическим током второго проводника, действует на первый. МАГНИТНОЕ ПОЛЕ представляет собой особую форму материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами. | |
Основные свойства магнитного поля:
1. Магнитное поле порождается электрическим током (= движущимися зарядами).
2. Магнитное поле обнаруживается по действию на электрический ток (= движущиеся заряды).
3. Подобно электрическому полю, магнитное поле существует реально независимо от нас, от наших знаний о нём. Экспериментальным доказательством реальности магнитного поля, как и реальности электрического поля, является факт существования электромагнитных волн (то есть посылка и приём радио- и телевизионных сигналов).
Реле? (фр. relais) — электромеханическое устройство (выключатель), предназначенное для коммутации электрических цепей при заданных изменениях электрических или неэлектрических входных величин. Различают электромагнитные, пневматические и температурные реле.
Существует класс электронных полупроводниковых приборов именуемых оптореле (твердотельное реле)
В электронной схемотехнике иногда электронные блоки с функцией переключения цепи по изменению какого-либо физического параметра также называют реле. Например, фотореле, реле контроля фаз или реле-прерыватель указателей поворота автомобиля.
Электромагнитное реле представляет собой прибор, в котором при достижении определенного значения входной величины выходная величина изменяется скачком и предназначено для применения в цепях управления, сигнализации.
Существует много разновидностей реле как по принципу действия, так и по назначению. Бывают реле механические, гидравлические, пневматические, тепловые, акустические, оптические, электрические и др.
По назначению они подразделяются на реле автоматики, реле защиты, исполнительные реле, реле промежуточные, реле связи.
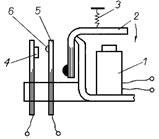
Устройство. Рассмотрим в качестве примера электромагнитное реле с поворотным якорем (рис. 1). В этом реле различают две части: воспринимающую электрический сигнал и исполнительную.
• Воспринимающая часть состоит из электромагнита 1, представляющего собой катушку, надетую на стальной сердечник, якоря 2 и пружины 3.
• Исполнительная часть состоит из неподвижных контактов 4, подвижной контактной пластины 5, посредством которой воспринимающая часть реле воздействует на исполнительную, и контактов 6.
Следует обратить внимание на то, что воспринимающая и исполнительная части реле не имеют между собой электрической связи и включаются в разные электрические цепи.
Реле приводится в действие слабым (малоточным) сигналом, и само может приводить в действие более мощную исполнительную аппаратуру (контактор, масляный выключатель, пускатель и т. д.).
Принцип действия. Когда ток в катушке электромагнита отсутствует, якорь под действием пружины удерживается в верхнем положении, при этом контакты реле разорваны.
При появлении тока в катушке электромагнита якорь притягивается к сердечнику и подвижный контакт замыкается с неподвижным. Происходит замыкание исполнительной цепи, т. е. включение того или иного подсоединенного исполнительного устройства.
В зависимости от исполнения реле комплектуются розетками под пайку, под DIN-рейку или розетками под винт.
 2015-05-13
2015-05-13 30016
30016
