I. Обыкновенные дифференциальные уравнения (ДУ) I-го порядка.
1.1. Задачи, приводящие к дифференциальным уравнениям. Определения.
Литература:  , гл. XIII, §1-2, упр. 1,2,4.
, гл. XIII, §1-2, упр. 1,2,4.
1.2. Уравнения с разделяющимися переменными.
Литература:  , гл. XIII, §4, упр. 9, 20-26, 35-37.
, гл. XIII, §4, упр. 9, 20-26, 35-37.
1.3. Однородные ДУ 1-го порядка и приводящиеся к ним.
Литература:  , гл. XIII, §5, упр. 40-47, 55, 56, §6, упр. 48-50.
, гл. XIII, §5, упр. 40-47, 55, 56, §6, упр. 48-50.
1.4. Линейные ДУ 1-го порядка и уравнение Бернулли.
Литература:  , гл. XIII, §7, упр. 58-63, §8, упр. 66-69.
, гл. XIII, §7, упр. 58-63, §8, упр. 66-69.
1.5. Уравнения в полных дифференциалах.
Литература:  , гл. XIII, §9, 10, упр. 72-76, 80.
, гл. XIII, §9, 10, упр. 72-76, 80.
1.6. Огибающая семейства кривых. Особые решения ДУ 1-го порядка.
Литература:  , гл. XIII, §11, 12.
, гл. XIII, §11, 12.
Вопросы для самопроверки.
- Дайте определения:
а) дифференциального уравнения 1-го порядка;
б) общего решения ДУ 1-го порядка;
в) общего интеграла ДУ 1-го порядка;
г) частного решения (интеграла) ДУ 1-го порядка. - Сформулируйте задачу Коши для ДУ 1-го порядка и укажите ее геометрический смысл.
- Дайте определения:
а) интегральной кривой ДУ 1-го порядка;
б) семейства интегральных кривых ДУ, дайте геометрическое толкование ДУ 1-го порядка. - Сформулируйте теорему о существовании и единственности решения ДУ 1-го порядка. Что называется особым решением ДУ 1-го порядка?
- Дайте определения ДУ:
а) с разделенными переменными;
б) с разделяющимися переменными.
Изложите метод нахождения общего решения ДУ с разделяющимися переменными. Найдите общее решение уравнения:
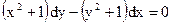 .
. - Дайте определение однородного ДУ 1-го порядка. С помощью какой замены переменной однородное ДУ приводится к уравнению с разделяющимися переменными? Являются ли однородными уравнения:
а)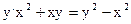 ; б)
; б) 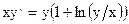 ?
?
С помощью какой подстановки уравнение вида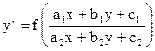 при
при 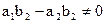 приводится к однородному?
приводится к однородному? - Дайте определение линейного ДУ 1-го порядка: а) однородного; б) неоднородного. Изложите: а) метод Бернулли решения ЛНДУ 1-го порядка; б) метод вариации произвольной постоянной (метод Лагранжа). Является ли уравнение
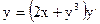 линейным относительно функции
линейным относительно функции 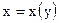 ?
? - Дайте определение уравнения Бернулли. Покажите, что с помощью подстановки
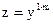 (где z – новая функция) уравнение Бернулли преобразуется к линейному. Какие методы решения уравнения Бернулли вы знаете?
(где z – новая функция) уравнение Бернулли преобразуется к линейному. Какие методы решения уравнения Бернулли вы знаете?
II. Дифференциальные уравнения высших порядков.
2.1. Общие понятия.
Литература:  , гл. XIII, §16, упр. 117.
, гл. XIII, §16, упр. 117.
2.2. Уравнения, допускающие понижение порядка.
Литература:  , гл. XIII, §17, упр. 118, 119, §18, упр. 120-124.
, гл. XIII, §17, упр. 118, 119, §18, упр. 120-124.
2.3. Линейные ДУ 2-го порядка.
Литература:  , гл. XIII, §20,21, упр. 129-132, 140-146, §23-25, упр. 149-158, 164-167.
, гл. XIII, §20,21, упр. 129-132, 140-146, §23-25, упр. 149-158, 164-167.
Вопросы для самопроверки.
- Дайте определения: а) ДУ 2-го порядка; б) его общего и частного решений. Сформулируйте задачу Коши для ДУ 2-го порядка, укажите его геометрический смысл.
- Изложите методы решений ДУ вида:
а)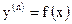 б)
б) 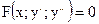 в)
в) 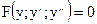
- Дайте определение: а) линейного ДУ n-го порядка (однородного и неоднородного (ЛОДУ и ЛНДУ)); б) линейно зависимых и линейно независимых функций; в) определителя Вронского; г) фундаментальной системы решений.
Сформулируйте условия линейной независимости решений ЛОДУ. Исследуйте на линейную независимость следующие системы функций: 1) х; lnx; 2)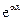 ;
; 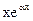 ; 3) х; х2.
; 3) х; х2.
Сформулируйте необходимое условие линейной зависимости системы функций. - Сформулируйте терему о структуре общего решения: а) ЛОДУ; б) ЛНДУ.
Докажите, что сумма частных решений уравнений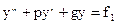 и
и 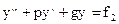 является решением уравнения
является решением уравнения 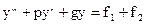 .
. - Изложите метод Лагранжа вариации произвольных постоянных.
- Выведите формулу для общего решения линейного однородного ДУ 2 порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения.
- Изложите правило нахождения частного решения линейного ДУ 2 порядка с постоянными коэффициентами и правой частью вида: а)
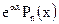 , где
, где 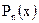 - многочлен степени
- многочлен степени 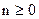 ; б)
; б) 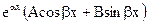 .
.
 2015-05-13
2015-05-13 656
656






