Дискриминантный анализ

Дискриминантный анализ относится к группе методов анализа зависимости и внешний вид получаемой дискриминантной функции не отличается от уравнения регрессии: D = b₀ + b₁x₁+ b₂x₂ +..+ b_kx_k. В качестве зависимой переменной выступает номинальная переменная, идентифицирующая принадлежность объектов к одной из нескольких групп. Независимые переменные (x₁, x₂.. x_k) количественные и качественные.

Основной задачей дискриминантного анализа является исследование групповых различий - различие (дискриминация) объектов по определенным признакам. Дискриминантный анализ позволяет выяснить, действительно ли группы различаются между собой, и если да, то каким образом (какие переменные вносят наибольший вклад в имеющиеся различия).

При сравнении двух групп (бинарная зависимая переменная) формируется одна дискриминантная функция. Если данный метод применяется к анализу трех или более групп (множественный дискриминантный анализ), то могут формироваться несколько дискриминантных функций.

Важной проблемой дискриминантного анализа является определение дискриминантных переменных (переменных, входящих в дискриминантную функцию). Возможны два подхода. Первый предполагает одновременное введение всех переменных, в этом случае учитывается каждая независимая переменная, при этом ее дискриминирующая сила не принимается во внимание. Альтернативой является пошаговый (stepwise) дискриминантный анализ, при котором переменные вводятся последовательно, исходя из их способности различить (дискриминировать) группы. При пошаговом анализе «с включением» на каждом шаге просматриваются все переменные, и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная должна быть включена в модель на данном шаге, и происходит переход к следующему шагу.

При пошаговом анализе «с исключением» движутся в обратном направлении, в этом случае все переменные сначала будут включены в модель, а затем на каждом шаге будут устраняться переменные, вносящие малый вклад в различение. Тогда в качестве результатауспешного анализа можно сохранить только «важные» переменные в модели, т.е. те переменные, чей вклад в дискриминацию больше остальных. Пошаговый дискриминантный анализ основан на использовании уровня значимости F-статистики.

Проверка качества дискриминации (различия) основана на сравнении средних дискриминантной функции для исследуемых групп. Эти средние играют настолько важную роль в дискриминантном анализе, что получили свое название – центроиды (centroids). Центроидов столько, сколько групп, т.е. один центроид для каждой группы. Кроме этого, значения дискриминантной функции также имеют свое название – дискриминантные показатели (discriminant scores).

Кроме предположения о мультиколлинеарности для корректного применения дискриминантного анализа также должны выполняться предпосылки нормальности распределения независимых переменных и однородности дисперсий/ковариаций (проверяется с помощью М-статистики Бокса (Box’s M)).

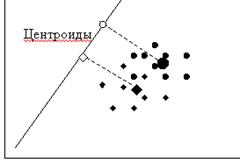
Рисунок 2.1 – Классификация дискриминантной функцией

Для нового объекта находится его проекция на дискриминантную ось (т.е. значение дискриминантной функции – дискриминантный показатель) и определяется, к какому из центроидов (для первой или второй группы) он более близко расположен. Соответственно, он будет отнесен к этой группе. Степень «близости» может определяться с помощью пороговых значений (если размеры групп равны, то пороговое значение – среднее арифметическое двух центроидов, если же группы не равны, то вычисляется средневзвешенная).

Задачу построения оптимальной процедуры классификации многомерных наблюдений можно сформулировать следующим образом. Заданы p - мерные наблюдения 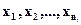представляющие собой выборку из генеральной совокупности, описываемой так называемой смесью из m классов с плотностью вероятности

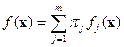(2.1)

где 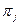- априорная вероятность появления в этой выборке элемента из класса 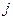с плотностью 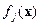. Другими словами, 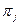- удельный вес элементов 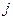-го класса в общей генеральной совокупности.

Считая, что потери от неправильной классификации одинаковы для любой пары 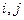, можно задачу классификации, т.е. отнесение наблюдения (объекта) неизвестной принадлежности 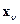к классу с номером 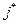, записать как

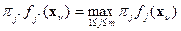(2.2)

Неизвестные величины в полученном правиле классификации рекомендуется заменить соответствующими оценками, полученными на базе обучающих выборок. Полагаем, что объединение всех обучающих совокупностей образует выборку объема 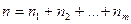из генеральной совокупности с законом распределения (2.1). Оценки получаются как частное от деления объема 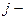ой обучающей выборки 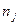на : .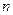

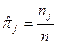Рассмотрим схему построения линейной дискриминантной функции, которая реализуется, когда каждый класс идентифицируется генеральной совокупностью с нормальным законом распределения. Т.е. в качестве функций 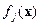используются 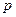-мерные нормальные плотности

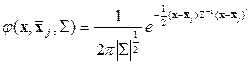, (2.3)

где 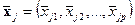- вектор-строка средних значений 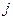-го класса, 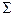- ковариационная матрица одинаковая для всех классов.

Неизвестные параметры заменяем оценками, которые определяются по данным обучающей выборки:

,

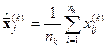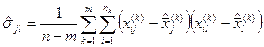
Как только получены оценки, их подставляют вместо неизвестных параметров в соответствующие функции 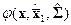и строят решающее правило. Особенно просто это правило выглядит в случае, когда распознаются только два класса, т.е. 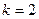. Для этого случая правило может быть записано в следующей эквивалентной форме:

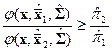
Или после логарифмирования

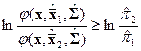
Учитывая, что 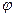является функцией нормальной плотности, т.е. имеет вид (2.3), полученное соотношение можно записать в следующем виде:

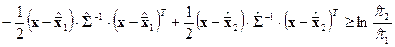
Предполагая далее, что априорные вероятности равны между собой, т.е. 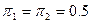, и, проведя соответствующее преобразование последнего выражения, окончательно получаем решающее правило

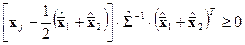
в соответствии с которым наблюдение 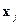следует отнести к первому классу, если неравенство выполняется, и ко второму – в противном случае. Из решающего правила можно получить формулу для расчета коэффициентов дискриминантной функции

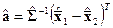
И применять для принятия решения не формулу, а полученную линейную функцию с коэффициентами .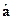

Пример 2.1. Владельцам компании ОАО «Спектр» принадлежит сеть супермаркетов. В 20ХХ г. Эта компания осуществляла торговую деятельность на территории 12 регионов страны. В стратегические планы компании следующего года входит расширение сети супермаркетов за счет освоения новых рынков сбыта в других регионах. Аналитиками компании были идентифицированы наиболее значимые для решаемой задачи показатели, характеризующие социально-экономическое развитие регионов. Такими показателями оказались:

1) общий объем товарооборота и платных услуг на душу населения (тыс. руб.), х₁;

2) объем инвестиций в основной капитал на душу населения (тыс. руб.), х₂;

3) коэффициент плотности автомобильных дорог, х₃;

4) соотношение среднедушевых доходов и среднедушевого прожиточного минимума, х₄.

Принимая во внимание тот факт, что в некоторых регионах компания имела положительный (долговременное получение прибыли) или негативный (терпела убытки) опыт свей деятельности, эти регионы были разделены, соответственно, на две группы. В результате была сформирована таблица.

Показатели, характеризующие уровень социально-экономического развития оставшихся регионов, на территории которых ОАО «Спектр» еще не осуществлял свою деятельность, но которые входят в круг его коммерческих интересов, представлены в табл. 2.2.

Таблица 2.1 - Показатели, характеризующие уровень социально-экономического развития регионов в 20ХХ г.

№	Регион	x1	x2	x3	x4
Группа регионов, в которых деятельность ОАО "Спектр" была успешной
1.	Луганская область	28,94	8,64	32,06	2,29
2.	Донецкая область	31,59	3,96	25,56	2,16
3.	Кировоградская область	23,63	6,33	30,05	1,79
4.	Киевская область	23,62	8,22	29,69	1,62
5.	Херсонская область	21,43	5,78	27,57	1,59
6.	Одесская область	17,62	4,62	24,62	1,57
7.	г. Киев	86,02	20,37	61,69	5,09
Группа регионов, в которых деятельность ОАО "Спектр" не была успешной
1.	Хмельницкая область	17,97	2,45	28,41	1,41
2.	Винницкая область	14,07	3,94	25,86	1,22
3.	Николаевская область	11,33	2,06	21,73	0,84
4.	Ивано - Франковская область	15,93	4,76	31,05	1,31
5.	Тернопольская область	20,18	2,8	25,92	1,53

Таблица 2.2 - Показатели, характеризующие уровень социально-экономического развития регионов, относительно которых необходимо принять маркетинговое решение

№	Регион	x1	x2	x3	x4
1.	Черновицкая область	17,47	5,97	28,17	1,29
2.	Львовская область	14,88	6,28	15,78	1,32
3.	Ровенская область	16,27	7,8	29,91	1,32
4.	Житомирская область	23,16	8,2	37,83	1,62
5.	Ужгородская область	15,39	6,82	41,28	1,11
6.	Черкасская область	19,28	9,68	27,79	1,82

Фактически задача состоит в получении прогнозных оценок в номинальной шкале, которые позволили бы без проведения полномасштабных полевых маркетинговых исследований предсказать успешность деятельности компании в регионах, указанных в табл. 2.2.

Решение задачи (используем MatLab). Классический дискриминантный анализ потребовал выполнения следующих шагов.

1. Ввод исходных данных и оформление их в виде матриц Х₁ , Х₂

>>X=dlmread('Пример31.txt')

X = 28.9400 8.6400 32.0600 2.2900 1.0000

31.5900 3.9600 25.5600 2.1600 1.0000

23.6300 6.3300 30.0500 1.7900 1.0000

23.6200 8.2200 29.6900 1.6200 1.0000

21.4300 5.7800 27.5700 1.5900 1.0000

17.6200 4.6200 24.6200 1.5700 1.0000

86.0200 20.3700 61.6900 5.0900 1.0000

17.9700 2.4500 28.4100 1.4100 0

14.0700 3.9400 25.8600 1.2200 0

11.3300 2.0600 21.7300 0.8400 0

15.9300 4.7600 31.0500 1.3100 0

20.1800 2.8000 25.9200 1.5300 0

>> X1=X(1:7,1:4)

X1 = 28.9400 8.6400 32.0600 2.2900

31.5900 3.9600 25.5600 2.1600

23.6300 6.3300 30.0500 1.7900

23.6200 8.2200 29.6900 1.6200

21.4300 5.7800 27.5700 1.5900

17.6200 4.6200 24.6200 1.5700

86.0200 20.3700 61.6900 5.0900

>> X2=X(8:12,1:4)

X2 = 17.9700 2.4500 28.4100 1.4100

14.0700 3.9400 25.8600 1.2200

11.3300 2.0600 21.7300 0.8400

15.9300 4.7600 31.0500 1.3100

20.1800 2.8000 25.9200 1.5300

2. Расчет векторов средних по каждой группе 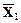и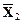

>> X1m=mean(X1)

X1m = 33.2643 8.2743 33.0343 2.3014

>> X2m=mean(X2)

X2m = 15.8960 3.2020 26.5940 1.2620

3. Определение оценок ковариационных матриц ,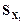

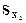
>> sx2=cov(X2)

sx2 = 11.7095 0.1595 6.1449 0.8651

0.1595 1.2508 2.7152 0.0767

6.1449 2.7152 11.9513 0.5964

0.8651 0.0767 0.5964 0.0690

>> sx1=cov(X1)

sx1 = 562.5490 124.9503 297.6310 29.7934

124.9503 31.4019 71.4771 6.6357

297.6310 71.4771 166.4522 15.8040

29.7934 6.6357 15.8040 1.5939

4. Расчет несмещенных оценок суммарной ковариационной матрицы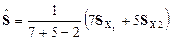

>> n1=size(X1,1)

n1 = 7

>> n2=size(X2,1)

n2 = 5

>> sx=1/(n1+n2-2)*(n1*sx1+n2*sx2)

sx = 399.6390 87.5450 211.4142 21.2879

87.5450 22.6068 51.3916 4.6834

211.4142 51.3916 122.4922 11.3610

21.2879 4.6834 11.3610 1.1502

5. Нахождение матрицы, обратной к суммарной ковариационной матрице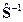

>> sx1=inv(sx)

sx1 = 0.1843 -0.0555 0.0072 -3.2553

-0.0555 1.0436 -0.5151 1.8650

0.0072 -0.5151 0.3538 -1.5297

-3.2553 1.8650 -1.5297 68.6332

6. Определение векторов оценок коэффициентов дискриминации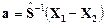

>> a=sx1*(X1m'-X2m');

a’ = -0.4185 2.9512 -1.7997 14.4091

7. Вычисление значений дискриминантных функций для каждого наблюдения выборочных совокупносте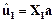й и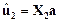

>> u1=X1*a;

u1’ = -11.3149 -16.4106 -19.4971 -15.7168 -18.6181 -15.4260 -13.565

>> u2=X2*a;

u2’ = -31.1029 -23.2220 -25.6662 -29.6240 -24.7845

8. Нахождение средних для полученных значений дискриминантных функций

>> u1m=mean(u1)

u1m = -15.7927

>> u2m=mean(u2)

u2m = -26.8799

9. Получение константы

>> c=(u1m+u2m)/2

c = -21.3363

10. Идентификация регионов, данные по которым представлены в табл. 3.2.

>> load X3.txt

X3 = 17.4700 5.9700 28.1700 1.2900

14.8800 6.2800 15.7800 1.3200

16.2700 7.8000 29.9100 1.3200

23.1600 8.2000 37.8300 1.6200

15.3900 6.8200 41.2800 1.1100

19.2800 9.6800 27.7900 1.8200

>> u3=X3*a;

u3’ = -21.8026 2.9268 -18.5989 -30.2329 -44.6114 -3.2905

Таблица 2.3 - Результаты дискриминантного анализа

№	Регион		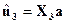Вывод о принадлежности регионов к группе
1.	Черновицкая область	-28,604	2 группа
2.	Львовская область	-19,948	1 группа
3.	Ровенская область	-24,674	1 группа
4.	Житомирская область	-39,487	2 группа
5.	Ужгородская область	-58,016	2 группа
6.	Черкасская область	-5,197	1 группа

Первую группу составляют регионы, на территории которых деятельность компании ожидается успешной, вторая группа – менее привлекательные регионы.

Классификация дискриминантным анализом может быть выполнена встроенной функцией MatLab, входящей в состав Stastistic Toolbox:

class = classify(sample,training,group,' type ')

Относит каждую строку данных из sampleк одной из групп.

training - обучающая выборка, матрица Х

.

Матрицы sample и training должны иметь одинаковое число столбцов.

group - определяет к какому классу относится каждая из записей в training.

Параметр type задается в одинарных кавычках и может принимать одно из следующих значений:

· linear — предполагает многомерное нормальное распределение для каждой группы с одинаковой ковариацией. Полагается по умолчанию.

· diaglinear — похоже на linear, но с диагональной матрицей ковариации (наивный Байесовский классификатор).

· quadratic — предполагает многомерное нормальное распределение для каждой группы.

· diagquadratic — похоже на quadratic, но с диагональной матрицей ковариаций (наивный Байесовский классификатор).

· mahalanobis — использует расстояние Махаланобиса.

Используем эту функцию для решения предыдущего примера:

X=dlmread('Пример31.txt')

>> load X3.txt

>> c = classify(X3,X(:,1:4),X(:,5))

c = 0 1 1 0 0 1

с – полученный вектор классов для данных из таблицы 2.2 и вполне согласуется с результатами, приведенными в таблице 2.3.

Пример 2.2. Решить задачу об ирисах, предложенную Р.Фишером в 1936 году. По известным значениям четырех признаков цветка необходимо отнести ирис к одному из трех классов: 1 – Iris Setosa, 2 – Iris Versicolor; 3 – Iris Virginica. Признаками ирисов, которые используются для принятия решения, являются: x1 – длина чашелистика; x2 – ширина чашелистика; x3 – длина лепестка; x4 – ширина лепестка. Имеются данные измерений для 150 экземпляров ирисов, в равных частях (по 50 штук) принадлежащих к трем видам (iris setosa, iris versicolor, iris virginica). Входной файл состоит из 150 строк (по 50 для каждого сорта).

Таблица 2.4 – Фрагмент исходных данных к задаче

Длина чашелистика	Ширина чашелистика	Длина лепестка	Ширина лепестка	Класс
5.1	3.5	1.4	0.2	Setosa
4.9	3.0	1.4	0.2	Setosa
4.7	3.2	1.3	0.2	Setosa
4.6	3.1	1.5	0.2	Setosa
5.0	3.6	1.4	0.2	Setosa
5.4	3.9	1.7	0.4	Setosa
4.6	3.4	1.4	0.3	Setosa

Загрузим исходные данные. В массиве meas(150,4) помещаются данные об измерениях, а в массиве species - соответствующие метки классов. Покажем как различные виды ирисов отличаются по измерениям. Используем первые 2 измерения.>> load fisheriris>> gscatter(meas(:,1), meas(:,2), species,'rgb','osd');>> xlabel('Sepal length');>>ylabel('Sepal width');>>N = size(meas,1);

Функия scatter(x,y,group) создает точечную диаграмму от x и y, сгруппированную по переменной group, которая является меткой класса или категориальной переменной.

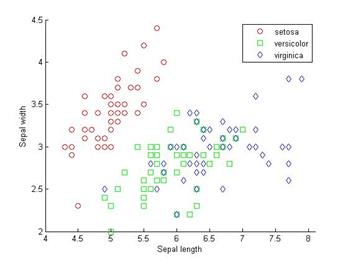
Рисунок 2.2 – Распределение точек для разных классов

Выполним классификацию линейным дискриминантным анализом

ldaClass = classify(meas(:,1:2),meas(:,1:2),species);

Вычислим ошибку дискриминации на обучающем множестве

bad = ~strcmp(ldaClass,species);ldaResubErr = sum(bad) / NldaResubErr = 0.2000

Можно также вычислить матрицу сопряженности для полученного решения.

[ldaResubCM,grpOrder] = confusionmat(species,ldaClass)ldaResubCM = 49 1 0 0 36 14 0 15 35grpOrder = 'setosa' 'versicolor' 'virginica'

Из 150 наблюдений 20% или 30 значений классифицированы неправильно. Отметим на графике крестиками неправильно классифицированные ирисы.

hold on;

plot(meas(bad,1), meas(bad,2), 'kx');

hold off;

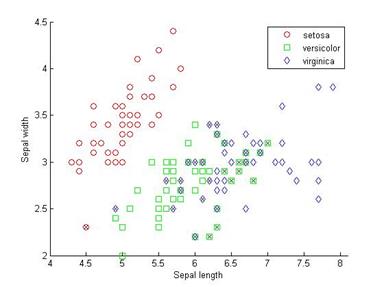
Рисунок 2.3 – Результаты классификации ирисов

Линейный дискриминантный анализ делит плоскость на области прямыми линиями и назначает разным областям разные виды ирисов. Чтобы показать эти области построим сетку значений (x,y) и применим функцию классификации к сетке.

[x,y] = meshgrid(4:.1:8,2:.1:4.5);x = x(:); y = y(:);j = classify([x y],meas(:,1:2),species);gscatter(x,y,j,'grb','sod')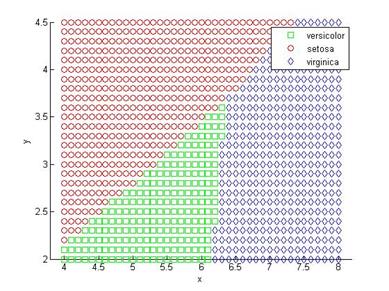

Рисунок 2.4 – Разделение плоскости функцией классификации

Для части данных области различных классов не разделимы линейно. В этом случае линейный дискриминантный анализ непремлем. Вместо этого попробуем применить квадратичный дискриминантный анализ.

qdaClass = classify(meas(:,1:2),meas(:,1:2),species,'quadratic');bad = ~strcmp(qdaClass,species);qdaResubErr = sum(bad) / NqdaResubErr = 0.2000

Последнее значение показывает ошибку классификации на обучающем множестве. Обычно более интересной является ошибка на тестовых данных, которая является оценкой ожидаемой ошибки на новом независимим множестве.

В случае, когда не имеется другого множества данных, его моделируют, используя перекрестную проверку или кросс-валидацию. Наиболее популярным способом оценки ошибок классификации является 10-блочная кросс-валидация. Этот алгоритм случайным образом делит обучающее множество на 10 непересекающихся подмножеств, котрые имеют приблизительно равные размеры и приблизительно равные (как в обучающей выборке) пропорции классов.

Удаляем одно подмножество, обучаем модель на оставшихся 9-ти и вычисляем ошибку классификации на удаленном подмножестве. Повторяем процедуру удаления с каждым из 10 подмножеств. А полученную ошибку осредняем.

Поскольку кросс-валидация случайным образом делит данные, ее результаты зависят от начальных значений. Чтобы точно воспроизвести результаты примера, выполните следующие команды:

s = RandStream('mt19937ar','seed',0);RandStream.setDefaultStream(s);

Используем функцию cvpartition чтобы сгенерировать 10 непересекающихся подмножеств.

cp = cvpartition(species,'k',10)cp = K-fold cross validation partition N: 150 NumTestSets: 10 TrainSize: 135 135 135 135 135 135 135 135 135 135 TestSize: 15 15 15 15 15 15 15 15 15 15

Функция crossval может оценивать ошибки классификации как для LDA так и для QDA используя заданное разбиение cp.

Оценим ошибку на тестовых множествах для LDA, используя 10- блочную кросс-валидацию.

ldaClassFun= @(xtrain,ytrain,xtest)(classify(xtest,xtrain,ytrain));ldaCVErr = crossval('mcr',meas(:,1:2),species,'predfun',... ldaClassFun,'partition',cp)ldaCVErr = 0.2000

Ошибка кросс-валидации для LDA получилась та же, что и для обучающего множества.

Оценим ошибку на тестовых множествах для QDA, используя 10- блочную кросс-валидацию.

qdaClassFun = @(xtrain,ytrain,xtest)(classify(xtest,xtrain,ytrain,... 'quadratic'));qdaCVErr = crossval('mcr',meas(:,1:2),species,'predfun',... qdaClassFun,'partition',cp)qdaCVErr = 0.2267

QDA имеет несколько большую ошибку, чем LDA. Это говорит о том, что более простая модель является более приемлемой.

Задание для самостоятельной работы. Выполните классификацию ирисов по 4 измерениям, выполните кросс-валидацию и оцените ошибку.