Способы измерения влияния факторов в стохастическом факторном анализе

Для измерения влияния факторов в стохастическом анализе, когда взаимосвязь между показателями неполная, вероятностная используются приемы корреляционного анализа.

Необходимые условия применения корреляционного анализа:

1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике либо за один период, но по совокупности объектов).

2. Исследуемые факторы должны быть количественно измеримы и отражены в источниках информации.

Задачи, решаемые при применении корреляционного анализа:

- определение изменения результативного показателя под воздействием одного или нескольких факторов, т. е. определение на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу;

- установление относительной степени зависимости результативного показателя от каждого фактора.

Этапы корреляционного анализа:

1. Определение факторов, влияющих на результативный показатель и отбор более существенных. При этом необходимо придерживаться следующих правил:

- факторы должны находиться в причинно – следственной связи с результативным показателем;

- необходимо отбирать самые значимые факторы;

- в корреляционную модель не рекомендуется включать взаимосвязанные факторы – если парный коэффициент корреляции между факторами больше 0,85, то один из факторов необходимо исключить с целью избежания искажения результатов анализа;

- нежелательно включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер.

2. Сбор информации по каждому показателю. Она должна быть проверена на однородность и соответствие закону нормального распределения.

Критерием однородности информации служит коэффициент вариации. Значения коэффициента вариации: до 10% - вариация незначительна; 10 – 20 % - средняя; 20 – 33% - значительная; свыше 33% - информация неоднородна, поэтому для проведения анализа необходимо исключить нетипичные признаки.

3. Моделирование связи – т.е. подбор и обоснование математического уравнения, которое наиболее точно выражает сущность исследуемой зависимости. Для его обоснования служат те же приемы, что и для установления связи: аналитические группировки и линейные графики.

Может быть построено уравнение по прямой, степенной, логарифмической, параболической и другим функциям.

4. Расчет основных показателей корреляционного анализа: уравнения связи, коэффициентов корреляции, детерминации, эластичности. Решение задач многофакторного корреляционного анализа производится на ПЭВМ по типовым программам.

5. Статистическая оценка и практическое использование результатов корреляционного анализа. Для оценки надежности показателей связи используется критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации.

Дисперсионный анализ основан на расчете показателей дисперсии – среднего из квадратов отклонений значений изучаемых показателей от средней величины. Практическая значимость анализа обусловлена возможностью разложения показателя дисперсии на составные элементы, позволяющие оценить влияние различных факторов, вызывающих изменение изучаемого показателя (признака, явления).

Дискриминантный анализ является одним из методов многомерного стохастического анализа.

Цель дискриминантного анализа состоит в том, чтобы на основе измерения различных характеристик (параметров) объекта классифицировать его, то есть отнести к одной из нескольких групп (классов) оптимальным способом. Суть анализа: предположим, что имеется n объектов с m характеристиками. В результате измерений каждый объект характеризуется вектором характеристик 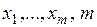>1. Задача состоит в том, чтобы по результатам измерений отнести объект к одной из нескольких групп (классов) 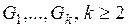. Иными словами, нужно построить решающее правило, позволяющее по результатам измерений параметров объекта указать группу, к которой он принадлежит. Число групп заранее известно, также известно, что объект заведомо принадлежит к определенной группе.

Таким образом, корреляционный, дисперсионный и дискриминантный анализ имеет большую научную и практическую значимость. Это проявляется в том, что значительно углубляется факторный анализ, устанавливается место и роль каждого фактора в формировании уровня исследуемых показателей и как результат – точнее обосновываются планы и управленческие решения, объективнее оцениваются итоги деятельности предприятия и полнее определяются внутрихозяйственные резервы.