Сокращение размерности

3.3.1 Метод главных компонент позволяет заменить большое количество информации, основанной на взаимно коррелирующих входных данных, множеством статистически независимых компонентов с учетом их важности. Имеем матрицу наблюдений независимой переменной (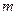 переменных, 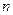наблюдений):

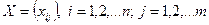
Согласно методу главных компонент вычисляем ковариационную матрицу для матрицы Х: 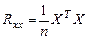размерность которой .

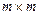Затем вычисляем 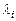- собственные числа ковариационной матрицы и соответствующие им собственные вектора 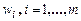. Собственные векторы и собственные значения связаны зависимостью:

,

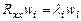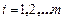
Собственные значения симметричной неотрицательной матрицы являются рациональными и неотрицательными. Упорядочим их в порядке убывания: 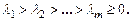В аналогичной последовательности расположим собственные векторы 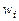, сопряженные с 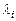. Если ограничиться 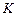максимальными собственными значениями, матрица W преобразования PCA (главных компонент) может быть определена в форме 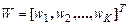, при 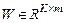. Эта матрица определяет преобразование РСА как линейное преобразование

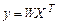
Вектор 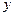представляет собой вектор главных компонент, имеющих наибольшее влияние на реконструкцию вектора данных Х.

Реконструкция Х на основе вектора 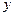и ортогональной матрицы 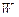проводится в соответствии с выражением

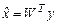
Представление вектора Х наибольшими главными компонентами 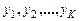, составляющими вектор 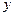, равнозначно сохранению информации о наибольшей части энергии, содержащейся во множестве данных. Первый (наибольший) главный компонент, сопряженный с 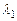своим собственным вектором 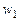, определяет направление в многомерном пространстве, в котором вариация данных максимальна.

В системе MatLab вычислить собственные числа и соответствующие им собственные вектора можно с помощью функции [V,D]=eig(A), где V – матрица собственных векторов, а D – матрица, у которой на диагонали стоят собственные числа. Обычно собственные числа расположены по возрастанию, поэтому выбираем несколько последних собственных векторов и формируем из них матрицу преобразования 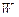. Вычисляем на основании этой матрицы и матрицы нормированных данных Х матрицу 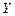- строки которой – главные компоненты, а столбцы – исходные данные для обучающей и тестирующей выборок нейронной сети.

В программе Deductor метод главных компонент реализован в пункте обработки данных – «Факторный анализ».