Приток упругой жидкости к галерее при постоянном перепаде давлений

Пусть в полубесконечном горизонтальном пласте постоянной толщины h и ширины В начальное пластовое давление всюду постоянно и равно p_k. На галерее (при х = 0) давление мгновенно снижено до р_г и в дальнейшем поддерживается постоянным (т. е. р_г = const(t)). В бесконечно удаленной точке (х –> ∞) давление в любой момент времени остается равным p_k. С течением времени давление в пласте изменяется p(x,t).

Рис. 1.1. Схема притока к галереи с постоянным давлением

В пласте образуется неустановившийся плоскопараллельный поток упругой жидкости. Давление в любой точке потока х и в любой момент времени t можно определить, интегрируя уравнение Фурье (1.14), которое для такого потока будет иметь вид

.

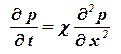(1.17)

Начальные и граничные условия при этом будут следующие:

р(х, 0) = pk; р(0, t) = рг; р(∞, t) = pk.

(1.18)

Задача заключается в определении дебита галереи Q(t) и давления в любой точке потока и в любой момент момент времени р(х, t).

Используя анализ размерностей, покажем, что поставленная задача автомодельная, т.е. из аргументов, от которых зависит давление, можно составить один (безразмерный) комплекс.

Обозначим через φ = (р - р_г)/(p_k - р_г) безразмерное давление, которое, как следует из соотношений (1.17) и (1.18), зависит от времени t, координаты х и коэффициента пьезопроводности χ, т. е. φ = f(x, t, χ).

Размерности этих аргументов таковы: [х] = L, [t] = T, [ χ ] = L²/T, и из них можно составить один безразмерный комплекс 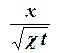. Приняв за новую переменную величину 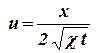сведем задачу к нахождению безразмерного давления φ, зависящего только от φ = f(u). При этом начальные и граничные условия переходят в следующие:

t = 0, u = ∞, φ(∞) = 1; x = 0, u = 0, φ(0) = 0; x = ∞, u = ∞, φ(∞) = 1;

(1.19)

В силу линейности дифференциального уравнения (1.15) для функции φ имеем такое же уравнение

.

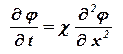(1.20)

По правилу дифференцирования сложных функций находим

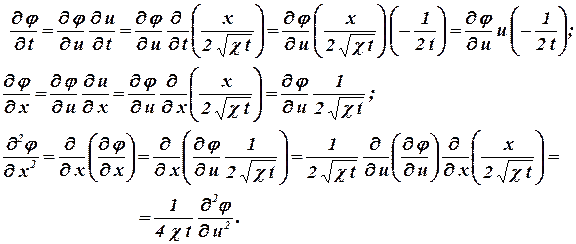(1.21)

Подставляя найденные значения производных в уравнение (1.20) получим обыкновенное дифференциальное уравнение

,

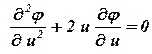(1.22)

которое должно быть решено при условиях (1.18). Для решения уравнения (1.20) обозначим 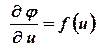, тогда уравнение (1.20) принимает вид

,

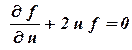(1.23)

Разделяя переменные в (1.23) и интегрируя, получаем

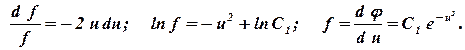(1.24)

где С₁ — постоянная интегрирования. Интегрируя (1.24), будем иметь

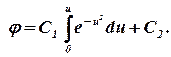(1.25)

Первое граничное условие (φ = 0 при u = 0) позволяет определить C₂ = 0.

Второе граничное условие и начальное условие одинаковы и позволяют определить С₁.

,

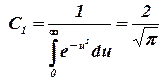(1.26)

Тогда

,

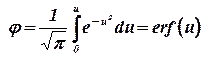(1.27)

Интеграл в (1.27) называется интегралом вероятности и является табулированной функцией, изменяющейся в пределах от 0 до 1.

Поэтому закон распределения давления в неустановившемся плоскопараллельном фильтрационном потоке упругой жидкости имеет вид

.

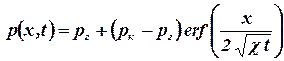(1.28)

Типичные кривые распределения давления в различные моменты времени в неустановившемся плоскопараллельном потоке упругой жидкости к галерее, пущенной в эксплуатацию с постоянным забойным давлением р_г = const, показаны на рис.??.1. На рисунке??.3 показано изменение давления в различных точках пласта с течением времени.

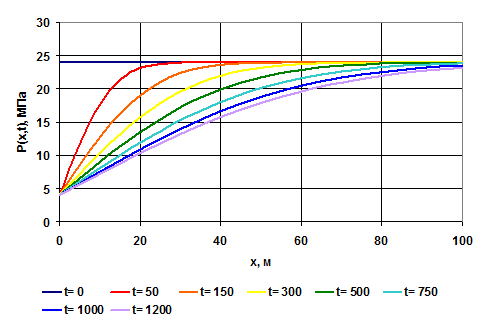Рис. 1.2. Кривые распределения давления по длине галереи в различные моменты

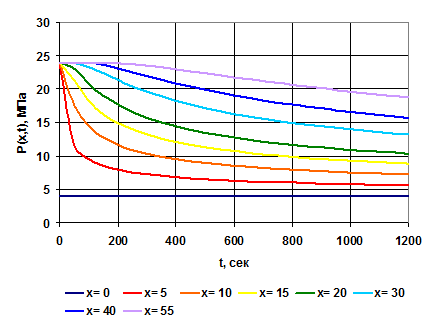Рис. 1.3. Изменение давления в различных точках галереи с течением времени

Найдем дебит галереи Q. Будем считать положительным дебит, отбираемый из галереи (х = 0, см. рис. 1.1), когда поток движется против оси 0x.

Согласно закону Дарси, имеем

,

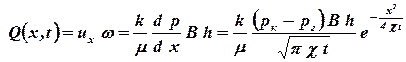(1.29)

где В, h — соответственно ширина и толщина пласта.

Типичные кривые распределения дебита в различные моменты времени в неустановившемся плоскопараллельном потоке упругой жидкости к галерее, пущенной в эксплуатацию с постоянным забойным давлением р_г = const, показаны на рис. 1.4. На рисунке 1.5 показано изменение давления в различных точках пласта с течением времени.

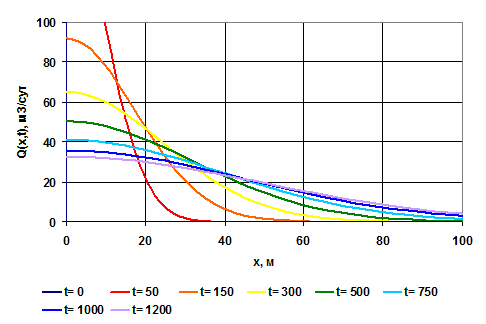Рис. 1.4. Кривые распределения дебита по длине галереи в различные моменты

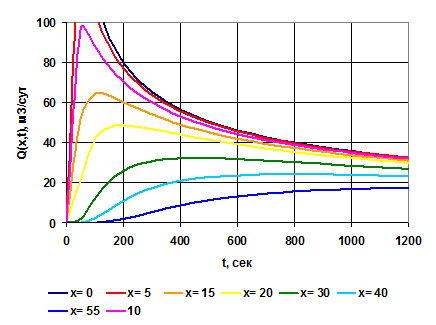Рис. 1.5. Изменение дебита в различных точках галереи с течением времени

Из формулы (1.29) следует, что дебит галереи убывает с течением времени как 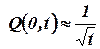и при t →∞ стремится к нулю. В начальный момент времени дебит равненравен бесконечности, что является следствием скачка давления на галерее в этот момент времени.