Виды регрессий.
1. Линейный одномерный случай
y = a0+ a1x
2. Параболическая или степенная регрессия 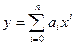
 3. Линейная множественная регрессия
3. Линейная множественная регрессия 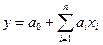
x1,...,xn y


факторы функция отклика
y(a,x) = a0+ a1x1+...+ anxn+ an+1x12+...+ a2nxn2+ a2n+1x1x2+...+ akxn-1xn
k+1 = (n+1)(n+2)/2
- число неизвестных 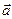 =?.
=?.
МНК имеет три этапа:
1 этап Определение коэффициентов а.
2 этап Оценка достоверности коэффициентов а.
3 этап Проверка адекватности модели.
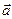 = (a0...ak)¢ - вектор- столбец
= (a0...ak)¢ - вектор- столбец
x = (x1...xk)¢ - вектор- столбец
f(x) = (1, x1,.., xk)¢
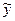 - наблюдаемые значения,
- наблюдаемые значения, 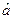 – оценки,
– оценки, 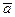 - истинные значения
- истинные значения
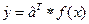
Эксперимент проводится в N точках, т.о. фиксируем x и y. x1, x2,..., xN - точки экспериментов.
xi= (xi1, xi2,..., xin)¢ 1 £ i £ N
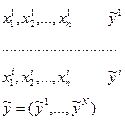 - вектор наблюдений функции отклика.
- вектор наблюдений функции отклика.
Для оценки адекватности модели в любой точке xi эксперимент повторяется n раз.
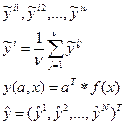
Информационная матрица
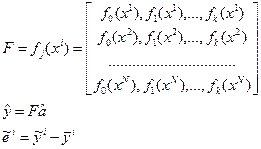
- ошибка, погрешность.
Требуемые условия.
1. Результаты наблюдений свободны от систематических ошибок
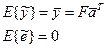
E - математическое ожидание.
2. Результат наблюдений в точке xj не зависит от результата наблюдений в точке xi.
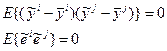
3. Дисперсия результатов наблюдений во всех точках одинакова.
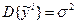 для любых i.
для любых i.
4. Оценка 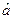 является несмещенной
является несмещенной
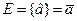
5. Дисперсия оценки 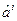 должна быть минимальна
должна быть минимальна
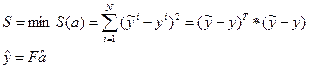
где 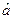 - оценка, которая еще пока не найдена.
- оценка, которая еще пока не найдена.
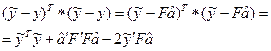
Так как ¶S/¶a = 0 то 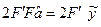 следовательно
следовательно 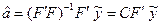

 xi
xi 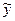
7.Матричная форма МНК при построении модели (этап проверки значимости коэффициентов модели).
Виды регрессий.
1. Линейный одномерный случай
y = a0+ a1x
2. Параболическая или степенная регрессия 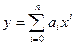
 3. Линейная множественная регрессия
3. Линейная множественная регрессия 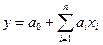
x1,...,xn y


факторы функция отклика
y(a,x) = a0+ a1x1+...+ anxn+ an+1x12+...+ a2nxn2+ a2n+1x1x2+...+ akxn-1xn
k+1 = (n+1)(n+2)/2
- число неизвестных 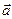 =?.
=?.
МНК имеет три этапа:
1 этап Определение коэффициентов а.
2 этап Оценка достоверности коэффициентов а.
3 этап Проверка адекватности модели.
Ошибка оценивания.
Реально 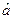 отличается от
отличается от 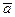 . Дисперсия - мера отличия. Чем больше дисперсия, тем больше отличие. Дисперсия будет зависеть как от дисперсии ошибок наблюдения σ2, так и от точек постановки опытов.
. Дисперсия - мера отличия. Чем больше дисперсия, тем больше отличие. Дисперсия будет зависеть как от дисперсии ошибок наблюдения σ2, так и от точек постановки опытов.
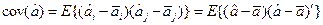
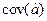 - ковариационная матрица.
- ковариационная матрица.
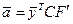
Поставим вместо а ее оценку и с учетом условий запишем все необходимые выражения.
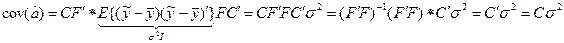
Так как корреляционная матрица симметрична, то при
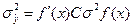 - дисперсия коэффициента аi
- дисперсия коэффициента аi
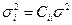
Действует нормальный закон распределения.
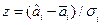 - стандартное отклонение
- стандартное отклонение
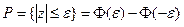 , где Ф(ε) – функция Лапласа
, где Ф(ε) – функция Лапласа
α→Р→ε
α – уровень значимости (0,1;0,05;0,01)
1-α=Р
Р-вероятность,ε – из таблицы интегралов
Пусть Р=0,95, следовательно ε=1,96
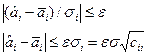
, где σ2- дисперсия ошибки наблюдения.
Если σ2задана, то 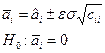
Если 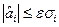 , то Н0имеет место (не отвергается)
, то Н0имеет место (не отвергается)
Рассмотрим случай, когда неизвестна дисперсия наблюдения s2
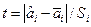 Si- оценка si
Si- оценка si
Распределение Стьюдента похоже на нормальный закон распределения. 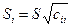
S2- аналог s2
Si- аналог si
S2-эмпирическая дисперсия
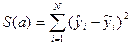
j= N - (k+1) - число степеней свободы
N - число опытов, (k+1) - число формул
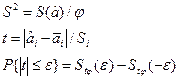
Stj(e) и Stj(-e) - из таблицы Стьюдента
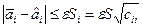
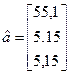 y = a0+ a1x1 + a2x2
y = a0+ a1x1 + a2x2
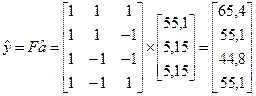
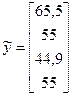
S2= SR/j = 4*0,01/(4-3) = 0,04 где в знаменателе 4 - число опытов, и 3 - число коэффициентов.
отсюда S = 0,2
C = (F¢F)-1= (1/4)*I3
где I3- единичная матрица 3-го порядка.
Si= 0,2Ö1/4 = 0,1
Пусть
a = 0,1 ® P = 0,9 ® e = 6,3
тогда 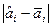 £ 6,3*0,1 = 0,63;
£ 6,3*0,1 = 0,63; 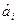 > eSi = 0,63;
> eSi = 0,63; 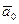 = 55,1 ± 0,6;
= 55,1 ± 0,6; 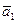 = 5,15 ± 0,63;
= 5,15 ± 0,63; 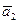 = 5,15 ± 0,63
= 5,15 ± 0,63
8.Матричная форма МНК при построении модели (этап проверки адекватности полученной модели).
Виды регрессий.
1. Линейный одномерный случай
y = a0+ a1x
2. Параболическая или степенная регрессия 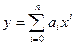
 3. Линейная множественная регрессия
3. Линейная множественная регрессия 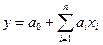
x1,...,xn y


факторы функция отклика
y(a,x) = a0+ a1x1+...+ anxn+ an+1x12+...+ a2nxn2+ a2n+1x1x2+...+ akxn-1xn
k+1 = (n+1)(n+2)/2
- число неизвестных 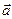 =?.
=?.
МНК имеет три этапа:
1 этап Определение коэффициентов а.
2 этап Оценка достоверности коэффициентов а.
3 этап Проверка адекватности модели.
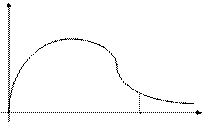 Проверка адекватности модели.
Проверка адекватности модели.
Н0: tр£ tкр
где tр- расчетное значение; tкр- табличное значение
1- a = р
a
В основе проверки адекватности модели лежит сопоставление достигнутой точности модели с точностью наблюдения. Для оценки точности используем дисперсию, поэтому необходимо сравнить дисперсию ошибки по модели с дисперсией ошибки наблюдений. Поэтому в каждой точке эксперимент повторяется n раз.
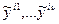 отсюда следует, что
отсюда следует, что 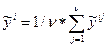
1.Дисперсия ошибки моделирования. 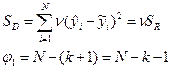
2. Дисперсия ошибки наблюдения 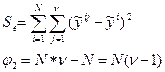
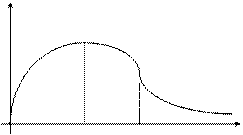 Далее рассчитываем статистику Фишера Fр= (SD/j1)/(Se/j2). Если ошибка моделирования меньше ошибки наблюдения, то модель хорошая. Выдвигается гипотеза Н0. Определяется уровень значимости a.
Далее рассчитываем статистику Фишера Fр= (SD/j1)/(Se/j2). Если ошибка моделирования меньше ошибки наблюдения, то модель хорошая. Выдвигается гипотеза Н0. Определяется уровень значимости a.
В соответствии с a, j1и j2из таблицы находим Fкр.
P{ïFï < Fкр} = 1-a
fF
F
Fp Fкр
Если Fp£ Fкр, то модель адекватна.
 2015-05-13
2015-05-13 920
920








