Типовой расчет
Указания к оформлению типового расчета
Типовой расчет состоит из 5 задач, для каждой из которых разработано 30 вариантов. Номер варианта, сроки выполнения задания в целом и каждой задачи в отдельности, а так же срок защиты устанавливаются для студента преподавателем, ведущим в группе практические занятия по математике.
Расчетно-пояснительный текст работы выполняется на отдельных листах формата А4 черной или синей пастой с полями шириной 2 см. По окончании работы листы брошюруются.
В центре титульного листа должна быть помещена надпись следующего содержания:
Типовой расчет
Приложения дифференциального исчисления
функции одной переменной
студента группы ________
Фамилия, имя, отчество
20___ – 20___ учебный год
В конце расчетно-пояснительной части указывается список используемой литературы, дата окончания работы и роспись студента.
Рассмотрение каждой задачи начинается с новой страницы. Задачи располагаются в порядке следования номеров. Решению задачи должно предшествовать условие, которое формулируется не в том общем виде, как в задании, а уже применительно к варианту, по которому работает студент.
Все математические преобразования должны быть достаточно подробными и сопровождаться краткими пояснениями, записи – аккуратными и грамотными.
При выполнении чертежей должны быть использованы необходимые чертежные инструменты и принадлежности. Оси системы координат, графики функций вычерчиваются сплошной линией. Все другие вспомогательные линии наносятся на чертеж пунктиром.
Студенту, приступающему к выполнению задания, полезно ознакомиться с образцом решения задач.
При защите работы студент должен уметь отвечать на теоретические вопросы и пояснять приведенные им решения задач.
При невыполнении требований по оформлению работы преподаватель вправе отказать студенту в приеме работы на проверку и потребовать правильного оформления работы!
Типовые задания
Задача № 1. Найдите производную 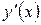 данных функций
данных функций
| вари ант | y = f (x) |
а) 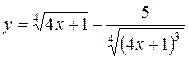 ; б) ; б) 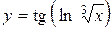 ; в) ; в) 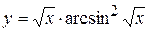 ;
г) ;
г) 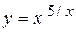 ; д) ; д) 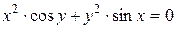 , е) , е) 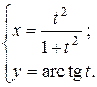
| |
а) 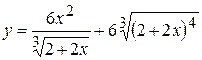 ; б) ; б) 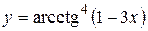 ; в) ; в) 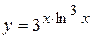 ;
г) ;
г) 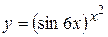 ; д) ; д) 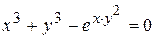 , е) , е) 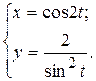
| |
а) 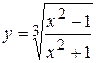 ; б) ; б) 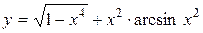 ; в) ; в) 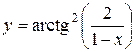 ;
г) ;
г) 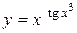 ; д) ; д) 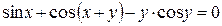 , е) , е) 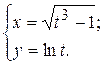
| |
а) 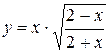 ; б) ; б) 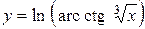 ; в) ; в) 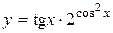 ;
г) ;
г) 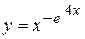 ; д) ; д) 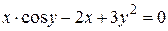 , е) , е) 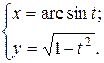
| |
а) 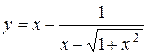 ; б) ; б) 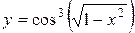 ; в) ; в) 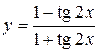 ;
г) ;
г) 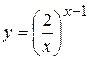 ; д) ; д) 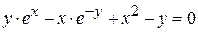 , е) , е) 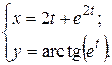
| |
а) 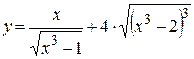 ; б) ; б) 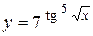 ; в) ; в) 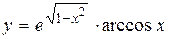 ;
г) ;
г) 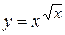 ; д) ; д) 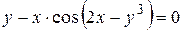 , е) , е) 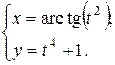
|
| вари ант | y = f (x) |
а) 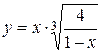 ; б) ; б) 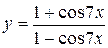 ; в) ; в) 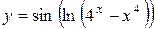 ;
г) ;
г) 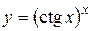 ; д) ; д) 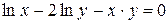 , е) , е) 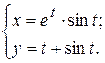
| |
а) 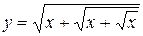 ; б) ; б) 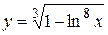 ; в) ; в) 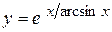 ;
г) ;
г) 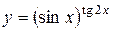 ; д) ; д) 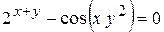 , е) , е) 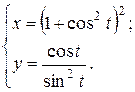
| |
а) 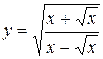 ; б) ; б) 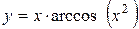 ; в) ; в) 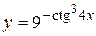 ;
г) ;
г) 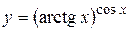 ; д) ; д) 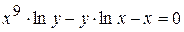 , е) , е) 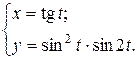
| |
а) 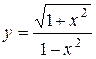 ; б) ; б) 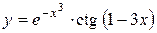 ; в) ; в) 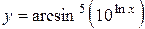 ;
г) ;
г) 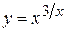 ; д) ; д) 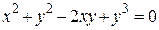 , е) , е) 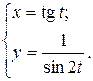
| |
а) 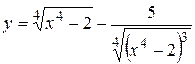 ; б) ; б) 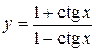 ; в) ; в) 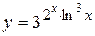 г)
г) 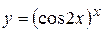 ; д) ; д) 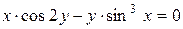 , е) , е) 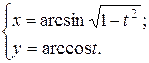
| |
а) 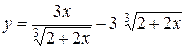 ; б) ; б) 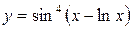 ; в) ; в) 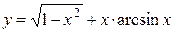 ;
г) ;
г) 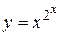 ; д) ; д) 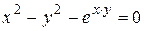 , е) , е) 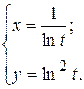
| |
а) 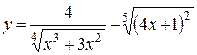 ; б) ; б) 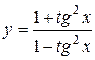 ; в) ; в) 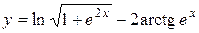 ;
г) ;
г) 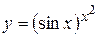 ; д) ; д) 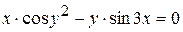 , е) , е) 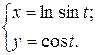
|
| вари ант | y = f (x) |
а) 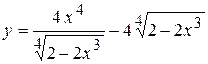 ; б) ; б) 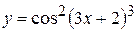 ; в) ; в) 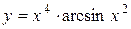 ;
г) ;
г) 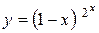 ; д) ; д) 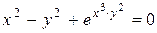 , е) , е) 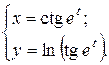
| |
а) 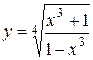 ; б) ; б) 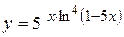 ; в) ; в) 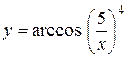 ;
г) ;
г) 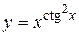 ; д) ; д) 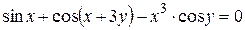 , е) , е) 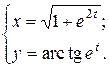
| |
а) 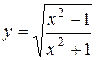 ; б) ; б) 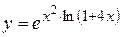 ; в) ; в) 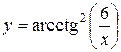 ;
г) ;
г) 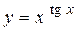 ; д) ; д) 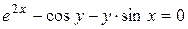 е) е) 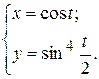
| |
а) 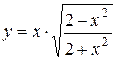 ; б) ; б) 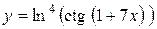 ; в) ; в) 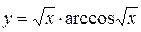 ;
г) ;
г) 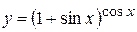 ; д) ; д) 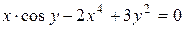 , е) , е) 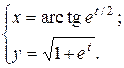
| |
а) 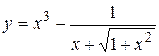 ; б) ; б) 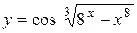 ; в) ; в) 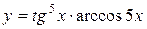 ;
г) ;
г) 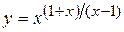 ; д) ; д) 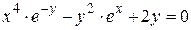 , е) , е) 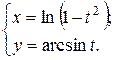
| |
а) 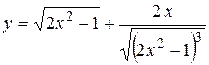 ; б) ; б) 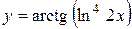 ; в) ; в) 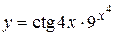 ;
г) ;
г) 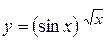 ; д) ; д) 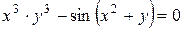 , е) , е) 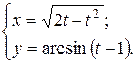
| |
а) 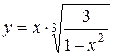 ; б) ; б) 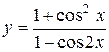 ; в) ; в) 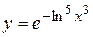 ;
г) ;
г) 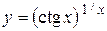 ; д) ; д) 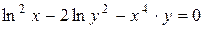 , е) , е) 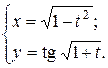
| |
| вари ант | y = f (x) |
а) 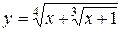 ; б) ; б) 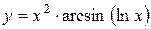 ; в) ; в) 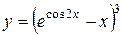 ;
г) ;
г) 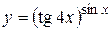 ; д) ; д) 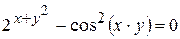 , е) , е) 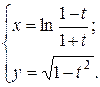
| |
а) 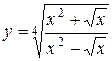 ; б) ; б) 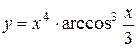 ; в) ; в) 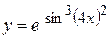 ;
г) ;
г) 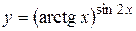 ; д) ; д) 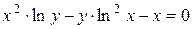 , е) , е) 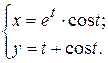
| |
а) 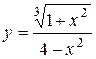 ; б) ; б) 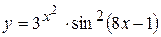 ; в) ; в) 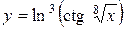 ;
г) ;
г) 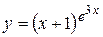 ; д) ; д) 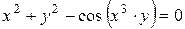 , е) , е) 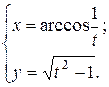
| |
а) 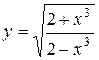 ; б) ; б) 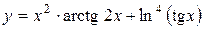 ; в) ; в) 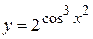 ;
г) ;
г) 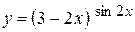 ; д) ; д) 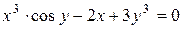 , е) , е) 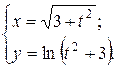
| |
а) 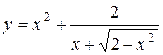 ; б) ; б) 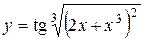 ; в) ; в) 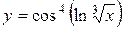 ;
г) ;
г) 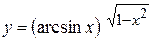 ; д) ; д) 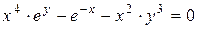 , е) , е) 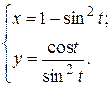
| |
а) 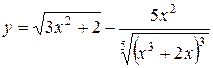 ; б) ; б) 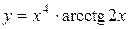 ; в) ; в) 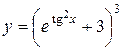 ;
г) ;
г) 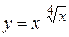 ; д) ; д) 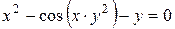 , е) , е) 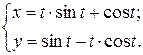
|
| вари ант | y = f (x) |
а) 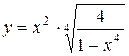 ; б) ; б) 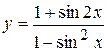 ; в) ; в) 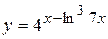 ;
г) ;
г) 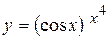 ; д) ; д) 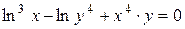 , е) , е) 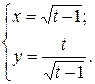
| |
а) 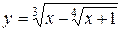 ; б) ; б) 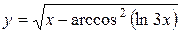 ; в) ; в) 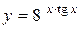 ;
г) ;
г) 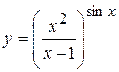 ; д) ; д) 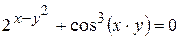 , е) , е) 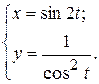
| |
а) 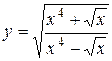 ; б) ; б) 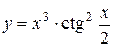 ; в) ; в) 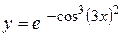 ;
г) ;
г) 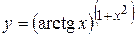 ; д) ; д) 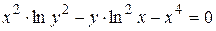 , е) , е) 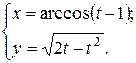
| |
а) 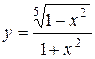 ; б) ; б) 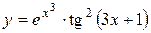 ; в) ; в) 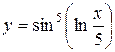 ;
г) ;
г) 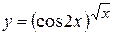 ; д) ; д) 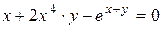 , е) , е) 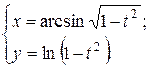
|
Задача № 2. Составьте формулу Тейлора для данной функции y = f (x) в точке х = а с остаточным членом в форме Лагранжа.
| № варианта | y = f (x) | а | № варианта | y = f (x) | а |
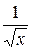
| 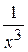
| -1 | |||
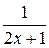
| -1 | 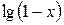
| |||
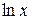
| 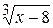
| ||||
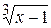
| 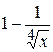
| ||||
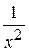
| 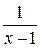
| -3 | |||
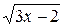
| 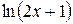
| ||||
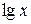
| 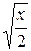
| ||||
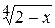
| 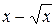
| ||||
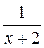
| 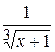
| ||||
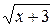
| 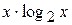
| ||||
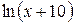
| -9 | 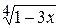
| |||
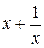
| -1 | 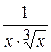
| -1 | ||
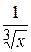
| -8 | 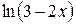
| |||
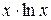
| 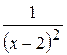
| ||||
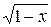
| 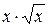
|
Задача № 3. Найдите наибольшее и наименьшее значения функции y = f (x) на отрезке [ a, b ]. (№ – номер варианта).
| № | y = f (x) | [ a, b ] | № | y = f (x) | [ a, b ] |
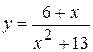
| [-5, 5] | 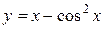
| 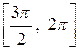
| ||
| y =0,5 x +cos x | 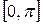
| 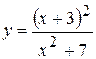
| [-3, 7] | ||
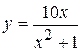
| [0, 3] | 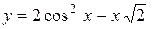
| 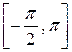
| ||
| y = 0,5 x –sin x | 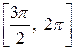
| 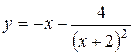
| [-1, 4] | ||
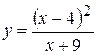
| [-4, 6] | 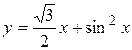
| 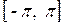
| ||
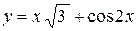
| 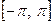
| 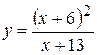
| [-1, 7] | ||
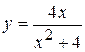
| [-5, 1] | 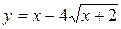
| [-2, 5] | ||
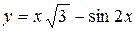
| 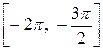
| 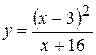
| [-5, 5] | ||
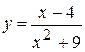
| [-4, 6] | 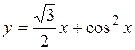
| 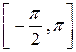
| ||
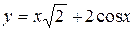
| 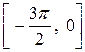
| 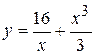
| [-1, 3] | ||
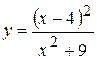
| [3, 6] | 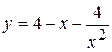
| [1, 4] | ||
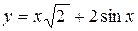
| 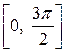
| 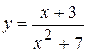
| [-3, 7] | ||
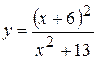
| [-5, 5] | 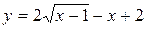
| [1, 5] | ||
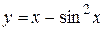
| 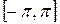
| 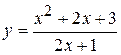
| [0, 4] | ||
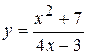
| [1, 5] | 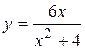
| [-1, 4] |
Задача № 4. Проведите полное исследование функций y = f 1(x), y = f 2(x) и y = f 3(x). Постройте график.
| Вариант | y = f 1(x) | y = f 2(x) | y = f 3(x) |
| 1. | 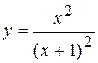
| 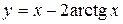
| 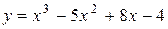
|
| 2. | 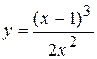
| 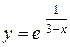
| 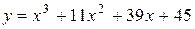
|
| 3. | 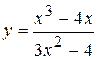
| 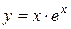
| 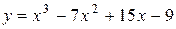
|
| 4. | 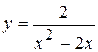
| 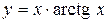
| 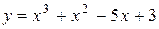
|
| 5. | 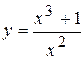
| 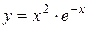
| 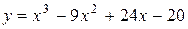
|
| 6. | 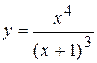
| 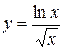
| 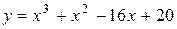
|
| 7. | 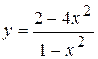
| 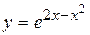
| 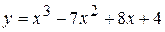
|
| 8. | 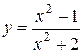
| 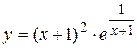
| 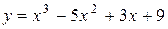
|
| 9. | 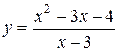
| 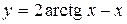
| 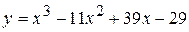
|
| 10. | 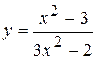
| 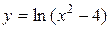
| 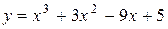
|
| 11. | 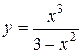
| 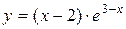
| 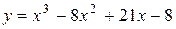
|
| 12. | 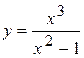
| 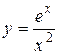
| 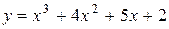
|
| 13. | 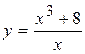
| 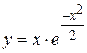
| 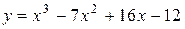
|
| 14. | 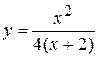
| 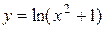
| 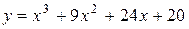
|
| 15. | 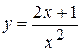
| 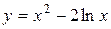
| 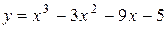
|
| Вариант | y = f 1(x) | y = f 2(x) | y = f 3(x) |
| 16. | 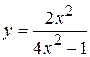
| 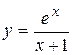
| 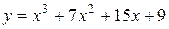
|
| 17. | 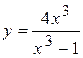
| 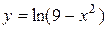
| 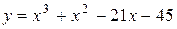
|
| 18. | 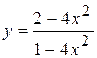
| 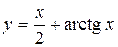
| 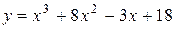
|
| 19. | 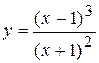
| 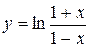
| 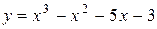
|
| 20. | 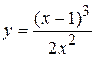
| 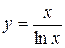
| 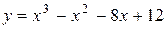
|
| 21. | 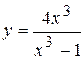
| 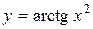
| 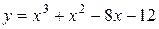
|
| 22. | 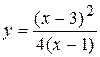
| 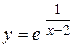
| 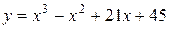
|
| 23. | 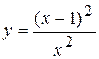
| 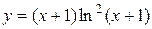
| 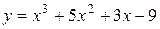
|
| 24. | 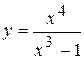
| 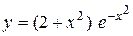
| 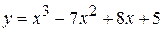
|
| 25. | 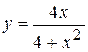
| 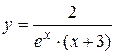
| 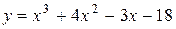
|
| 26. | 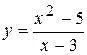
| 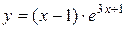
| 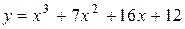
|
| 27. | 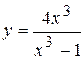
| 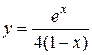
| 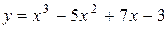
|
| 28. | 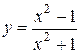
| 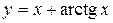
| 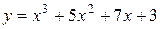
|
| 29. | 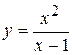
| 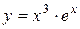
| 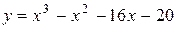
|
| 30. | 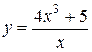
| 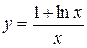
| 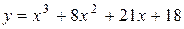
|
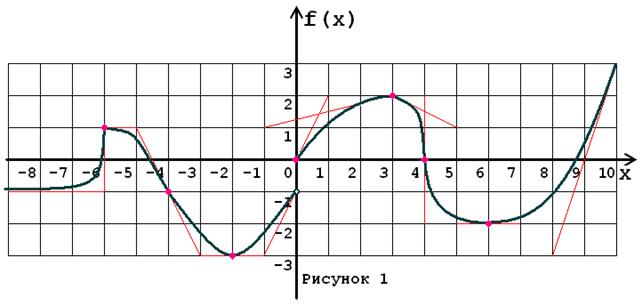
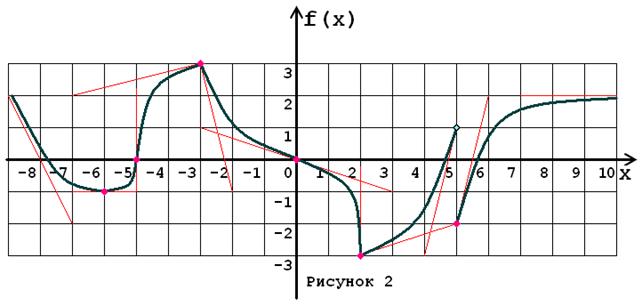
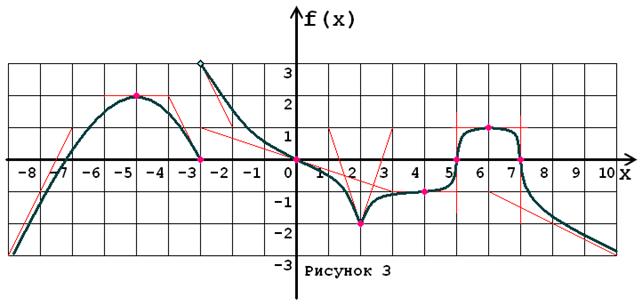
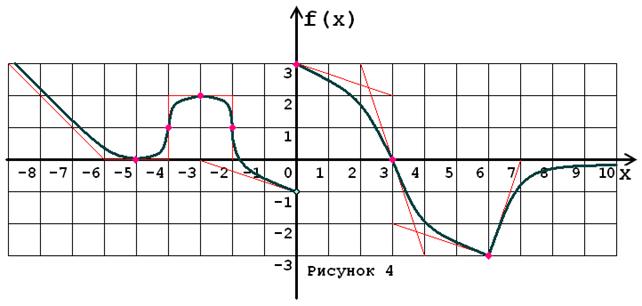
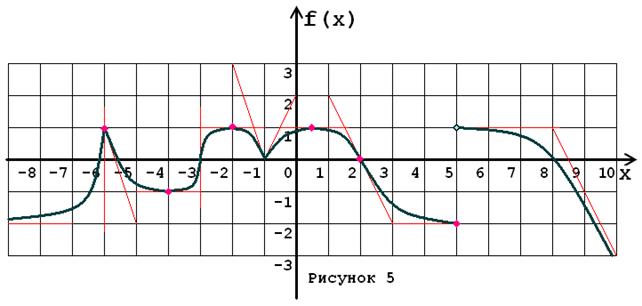
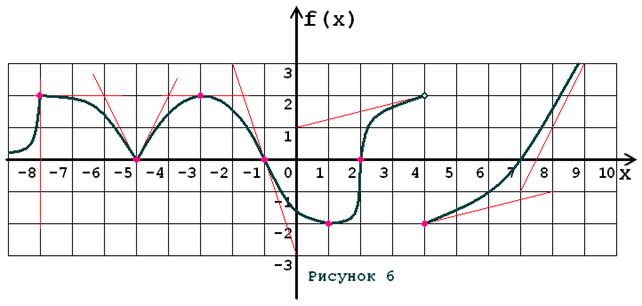
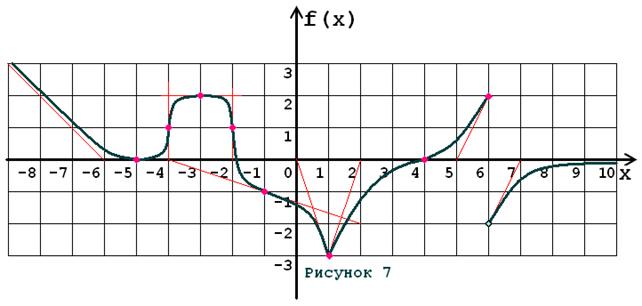
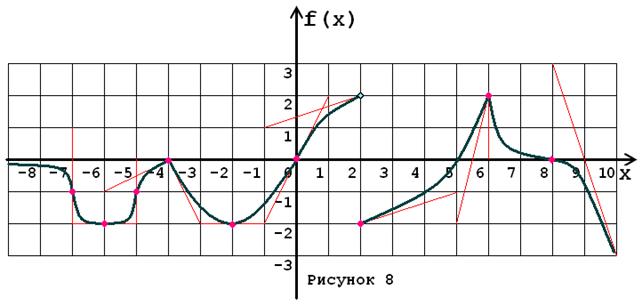
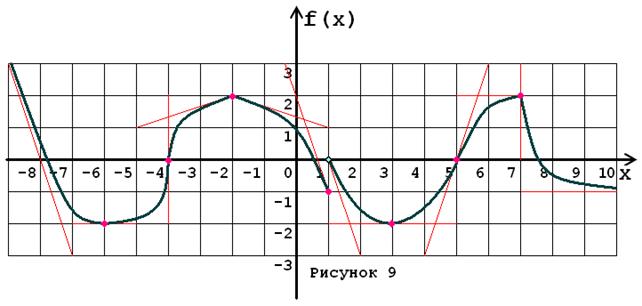
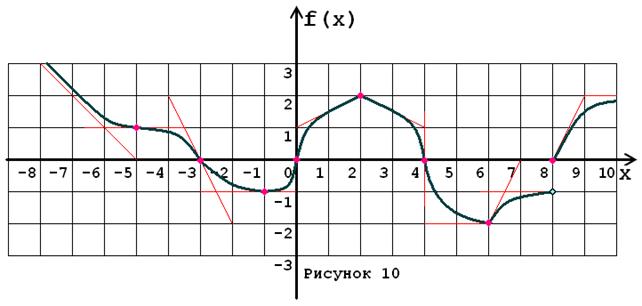
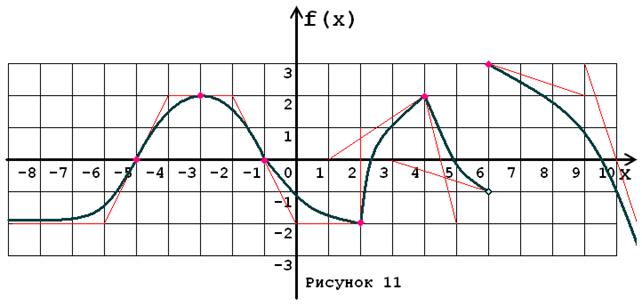
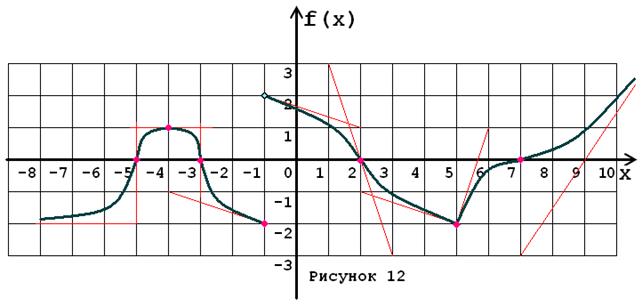
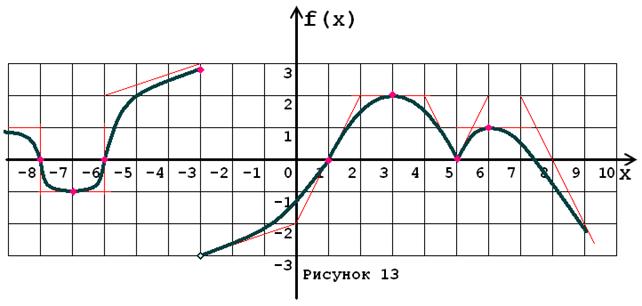
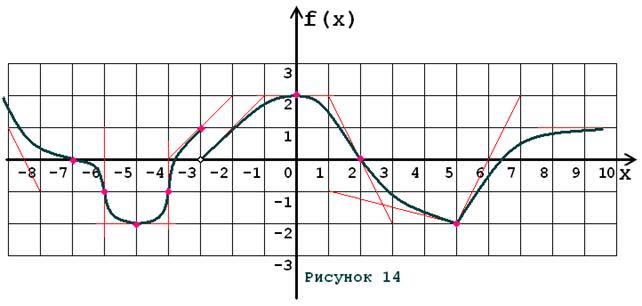
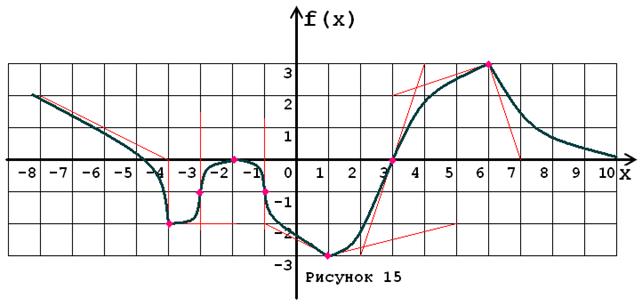
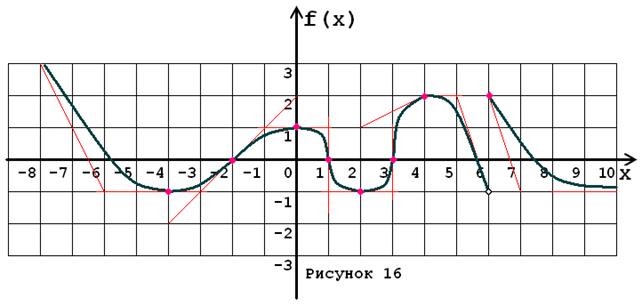
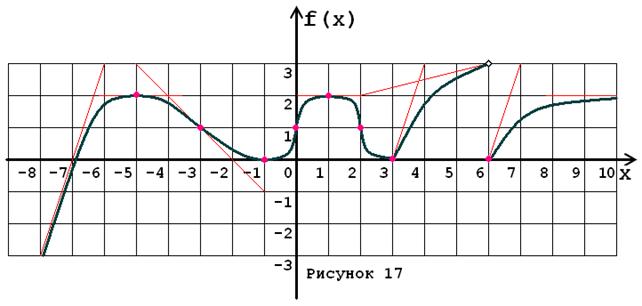
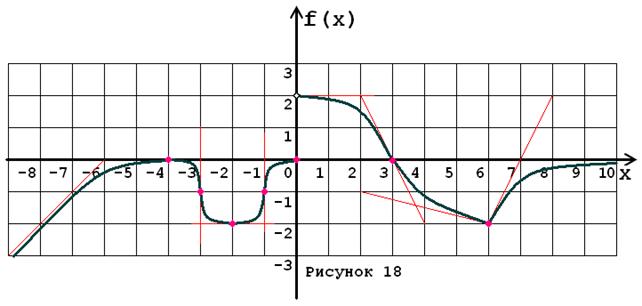
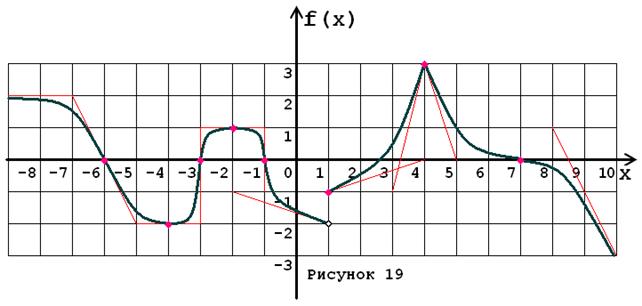
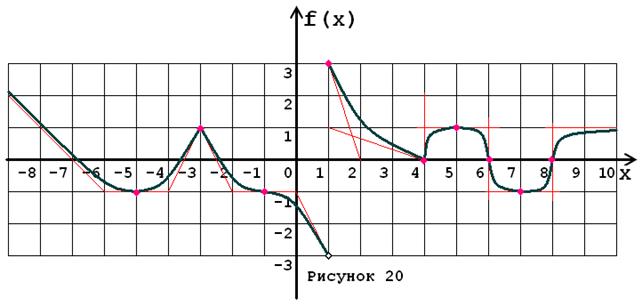
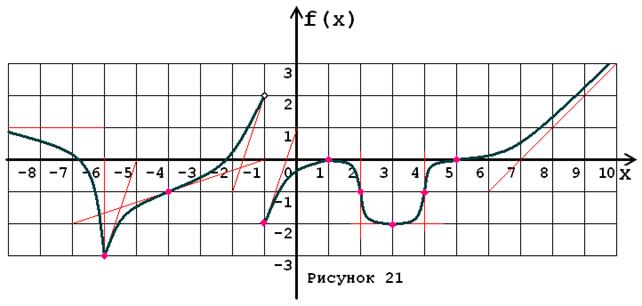
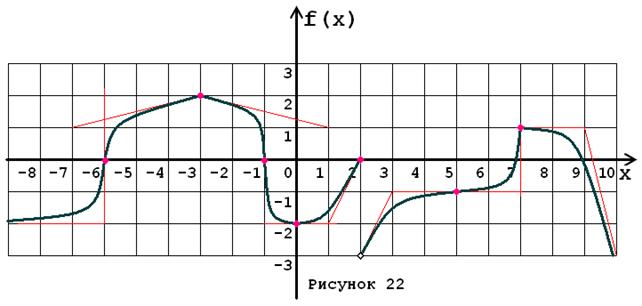
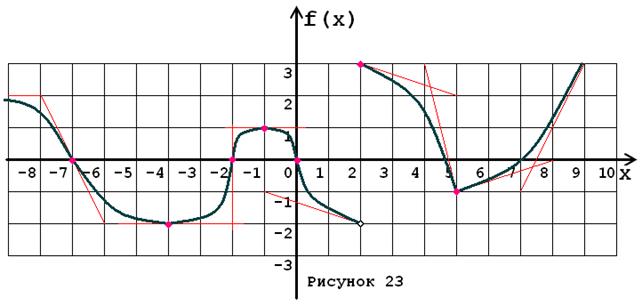
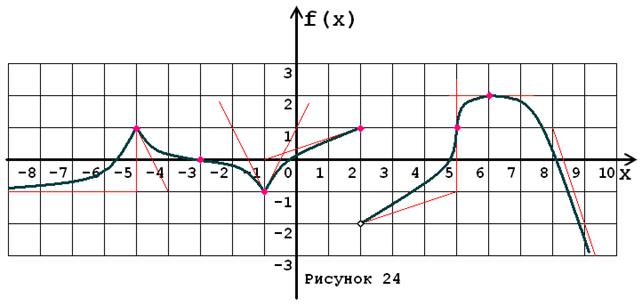
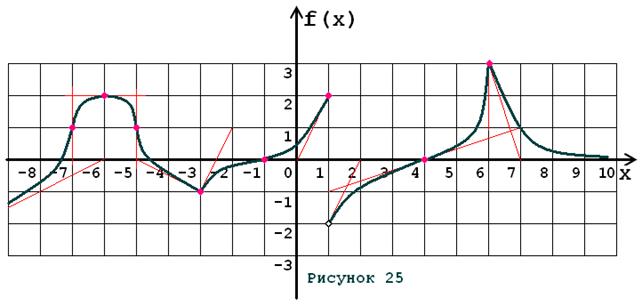
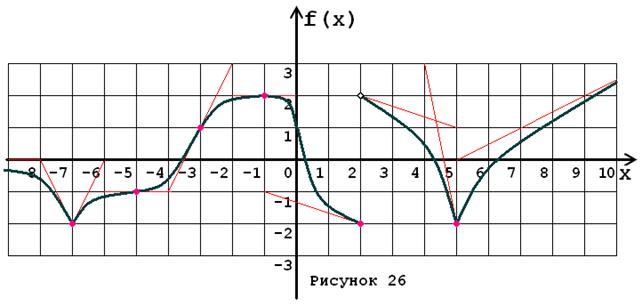
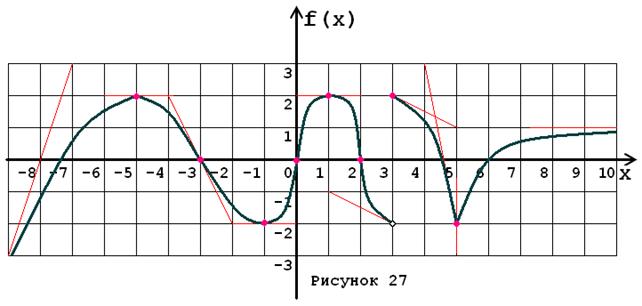
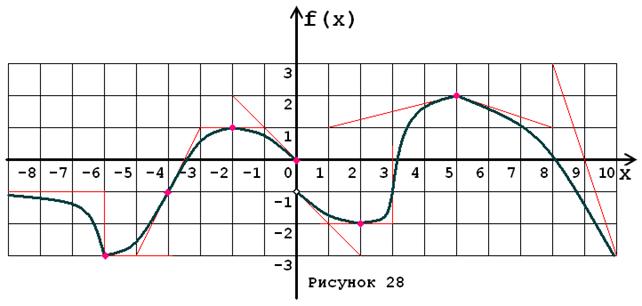
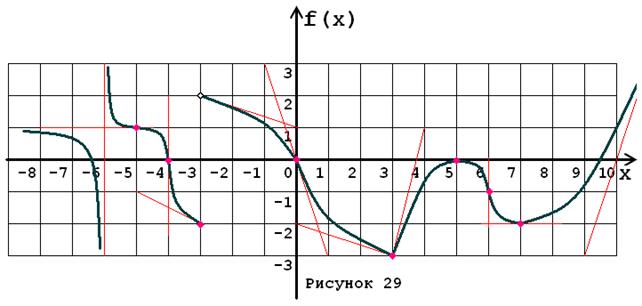
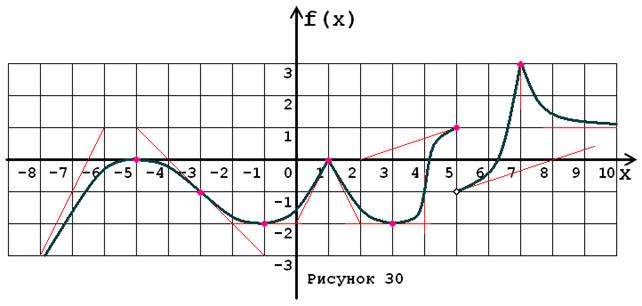
Задача № 5. Опираясь на график функции y = f (x) (рис. 1–30, номер рисунка должен совпадать с номером варианта) для ее производной f¢ (x) найдите:
1. область существования;
2. нули, интервалы знакопостоянства и точки разрывов (установить их характер);
3. вертикальные и горизонтальные асимптоты;
4. интервалы монотонности и экстремумы;
5. построить схематически график f¢ (x), используя результаты проведенного исследования.
 2015-05-13
2015-05-13 664
664







