А) Частоты складываемых колебаний одинаковы

Предположим, что точка одновременно принимает участие в двух гармонических движениях вдоль одного и того же направления, при этом частоты складываемых колебаний равны между собой, отличаются только амплитуды и начальные фазы колебани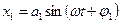й:

и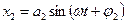

По принципу суперпозиции колебаний полное смещение точки из положения равновесия должно быть равным геометрической сумме смещений, получаемых в каждом из отдельных колебаний. Кроме того, поскольку оба составляющих колебания происходят с одной и той же частотой, то и результирующее колебание будет иметь ту же частоту. Поэтому результат сложения колебаний представим в виде функции:

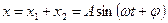
Используя формулы для тригонометрических преобразований, далее запишем, что:

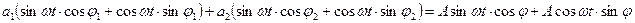
Очевидно, что равенство будет соблюдаться для любого произвольного момента времени, если

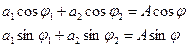
Из последних условий можно определить амплитуду и начальную фазу
результирующего колебания

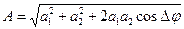(338)

Амплитуда результирующего колебания может принимать различные значения в зависимости от значений амплитуд складываемых колебаний и разности их начальных фаз. Например, если фазы складываемых колебаний отличаются на 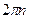, то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний А=а ₁ +а ₂ если же разность фаз равна (2п + 1) , то - разности амплитуд А=а₁-а₂. При разности фаз, равной нечётному числу 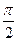амплитуда результирующего колебания равна .

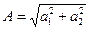Этот же результат можно легко получить, пользуясь векторным представлением колебаний, как это указывалось выше.