Экономико-математическая модель

Задачи с поиском оптимальных решений (задачи оптимизации)

Решения задач оптимизации состоит в поиске оптимального плана с использованием математических моделей и вычислительных методов, которые реализуются с помощью компьютеров и специальных программ-оптимизаторов. Все расчёты сделаны популярной оптимизационною программою Solver (Поиск решений), встроенной в табличную программу MS Excel. Так же здесь рассказано как возможно улучшить полученный результат, что является очень важным для будущего успешного развития предприятия! На сайте доступно показано как можно легко и быстро решать практические задачи производства, используя стандартную программу MS Excel, при минимальных затратах времени и денег, которых всегда не хватает!

Пример 1.

План производства

Постановка задачи. Предприятие имеет запасы 4-х видов ресурсов (мука, жиры, сахар, финансы), с которых производится 2 виды продуктов (хлеб и батон). Известны:

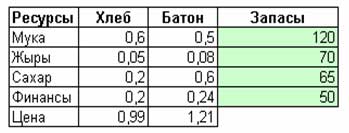
нормы расходов ресурсов на производство единицы продукции;
запасы ресурсов;
цены продуктов;
спрос на хлеб.

Найти оптимальный план производства, при котором доход от реализации произведенной продукции должен быть максимальный.

Экономико-математическая модель.

Найти план (количество хлеба и батонов) такой, чтобы
Доход =0,99*Хлеб+1,21*Батон - мах
При ограничениях:

0,6*Хлеб+0,5*Батон<=120
0,05*Хлеб+0,08*Батон<=70
0,2*Хлеб+0,6*Батон<=65
0,2*Хлеб+0,24*Батон<=50
120<=Хлеб<=150, а также Батон>=0
Реализация в Excel.
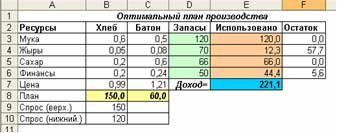
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Доход):

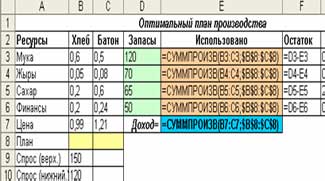
в столбце «Использовано» в каждую ячейку вводим формулу вычисления количества использованных ресурсов: =СУММПРОИЗВ(Норма; План);
в ячейку с Доходом вводим формулу =СУММПРОИЗВ(Цена; План).

Совет. Если таблицу разместить так, как показано, достаточно ввести формулу в первую ячейку, зафиксировать абсолютные координаты плана (нажать F4, чтобы появились символы $) и протянуть это формулу (маркером автозаполнения) к строке Цена.
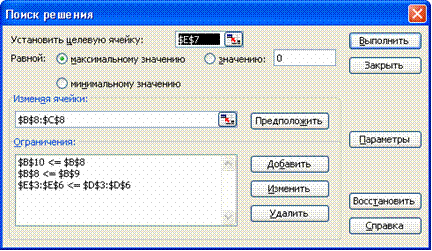
Запускаем программу Поиск решений командой Данные/Анализ / Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.

Результат: чтобы получить максимальный доход в размере 219,1 д. ед. нам нужно производить 150 ед. хлеба и 58,3 ед. батона. С отчета по устойчивости видим, что ресурс Сахар дефицитный и его «Теневая цена» составляет 2 д. ед., это означает то, что если мы увеличим этот ресурс на 1 ед. наш доход увеличится на 2 и будет равен 221,1 д. ед. Интересно то, что «нормированная стоимость» хлеба - позитивное число (0,6) означает, что принудительное увеличение выпуска этого продукта увеличит доход на 0,6 д. ед. за каждую дополнительною единицу, поскольку мы сами занизили эту величину согласно спросу.

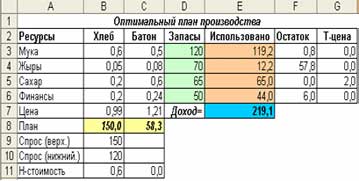
Очевидно, что хлеб и батоны должны быть целыми числами, то после полученного отчета и анализа результата, мы можем, например, увеличить запас Сахара на 1 единицу, снова запустить надстройку Поиск решений и добавить ограничение относительно целочисленных плана. Поскольку при этом ограничение нельзя выводить отчеты, то сначала лучше его не вводить (как мы и сделали), а только после анализа и возможных изменений. Результат при заданных ограничениях: чтобы получить максимальную прибыль в размере 221,1 д. ед. нужно производить 150 ед. хлеба и 60 ед. батонов.