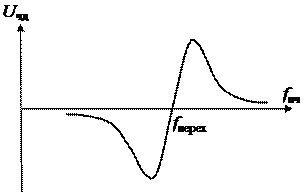Основные сведения. Статическая модель системы

Лабораторная работа № 1

Статическая модель системы

частотной автоподстройки частоты

Основные сведения

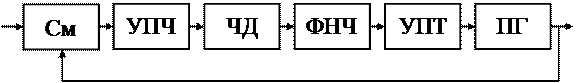Рис. 1

Система частотной автоподстройки частоты (ЧАПЧ) в своем основном применении известна как система автоподстройки частоты гетеродина – АПЧГ (см. рис.1).

Рис. 2

Она включает в себя смеситель См, усилитель промежуточной частоты УПЧ, частотный дискриминатор ЧД, фильтр нижних частот ФНЧ, усилитель постоянного тока УПТ и перестраиваемый гетеродин ПГ. Система АПЧГ используется в супергетеродинных приемниках и обеспечивает близость промежуточной частоты к средней частоте амплитудно-частотной характеристики УПЧ. Сигнал промежуточной частоты формируется на выходе смесителя, на входы которого поступают принимаемый сигнал с частотой f _с и гармоническое колебание с перестраиваемого генератора с частотой f _пг. Промежуточная частота равна разности этих частот: f _пч = f _с – f _пг. Измерение промежуточной частоты производится частотным дискриминатором, зависимость выходного напряжения которого от частоты – дискриминационная характеристика – представлена на рис. 2. Требуемое значение промежуточной частоты задается перехóдной частотой f _перех дискриминационной характеристики.

Поясним коротко работу системы АПЧГ. Если промежуточная частота равна переходной, то напряжение на выходе частотного дискриминатора равно нулю и частота гетеродина не изменяется. При отклонении промежуточной частоты от переходной появляется напряжение на выходе ЧД, которое после фильтрации (ФНЧ) и усиления (УПТ) подается на перестраиваемый гетеродин и вызывает такое изменение его частоты, которое приводит к уменьшению этого отклонения.

Для определения характеристик системы в установившемся режиме составляется статическая модель. В ней отражаются только функциональные преобразования процессов. Опишем эти функциональные преобразования.

Смеситель и УПЧ: f _пч = f _вх – f _пг.

Частотный дискриминатор: U _чд = U _чд(D f), где D f = f _пч – f _перех.

Фильтр нижних частот и усилитель постоянного тока: U _у = K _упт U _чд.

Перестраиваемый гетеродин: f _пг = f _пг0 + D f _пг(U _у), где f _пг0 – частота ПГ при U _у = 0.

Модель, составленная по этим выражениям, показана на рис. 3.

Заменим вычитающие и суммирующее устройства одним вычитающим: D f = f _пч – f _перех = f _вх – f _пг – f _перех = f _вх – f _пг0 – Δ f _пг – f _перех = Δ f _нач – Δ f _пг. Здесь Δ f _нач = f _вх – f _пг0 – f _перех = f _пч0 – f _перех – начальная расстройка. Кроме этого, заменим нелинейную зависимость D f _пг = D f _пг(U _у) линейной D f _пг = K _пг U _у, где K _пг – коэффициент передачи перестраиваемого генератора.

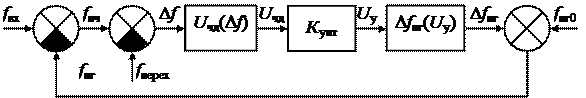Рис. 3

Преобразованная статическая модель показана на рис.4.

K упт K пг U чд(D f) D f пг U чд D f D f нач

Рис. 4

Эта модель описывается системой алгебраических уравнений:

U _чд = U _чд(D f), (1, а)

D f = D f _нач – K _упт K _пг U _чд. (1, б)

Графическое решение этой системы уравнений показано на рис. 5,а. Уравнение (1,а) описывает дискриминационную характеристику частотного дискриминатора. Уравнение (1, б) представляется семейством прямых линий, зависящих от значения начальной расстройки. Эти прямые пересекают горизонтальную ось при D f = D f _нач (уравнение (1,б) при U _чд = 0), а вертикальную – при U _чд = D f _нач/ K, где K = K _упт K _пг (уравнение (1,б) при D f = 0). Значение расстройки в установившемся режиме D f _уст равно горизонтальной координате точки пересечения линий, а значение управляющего напряжения в установившемся режиме U _{у уст} – вертикальной координате этой точки.

На рис. 5,б показана зависимость расстройки в установившемся режиме D f_уст от начальной расстройки. Для линии, отмеченной звездочкой *, показано, как определяется положение точки на зависимости D f_уст (D f_нач).Если увеличивать начальную расстройку от нуля, то будет увеличиваться и расстройка в установившемся режиме. Решение системы уравнений будет перемещаться по линии ОА. Это решение соответствует режиму эффективной автоподстройки, для которого D f_уст <<D f_нач. Начальная расстройка, при которой линия 1, б будет касательной линии 1, а в точке А, определяет границу режима эффективной автоподстройки. При дальнейшем увеличении начальной расстройки решение перей-

Рис. 5

дет в точку В. Расстройка в установившемся режиме будет близка к начальной расстройке. Это режим отсутствия автоподстройки. Начальная расстройка, при которой система АПЧГ выйдет из режима эффективной автоподстройки, называется полосой удержания Df_у. Если продолжать увеличивать начальную расстройку, то расстройка в установившемся режиме будет приближаться к начальной расстройке. Если уменьшать начальную расстройку, то режим отсутствия автоподстройки будет сохраняться до тех пор, пока линия 1, б не станет касательной к линии 1, а в точке С. При дальнейшем уменьшении начальной расстройки система АПЧГ перейдет в режим эффективной автоподстройки (точка D). Начальная расстройка, при которой система АПЧГ входит в режим эффективной автоподстройки, называется полосой захвата Df_з. Режим, соответствующий решению системы алгебраических уравнений на участке АС, будет неустойчив.

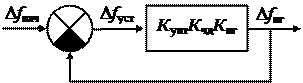Рис. 6

Для оценки качества работы в режиме малых расстроек используется коэффициент автоподстройки К _ап = D f _нач/D f _уст, который показывает, во сколько раз система АПЧГ уменьшает начальную расстройку. Его можно найти из статической модели, если заменить нелинейные зависимости линейными, т.е. U _чд(D f) = К _чдD f и D f _пг(U _у) = К _пг U _у. Тогда нелинейная статическая модель преобразуется в линейную, показанную на рис. 6. Для нее D f _уст = D f _нач – К _упт К _чд К _пгD f _уст. Отсюда К _ап = 1+ К _упт К _чд К _пг.

Компьютерная модель системы показана на рис. 7

A B

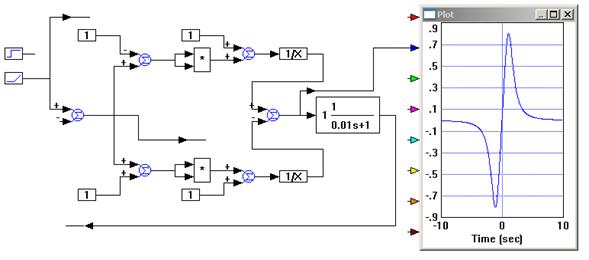Рис. 7

Она состоит из сравнивающего устройства, модели частотного дискриминатора (между точками А и B) и линейного блока, моделирующего УПТ и перестраиваемый гетеродин. На суммирующий вход сравнивающего устройства подается входное воздействие – начальная расстройка D f _нач, с выхода снимается текущая расстройка D f. Модель частотного дискриминатора составлена по дискриминационной характеристике:

U _чд(Δ f) = 1 / [1 + (Δ f – Δ f ₀)²] – 1 / [1 + (Δ f + Δ f ₀)²]. (2)

Операция возведения в квадрат реализуется блоком умножения. В линейный блок помимо безынерционного звена с коэффициентом передачи K = K _упт K _пг введено инерционное звено с передаточной функцией 1/(1 + 0.01 p). Это связано с тем, что цифровую модель системы с обратной связью, состоящую только из безынерционных звеньев, реализовать нельзя.

Дополнительная информация по тематике лабораторной работы изложена в [1, §1.2], [2, §2.1, §7.1].

Задание на предварительный расчет

Решить графически систему алгебраических уравнений (1), учитывая, что дискриминационная характеристика описывается уравнением (2). Исходные данные взять из таблицы:

Вариант
D f 0	0,8	0.9	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9
K

Прямую (1,б): D f = D f _нач – KU _чд удобно построить сначала для D f _нач = K, а затем переносить ее параллельно самой себе для любой другой начальной расстройки. Построить зависимость D f _уст(D f _нач).Определить полосу захвата и полосу удержания.

По дискриминационной характеристике определить K _чд, как тангенс угла наклона касательной в точке Δ f = 0. Найти K _ап = K _чд K.

Программа работы

Из папки “Радиоавтоматика” вызвать лабораторную работу № 1 (Lab_rab1) (П1).

1. Исследование статических характеристик.

1.1. Установить заданные значения параметров K и D f (П5). Отсоединить обратную связь (П2). Подать на вход модели линейно возрастающее воздействие. Подсоединить к Plot выход модели частотного дискриминатора. Установить параметры времени моделирования: начало -10 с, конец 10 с, шаг 0,001 с. (П6). Запустить моделирование (П8). На экране появится изображение дискриминационной характеристики. Так как скорость входного процесса 1 ед.¤с, то горизонтальная шкала в секундах совпадает со шкалой в герцах. Нанести на Plot сетку (П9). Развернуть Plot на весь экран (П11).Сравнить полученную характеристику с рассчитанной. Восстановить изображение.

1.2. Замкнуть обратную связь. К Plot подсоединить входной процесс (D f _нач), выходной процесс (D f _пг) и ошибку (D f). Увеличить окончание времени моделирования до 30 с. (П.6) Запустить моделирование. Если выходной процесс не умещается на экране Plot или, наоборот, процесс заканчивается задолго до окончания развертки, изменить время моделирования. Развернуть изображение на весь экран. Скопировать и сохранить полученные зависимости для отчета. Объяснить их. Замерить полосу захвата, полосу удержания и коэффициент автоподстройки. Для измерения использовать перекрестие (П20). Восстановить размеры окна.

1.3. Снять зависимость полосы захвата, полосы удержания и коэффициента автоподстройки от коэффициента передачи K, уменьшая его по сравнению с заданным в 2, 4 и 8 раз. Результаты измерений по пунктам 1.2 и 1.3 свести в таблицу и построить зависимости. Объяснить их, используя графическое решение системы уравнений, описывающих статическую модель.

2. Исследование входа системы АПЧГ в режим эффективной автоподстройки.

2.1. Установить значение K равным заданному. Отсоединить от входа модели линейное воздействие и подать на вход скачок. Амплитуду скачка установить такой, чтобы она была меньше полосы захвата примерно в 2 раза. Установить параметры времени моделирования: начало -0 с, конец 1 с, шаг 0,0001 с. Запустить моделирование. Развернуть изображение на весь экран. Сохранить изображение для отчета Замерить установившееся значение процесса. Убедиться, что оно соответствует режиму эффективной автоподстройки. Восстановить изображение.

2.2. Установить амплитуду скачка немного меньше полосы захвата. Запустить моделирование. Сохранить изображение для отчета. Обратить внимание на изменение формы переходного процесса. Объяснить, почему так изменился переходный процесс. Замерить установившееся значение выходного процесса. Убедиться, что оно соответствует режиму эффективной автоподстройки.

2.3. Установить амплитуду скачка в интервале между полосой захвата и полосой удержания. Запустить моделирование. Замерить установившееся значение выходного процесса. Какому режиму работы оно соответствует – эффективной автоподстройке или отсутствию автоподстройки? Объяснить, почему достигается именно этот режим.

Завершить работу (П21).

Контрольные вопросы

1. Какой вид имеет функциональная схема системы АПЧГ?

2. Как составляется статическая модель системы АПЧГ и какой вид она имеет?

3. Какими уравнениями описывается статическая модель?

4. Как проводится графическое решение системы алгебраических уравнений, описывающих статическую модель?

5. Как строится зависимость расстройки в установившемся режиме от начальной расстройки?

6. Какой вид имеет статическая характеристика D f _уст(D f _нач) системы АПЧГ?

7. Почему некоторым решениям системы уравнений не может соответствовать установившийся режим в системе АПЧГ?

8. Как определяется коэффициент автоподстройки и от чего он зависит?

9. Как определяются полосы захвата и удержания и от чего они зависят?

Лабораторная работа № 2

Устойчивость линейной системы авторегулирования

Общие сведения

Устойчивость системы означает, что она принципиально может выполнять свои функции. Для линейных систем можно пользоваться следующим определением устойчивости: линейная система устойчива, если при ограниченном входном воздействии выходной процесс тоже ограничен.

Прямым методом анализа устойчивости является решение дифференциального уравнения, описывающего систему:

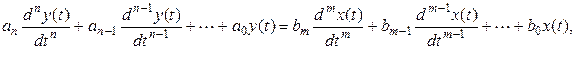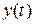где и 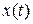- соответственно выходной и входной процессы в системе.

Устойчивость линейной системы не зависит от вида входного воздействия, и можно взять его любым, в том числе и нулевым, но удобнее принять x (t) = 1(t). В этом случае решением дифференциального уравнения является переходная характеристика. И по виду ее можно определить устойчивость системы. Если переходная характеристика стремится к постоянному значению, то система устойчива. Если же переходная характеристика уходит в бесконечность, то неустойчива. Из решения дифференциального уравнения следует, что выходной процесс ограничен, если корни характеристического уравнения

a_npⁿ + a_{n- 1} p^{n- 1} +…+ a ₀ = 0

располагаются в левой полуплоскости.

При анализе устойчивости систем авторегулирования часто используется критерий устойчивости Найквиста. Согласно этому критерию замкнутая система устойчива при устойчивой разомкнутой, если годограф частотной характеристики разомкнутой системы не охватывает точки с координатами (-1, 0).Типовой вид годографа частотной характеристики разомкнутой системы, описываемой передаточной функцией

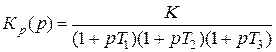, (3)

показан на рис.8.

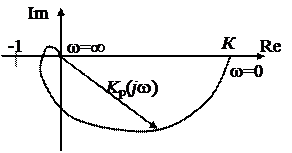Рис. 8

Годограф построен для положительных частот. Он начинается на действительной оси, так как на нулевой частоте коэффициент передачи разомкнутой системы является действительной величиной К _р(0) = К. С ростом частоты модуль коэффициента передачи К _р(w) уменьшается и вносится отрицательный фазовый сдвиг j_р(w), поэтому вектор К _р(j w) поворачивается по часовой стрелке. При w = ¥ К _р(w) = 0 и j_р(w) = - 3p¤2. Для устойчивой системы точка (-1, 0) должна лежать вне фигуры, образованной годографом частотной характеристики и действительной положительной полуосью.

Если в разомкнутую систему входят интеграторы, то годограф частотной характеристики разомкнутой системы начинается в бесконечности. Такие системы называются астатическими. Количество интеграторов равно порядку астатизма. Для системы с одним интегратором, имеющей передаточную функцию

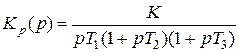, (4)

годограф начинается в третьем квадранте (сплошная линия на рис. 9), а для системы с двумя интеграторами с передаточной функцией

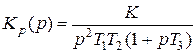– (5)

во втором квадранте (рис. 10), т.к. уже на нулевой частоте интегратор вносит фазовый сдвиг, равный p¤2.

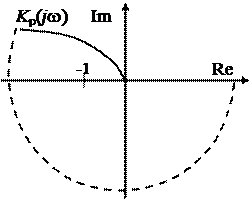Рис.9	Рис. 10

Для построения замкнутого контура в этих случаях требуется к годографу добавить столько четвертей окружности бесконечного радиуса, сколько интеграторов в разомкнутой системе. На рис. 9 и рис. 10 это добавление условно показано пунктирной линией. Замкнутая система с годографом К _р(j w), изображенном на рис. 9, устойчива, а на рис. 10 – неустойчива. Причем последняя является структурно-неустойчивой, т.е. неустойчивой при любом коэффициенте передачи разомкнутой системы.

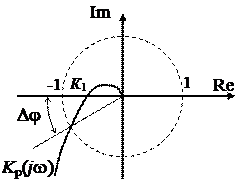Рис. 11

По годографу частотной характеристики разомкнутой системы можно оценить степень устойчивости. Для этого вводится понятие запасов устойчивости по усилению и по фазе. Запас устойчивости по усилению D К показывает, во сколько раз нужно изменить коэффициент передачи разомкнутой системы, чтобы замкнутая из устойчивой стала неустойчивой. Запас устойчивости по фазе Dj показывает, какой фазовый сдвиг нужно ввести в разомкнутую систему, чтобы замкнутая из устойчивой стала неустойчивой. На рис. 11 показано, как эти запасы определяются по годографу частотной характеристики разомкнутой системы. Запас устойчивости по усилению D К =1/| К ₁|, где К ₁ – коэффициент передачи разомкнутой системы на частоте, для которой j_р(w) = -p.Запас устойчивости по фазе равен углу Dj между отрицательной действительной полуосью и линией, соединяющей начало координат с точкой пересечения годографа с окружностью единичного радиуса.

Рис. 12

На практике удобнее пользоваться не годографом частотной характеристики, а амплитудно-частотной и фазочастотной характеристиками. И еще более удобно использовать логарифмические АЧХ (ЛАЧХ или ЛАХ) и ФЧХ (ЛФЧХ или ЛФХ). Критерий Найквиста в этом случае формулируется так: замкнутая линейная система устойчива при устойчивой разомкнутой, если в области частот, где ЛАХ разомкнутой системы положительна, ЛФХ разомкнутой системы или не пересекает значения -p, или пересекает его сверху вниз и снизу вверх одинаковое количество раз. При монотонной ЛФХ разомкнутой системы устойчивость можно определить, сравнивая две характерные частоты: частоту среза w_ср, на которой ЛАХ пересекает ось частот, и критическую частоту w_кр, на которой ЛФХ пересекает значение -p (рис. 12). Для устойчивой системы w_кр>w_ср.

Запас устойчивости по усилению D L определяется на критической частоте как интервал от ЛАХ до оси частот, а запас устойчивости по фазе – на частоте среза как интервал от -p до ЛФХ (рис.12).

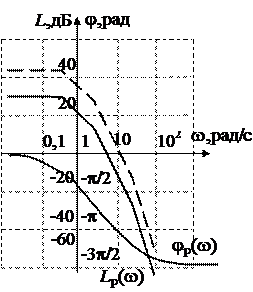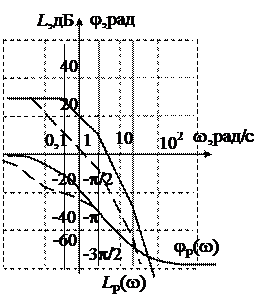Рис. 13	Рис. 14

Логарифмические частотные характеристики позволяют легко и наглядно исследовать влияние параметров системы на ее устойчивость. Рассмотрим это на примере системы с передаточной функцией (3).

На рис. 13 сплошной линией изображены ЛАХ и ЛФХ разомкнутой системы для варианта 13 (таблица на стр. 13).

Замкнутая система устойчива и запас устойчивости по фазе около 25^о. Увеличим коэффициент передачи разомкнутой системы в 5 раз. Тогда ЛАХ поднимется на 20 lg5 = 14 дБ (пунктирная линия). ЛФХ не изменится, так как сопрягающие частоты остались прежними. Частота среза увеличилась и стала больше критической частоты, значит, замкнутая система стала неустойчивой.

На рис.14 показано влияние постоянной времени T ₁ на устойчивость замкнутой системы. При увеличении постоянной времени Т ₁ в 10 раз ЛАХ и ЛФХ сместились в область нижних частот (пунктирные линии). Запас устойчивости по фазе увеличился примерно до 70^о.

Исследование устойчивости для удобства сравнения проводится на трех моделях (рис. 15).

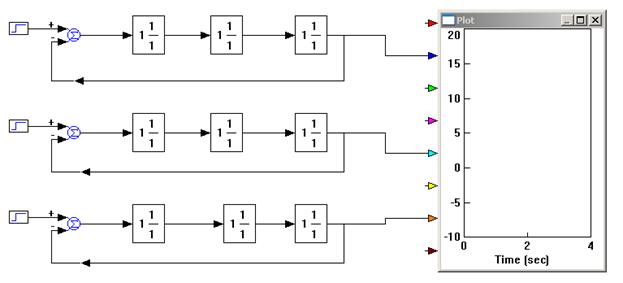Рис. 15

На первой модели реализуется статическая система по передаточной функции (3), на второй модели – астатическая система первого порядка по передаточной функции (4) и на третьей модели – астатическая система второго порядка по передаточной функции (5).Для этого каждая передаточная функция представляется в виде произведения трех сомножителей, и каждый из сомножителей реализуется в отдельном блоке. Например,

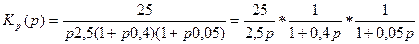
реализуется следующей моделью (рис. 16):

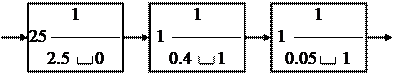Рис. 16

Дополнительная информация по тематике лабораторной работы изложена в [1,§ 5.1, 5.3, 5.4, 5.5], [3,§2.1].

Задание на предварительный расчет

1. Построить на одном графике ЛАХ и ЛФХ разомкнутой системы с передаточными функциями (3) – (5) для значений параметров, заданных таблицей:

Вар.
Т 1,с	0,5	2,5		1,2	1,5							2,5
Т 2,с	0,1	0,5	0,4	0,3	0,2	0,6	0,5	0,4	0,3	0,6	0,2	0,4
10 Т 3,с	0,2	0,4	0,3	0,6	0,5	0,4	0,6	0,4	0,8	0,5	0,2	0,5
К

Методика построения логарифмических частотных характеристик изложена в Приложении 2.

2. Определить запасы устойчивости по усилению и по фазе для устойчивых систем.

3. Составить модели систем с передаточными функциями (3) – (5) с заданными параметрами.

Программа работы

Из папки “Радиоавтоматика” вызвать лабораторную работу № 2 (Lab_rab2) (П1). На рабочем столе Windows появятся три модели. Установить заданные значения постоянных времени и коэффициента передачи (П5).

1. Исследование частотных характеристик разомкнутой системы и устойчивости замкнутой системы.

1.1. В первой модели выделить разомкнутую систему, которая включает все блоки за исключением вычитающего устройства (П4), и просмотреть годограф частотной характеристики (П14). В пакете VisSim годограф строится для положительных и отрицательных частот, поэтому он симметричен относительно действительной оси. Нанести сетку (П9). Развернуть годограф на весь экран (П11). Сохранить годограф для отчета. Сделать вывод об устойчивости замкнутой системы. Замерить запас устойчивости по усилению. Для этого рассмотреть более подробно годограф в окрестности точки (-1, 0), изменив границы изображения и приняв их равными –2 и 2 по обеим координатным осям (П13). Восстановить размер изображения. Т

То же самое проделать для второй и третьей моделей. Закрыть все окна с годографами.

1.2. В первой модели выделить разомкнутую систему и просмотреть ЛАХ и ЛФХ (П16). Установить шкалу по оси Y в децибелах (П15), если эта ось проградуирована в других единицах. Нанести на ЛАХ и ЛФХ сетку. При необходимости скорректировать диапазон частот, в котором просматриваются характеристики (П7) Сравнить эти характеристики с построенными при подготовке к работе. При желании сохранить ЛАХ и ЛФХ для отчета. Замерить частоту среза, запас устойчивости по фазе, критическую частоту и запас устойчивости по усилению. Сравнить их с рассчитанными при подготовке к работе. Закрыть окна с частотными характеристиками.

1.3. Проделать п.1.2 для второй и третьей моделей.

2 Исследование устойчивости по переходным процессам.

2.1. Подать на входы всех трех моделей единичный скачок. Выходы всех моделей подсоединить к Plot. Установить шаг моделирования равным 0,001 с (П.6). Запустить моделирование. Если выходной процесс в неустойчивой системе принимает очень большие значения и нельзя просмотреть переходные характеристики, уменьшить время моделирования (П6) или ограничить диапазон просматриваемых значений по вертикальной оси (П. 13). Сохранить переходные характеристики для отчета. Сделать вывод об устойчивости систем.

2.2. Исследование влияния коэффициента передачи разомкнутой системы на устойчивость замкнутой системы.

На всех трех моделях реализовать статическую систему с передаточной функцией (3).Постоянные времени установить в соответствии с заданием, а коэффициент передачи К установить различным: для первой модели – равным заданному, а для двух других – в два раза больше и в два раза меньше заданного.

Просмотреть переходные характеристики. Сохранить их для отчета. Объяснить различие между ними, используя ЛАХ и ЛФХ разомкнутой системы.

2.3. Исследование влияния постоянной времени Т ₁ инерционного звена на устойчивость замкнутой системы.

На всех трех моделях установить коэффициент передачи К равным заданному, а постоянную времени Т ₁ различной: для одной модели – равной заданной, а для двух других – больше и меньше заданной в 10 раз. Просмотреть переходные характеристики замкнутой системы. Сохранить их для отчета. Объяснить различие между ними, используя ЛАХ и ЛФХ разомкнутой системы..

Завершить работу (П21).

Контрольные вопросы

1. Какое требование предъявляется к выходному процессу устойчивой линейной системы?

2. Как определяется устойчивость системы по виду переходной характеристики?

3. Как формулируется критерий устойчивости Найквиста?

4. Какой вид имеют годографы частотной характеристики для систем без интеграторов и с интеграторами?

5. Как определяется устойчивость замкнутой системы по ЛАХ и ЛФХ разомкнутой системы?

6. Как определяются запасы устойчивости по годографу частотной характеристики разомкнутой системы?

7. Как определяются запасы устойчивости по ЛАХ и ЛФХ разомкнутой системы?

8. Как влияет коэффициент передачи разомкнутой системы на устойчивость замкнутой системы?

9. Как влияет постоянная времени инерционного звена на устойчивость замкнутой системы?

Лабораторная работа № 3

Частотные и переходные характеристики

систем авторегулирования

Основные сведения

Частотная и переходная характеристики замкнутой системы являются показателями качества при гармоническом и скачкообразном воздействиях. Если задающее воздействие гармоническое:

x _з(t) = A cosw t,

то выходной процесс линейной системы тоже гармонический:

y (t) = AK _з(w)cos(w t + j_з(w)),

где К_з (w) и j_з(w), соответственно, АЧХ и ФЧХ замкнутой системы.

Ошибка

d(t) = x_з (t) – y (t) = A cosw t – AK _з(w)cos(w t + j_з(w))

будет равна нулю только при К_з (w) = 1 и j_з(w) = 0. Это требование к идеальной частотной характеристике замкнутой системы. Если все составляющие спектра задающего воздействия попадают в область частот,

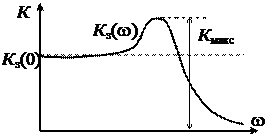Рис. 17

где частотная характеристика идеальна, то воздействие отрабатывается без ошибки. В противном случае возникает динамическая ошибка. Для оценки качества регулирования по АЧХ замкнутой системы используется показатель колебательности М = К _макс/ К _з(0) (см. рис. 17). Обычно величина показателя колебательности меньше 2.

По форме АЧХ можно судить о переходной характеристике системы. Так, если АЧХ будет монотонной, то и переходная характеристика монотонная, если в АЧХ будет подъем в области верхних частот, то переходная характеристика колебательная.

Рис. 18

Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 18). Обычно используются следующие числовые параметры переходной характеристики:

время достижения первого максимума t_m,

время регулирования t _рег,

период колебаний на вершине Т _в,

перерегулирование Δ h_m / h _уст ≈ Δ h_m = (h _макс – h _уст).

Так как частотная характеристика замкнутой системы однозначно связана с частотной характеристикой разомкнутой системы, то можно установить связь, по крайней мере, качественную, между логарифмическими частотными характеристиками разомкнутой системы и параметрами переходной характеристики замкнутой системы. Так, чем меньше запас устойчивости по фазе, тем больше перерегулирование и медленнее затухание колебаний на вершине. Существует следующая приближенная связь между запасом устойчивости по фазе и перерегулированием:

Δ h_m (в %) = 70 – Δ φ (в град) (6)

при условии, что запас устойчивости по фазе 30⁰ < Dj < 70⁰.

Временные параметры переходной характеристики связаны с частотой среза w_ср. Чем больше частота среза, тем шире полоса пропускания замкнутой системы и меньше все временные параметры.

Как правило, системы, обладающие удовлетворительным качеством регулирования, имеют запас устойчивости по фазе от 30 до 70⁰. Как можно обеспечить такой запас устойчивости по фазе? Если ЛАХ пересекает ось частот под наклоном -20 дБ/дек. и длина участка с таким наклоном достаточно велика, то запас устойчивости по фазе близок к 90⁰. Такую связь можно установить, например, по логарифмическим частотным характеристикам интегрирующего звена (рис. П1)). Во всем диапазоне частот его ЛАХ идет под наклоном –20 дБ/дек., а фазовый сдвиг равен –90⁰. Если же ЛАХ пересекает ось частот под наклоном –40 дБ/дек. и длина участка с таким наклоном достаточно велика, то запас устойчивости по фазе близок к нулю. Поэтому такой наклон ЛАХ при пересечении оси частот нежелателен.

Наиболее легко обеспечиваются приемлемые запасы устойчивости по фазе, если ЛАХ разомкнутой системы пересекает ось частот под наклоном –20 дБ/дек и длина участка с таким наклоном составляет около 1,5 декады. С этим участком сопрягаются участки ЛАХ с наклонами –40 или –60 дБ/дек. Можно выделить 4 типа ЛАХ в окрестности частоты среза, отличающиеся наклонами: 1) -40, -20, -40; 2) -40, -20, -60; 3) -60, -20, -40; 4) -60, -20, -60. Если ЛАХ продлить в области нижних и верхних частот без изменения наклона, то передаточная функция разомкнутой системы для каждого из этих типов ЛАХ запишется, соответственно:

,	,
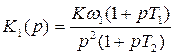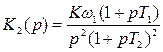		(7)
,	,

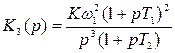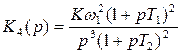где ω₁= 1/ Т ₁,, К = 10 ^{L /20}, L – значение ЛАХ на частоте ω₁.

Запас устойчивости по фазе зависит как от длины участка с наклоном –20 дБ/дек., так и от соотношения сопрягающих частот ω₁ и ω₂ и частоты среза ω_ср, а также от типа ЛАХ. Для соответствующего типа ЛАХ он определяется выражениями:

Δ φ ₁ = arctgω_ср T ₁ – arctgω_ср Т ₂,

Δ φ ₂ = arctgω_ср Т ₁ – 2arctgω_ср Т ₂, (8)

Δ φ ₃ = -90⁰ + 2arctgω_ср Т ₁ – arctgω_ср Т ₂,

Δ φ ₄ = -90⁰ + 2arctgω_ср Т ₁ – 2arctgω_ср Т ₂.

Сравним запасы устойчивости по фазе для первого и четвертого типов ЛАХ при одинаковой длительности участка с наклоном –20 дБ/дек, равном 1,5 декады (см. рис. 19). Приняты значения Т ₁ = 1 с и Т ₂ = 0,03 с. ЛФХ, соответствующая ЛАХ первого типа, получается сложением ЛФХ

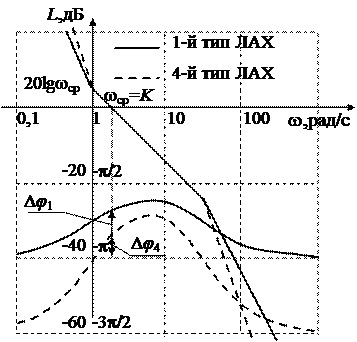Рис. 19

двух интегрирующих звеньев, форсирующего звена с постоянной времени Т ₁ и инерционного звена с постоянной времени Т ₂. ЛФХ, соответствующая ЛАХ четвертого типа, получается сложением ЛФХ трех интегрирующих звеньев, двух форсирующих и двух инерционных звеньев Видим, что с увеличением наклонов участков ЛАХ, сопрягаемых с участком с наклоном –20 дБ/дек, запас устойчивости по фазе становится меньше. Заметим также, что запас устойчивости по фазе уменьшается с приближением w_ср к w₁ или w₂.

Мы рассмотрели связь формы переходной характеристики замкнутой системы с видом ЛАХ и ЛФХ разомкнутой системы в диапазоне средних частот, когда -(20…30) дБ < L _р(w) < <(30…40) дБ. Рассмотрим теперь диапазон нижних и верхних частот.

В диапазоне нижних частот L _р(w) > (30…40) дБ и K _р(w) >> 1.

Так как

,

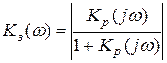то АЧХ замкнутой системы в этом диапазоне частот близка к 1, и переходная характеристика h _з(t) практически не зависит от вида частотной характеристики разомкнутой системы. В диапазоне верхних частот L _р(w) < -(20…30) дБ и K _р(w) << 1. Тогда K _з(w) ≈ K _р(w) << 1 и влияние вида АЧХ разомкнутой системы на переходную характеристику замкнутой системы тоже незначительно. Следовательно, переходная характеристика замкнутой системы в основном определяется среднечастотным участком частотной характеристики разомкнутой системы.

Для удобства сравнения процессов в системах, отличающихся друг

от друга или передаточными функциями, или параметрами, исследование проводится параллельно на трех моделях. Эти модели в изображении VisSim приведены на рис. 20. Каждая содержит три линейных звена, передаточные функции которых определяются разложением передаточной функции разомкнутой системы на три сомножителя. Например, для передаточной функции четвертого типа:

.

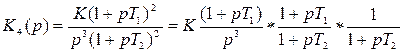Дополнительная информация по тематике лабораторной работы изложена в [1, §6.2, 6.3], [3, §2.2].

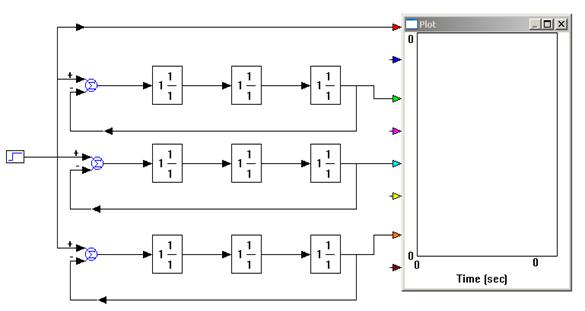Рис. 20

Задание на предварительный расчет

1. Построить ЛАХ и ЛФХ по данным таблицы, приняв Т ₁ = 1 с и Т ₂ = =0,01 с.

Вариант

Тип ЛАХ

wср, рад/с

Построение ЛАХ начать с участка с наклоном -20 дБ/дек, пересекающего ось частот на частоте ω_ср и к нему пристроить участки ЛАХ с наклонами -40 или -60 дБ/дек. Как видно из рис. 19, при ω₁=1 коэффициент передачи K = ω_ср. Записать выражение для передаточной функции разомкнутой системы с числовыми значениями всех параметров, и представить ее в виде произведения трех сомножителей, удобном для моделирования.

2. Записать передаточные функции разомкнутой системы с измененными постоянными времени в соответствии с п. 1.1 Программы работы. Рассчитать запас устойчивости по фазе для всех вариантов по соответствующему выражению (8).

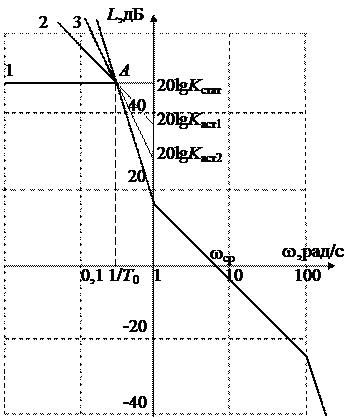Рис. 21

3. Построить ЛАХ разомкнутой системы с заданной ЛАХ в области средних частот для систем: статической и астатических первого и второго порядка. Коэффициент передачи для статической системы K = K _ст принять равным 25 и 100. Коэффициенты передачи астатических систем и постоянную времени низкочастотного инерционного звена T ₀ определить по построенным ЛАХ. Построение ЛАХ и определение параметров показано на рис. 21 на примере ЛАХ четвертого типа. Сначала проводится прямая, параллельная оси частот, через точку (1, 20lg K _стат). По ней проводится ЛАХ для статической системы (1). По точке пересечения А определяется постоянная времени T ₀. Через эту точку проводятся низкочастотные асимптоты ЛАХ астатической системы 1-го порядка (2) с наклоном -20 дБ/дек и 2-го порядка (3) с наклоном -40 дБ/дек. Выражения для передаточных функций составляются по построенным ЛАХ:

1) для статической системы ,

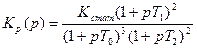2) для астатической системы 1-го порядка ,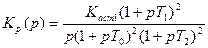

3) для астатической системы 2-го порядка .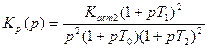

4. Составить модели исследуемых систем с заданными и рассчитанными параметрами, удобные для компьютерного моделирования в среде VisSim.

Программа работы

Из папки “Радиоавтоматика” вызвать лабораторную работу № 3 (Lab_rab3) (П1). Появятся три модели одинаковой структуры.

1. Исследование влияния вида ЛАХ разомкнутой системы в окрестности частоты среза на частотные и переходные характеристики замкнутой системы.

1.1. Составить все три модели по передаточной функции (7), соответствущей заданному типу ЛАХ. Все параметры первой модели установить равными заданным и рассчитанным. Вторая модель отличается от первой постоянной времени Т ₁. Ее надо установить в 2 раза меньше заданной, если длина участка от w₁ до w_ср меньше декады, или в 5 раз меньше заданной, если длина этого участка больше или равна одной декаде. Вместе с изменением Т ₁ необходимо изменить и коэффициент передачи, так как он зависит от w₁. Во сколько раз уменьшится Т ₁, во столько же раз увеличится w₁. Третья модель отличается от второй постоянной времени Т ₂. Ее надо взять в 2 раза больше заданной, если длина участка от w_ср до w₂ меньше или равна одной декаде, и в 5 раз больше заданной, если эта длина больше одной декады.

1.2. В первой модели выделить разомкнутую систему (П 4). Просмотреть ЛАХ и ЛФХ (П 16).Скорректировать, если нужно, диапазон частотного анализа (П 7) Нанести сетку на ЛАХ и ЛФХ (П 9). Замерить частоту среза и запас устойчивости по фазе. Выделить замкнутую систему. Просмотреть АЧХ замкнутой системы. Перейти от логарифмической шкалы по вертикальной оси к линейной (П 17). Развернуть изображение на весь экран. Замерить коэффициент передачи замкнутой системы на частоте среза. Если АЧХ имеет подъем в области верхних частот, замерить частоту, на которой усиление будет максимальным, и значение показателя колебательности. Сохранить АЧХ замкнутой системы для отчета.

1.3. Проделать п.1.2 для второй и третьей моделей.

1.4. Подать на входы всех трех моделей скачок. Выходы всех моделей подсоединить к Plot. Установить временные параметры моделирования (6): Range End – 2 с, Step Size – 0,001 с Запустить моделирование. Если нужно, скорректировать время моделирования. Сохранить переходные характеристики для отчета. Объяснить изменения в них. Для каждой из переходных характеристик замерить время достижения первого максимума, период колебаний на вершине переходной характеристики. Сопоставить эти параметры с частотой среза. Замерить перерегулирование. Сопоставить его с запасом устойчивости по фазе (6).

2. Исследование влияния вида ЛАХ разомкнутой системы в области нижних частот на переходную характеристику замкнутой системы.

2.1. Составить модели систем: статической и астатических 1-го и 2-го порядка по передаточным функциям, полученным в п. 3 предварительного расчета. Установить Т ₁ = 1, Т ₂ = 0.01.

2.2. Установить коэффициенты передачи разомкнутой системы и постоянную времени Т ₀, рассчитанные для K _стат = 100. Просмотреть переходные характеристики. Сохранить их для отчета.

2.3. Проделать п. 2.2. для K _стат = 25. Объяснить различия в переходных характеристиках.

Завершить работу (П21).

Контрольные вопросы

1. Для каких воздействий показателями качества являются частотная и переходная характеристики?

2. Какие требования накладываются на АЧХ и ФЧХ замкнутой системы для безошибочной отработки гармонического воздействия?

3. Какие числовые параметры используются для описания переходной характеристики САР?

4. Как связан вид переходной характеристики с формой АЧХ?

5. Как связаны параметры переходной характеристики замкнутой системы с запасом устойчивости по фазе?

6. При каком виде ЛАХ в окрестности частоты среза наиболее легко обеспечить приемлемые запасы устойчивости по фазе?

7. Как записывается передаточная функция разомкнутой системы К _р(р) в окрестности частоты среза?

8. Как влияет на запас устойчивости по фазе длина участка с наклоном -20 дБ/дек, положение ω_ср на этом участке, наклон ЛАХ на сопрягающих участках?

9. Как влияет на переходную характеристику замкнутой системы вид ЛАХ разомкнутой системы в области нижних частот?

Лабораторная работа № 4

Динамические ошибки в системах авторегулирования