Пусть измеряется величина «а» (время, масса и т.д.).
Обозначим результат i-го измерения через 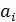 (i=1,2,3…). Теория вероятности доказывает, что ближе всего к истинному значению лежит среднее арифметическое значение результатов измерений:
(i=1,2,3…). Теория вероятности доказывает, что ближе всего к истинному значению лежит среднее арифметическое значение результатов измерений:
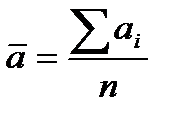
Абсолютная погрешность i-го измерения равна:
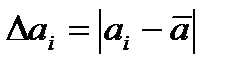
Показателем точности проведенных измерений считается среднеквадратичная погрешность результата n измерений:
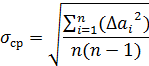
В прямых многократных измерениях результирующая погрешность определяется как погрешностями самой измеряемой величины, так и погрешностью измерительного прибора (инструментальной погрешностью). За инструментальную погрешность 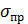 обычно принимается точность прибора. Если точность прибора не указана, то за
обычно принимается точность прибора. Если точность прибора не указана, то за 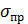 принимается половина цены деления минимальной шкалы измерительного прибора.
принимается половина цены деления минимальной шкалы измерительного прибора.
В проводимых лабораторных работах с надежностью около 70% за доверительный интервал (абсолютную погрешность результатов измерений) принимается величина:
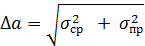
В этом случае результат измерений представляется в виде:
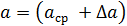
Значения 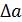 берется с одной значащей цифрой, а величина
берется с одной значащей цифрой, а величина 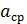 округляется до соответствующего разряда в
округляется до соответствующего разряда в 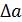 .
.
Относительная погрешность измерений равна:
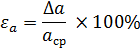
 2015-05-13
2015-05-13 425
425








