Средние величины. Характеризуют значения признака, вокруг которого концентрируются наблюдения.
Основные свойства средней арифметической:
a) средняя арифметическая постоянной равна самой постоянной;
b) если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз;
c) 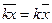 или
или 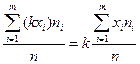 ;
;
d) если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число;
e) 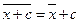 или
или 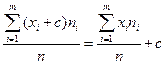 ;
;
f) средняя арифметическая отклонений вариантов от средней арифметической равна нулю: 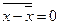 или
или 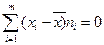 ;
;
g) средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков;
h) 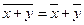 ;
;
i) если ряд состоит из нескольких групп, то общая средняя равна средней арифметической групповых средних, причем весами являются объемы групп: 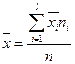 .
.
Структурные или порядковые средние:
Медианой 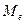 вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.
вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.
Модой 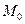 вариационного ряда называется вариант, которому соответствует наибольшая частота.
вариационного ряда называется вариант, которому соответствует наибольшая частота.
1. Вариационный размах 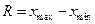 .
.
2. Среднее линейное отклонение – средняя арифметическая абсолютных величин отклонений вариантов от их средней арифметической: 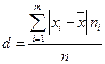 .
.
3. Дисперсия 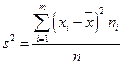 .
.
4. Среднее квадратическое отклонение 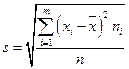 .
.
5. Коэффициент вариации: равен процентному отношению среднего квадратического отклонения к средней арифметической 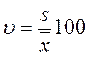 %.
%.
Основные свойства дисперсии, аналогичные свойствам дисперсии случайной величины:
a. Дисперсия постоянной равна нулю.
b. Если все варианты увеличить (уменьшить) в одно и то же число к, то дисперсия увеличится (уменьшится в 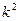 раз):
раз): 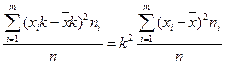 .
.
c. Если все варианты увеличить (уменьшить) на одно и то же число, то дисперсия не измениться.
d. Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической: 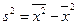 .
.
e. Если ряд состоит из нескольких групп наблюдений, то общая дисперсия равна сумме средней арифметической групповых дисперсий и межгрупповой дисперсии: 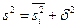 ,
, 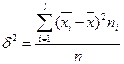 – межгрупповая дисперсия;
– межгрупповая дисперсия; 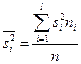 – средняя арифметическая групповых дисперсий.
– средняя арифметическая групповых дисперсий.
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Оценкой 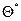 параметра
параметра 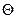 называют всякую функцию результатов наблюдений над случайной величиной Х (иначе статистику), с помощью которой судят о значении параметра
называют всякую функцию результатов наблюдений над случайной величиной Х (иначе статистику), с помощью которой судят о значении параметра 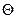 :
: 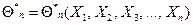 .
.
Оценка в отличие от оцениваемого параметра является случайной величиной.
Например, для оценки математического ожидания нормального распределения служит функция – среднее арифметическое наблюдаемых значений признака.
Несмещенной называют статистическую оценку 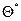 (тета), математическое ожидание которой равно оцениваемому параметру
(тета), математическое ожидание которой равно оцениваемому параметру 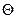 при любом объеме выборки, т. е.
при любом объеме выборки, т. е.
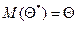 .
.
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Пояснение. Пусть 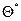 – стат. оценка неизвестного параметра
– стат. оценка неизвестного параметра 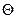 теоретического распределения. Беря разные выборки одного и того же объема получаем оценки
теоретического распределения. Беря разные выборки одного и того же объема получаем оценки 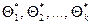 , которые различны между собой.
, которые различны между собой. 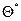 – как случайная величина, а
– как случайная величина, а 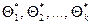 ее значения. Если
ее значения. Если 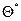 дает приближенное значение с избытком, тогда каждое найденное значение
дает приближенное значение с избытком, тогда каждое найденное значение 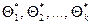 больше истинного значения
больше истинного значения 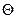 . Тогда и
. Тогда и 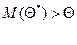 . Если
. Если 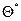 дает оценку с недостатком, то
дает оценку с недостатком, то 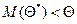 . Таким образом, использование такой оценки привело бы к систематическим (одного знака) ошибкам.
. Таким образом, использование такой оценки привело бы к систематическим (одного знака) ошибкам.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
Состоятельной называют статистическую оценку, которая при 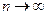 стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.
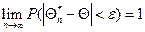 или
или 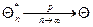 .
.
Примеры оценок: выборочная дисперсия есть смещенная и состоятельная оценка генеральной дисперсии; выборочное среднее является несмещенной и состоятельной оценкой.
Интервальной называют оценку, которая определяется двумя числами – концами интервалов.
Оценка 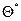 будет тем точнее оценивать параметр
будет тем точнее оценивать параметр 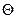 , если
, если 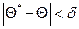 , где
, где 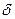 очень маленькое.
очень маленькое.
Значение 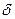 характеризует точность оценки.
характеризует точность оценки.
Надежностью (доверительной вероятностью) оценки называют вероятность 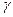 , с которой осуществляется неравенство
, с которой осуществляется неравенство 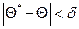 .
.
Наиболее часто задают надежность равную 0,95; 0,99; 0,999.
Вероятность того, что 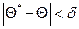 равна
равна 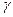 , запишется
, запишется 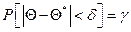 или
или 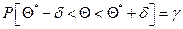 . То есть интервал
. То есть интервал 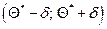 заключает в себе (покрывает) неизвестный параметр
заключает в себе (покрывает) неизвестный параметр 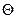 с вероятностью
с вероятностью 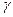 .
.
Доверительным интервалом называют интервал 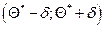 , который покрывает неизвестный параметр с заданной надежностью
, который покрывает неизвестный параметр с заданной надежностью 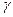 .
.
Доверительный интервал для оценки математического ожидания нормального распределения при известном 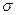 .
.
Будем рассматривать выборочную среднюю 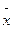 как случайную величину
как случайную величину 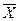 . Математическое ожидание этих величин равно
. Математическое ожидание этих величин равно 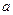 и среднее квадратическое отклонение
и среднее квадратическое отклонение 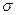 .
.
Если случайная величина Х распределена нормально, то выборочная средняя 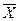 , найденная по независимым наблюдениям также распределена нормально.
, найденная по независимым наблюдениям также распределена нормально.
Пусть выполняется соотношение 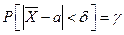 с заданной надежностью
с заданной надежностью 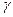 .
.
Используя функцию Лапласа 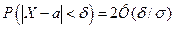 . Сделав соответствующую замену, получим:
. Сделав соответствующую замену, получим:
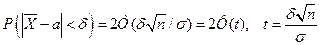 ;
;
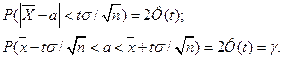
То есть доверительный интервал 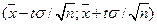 покрывает неизвестный параметр
покрывает неизвестный параметр 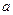 , точность оценки
, точность оценки 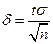 . Число t определяется по таблице функции Лапласа
. Число t определяется по таблице функции Лапласа 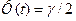 . Таким образом, получаем интервал:
. Таким образом, получаем интервал:
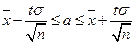 . (4.1)
. (4.1)
Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном 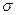 .
.
На практике почти всегда генеральная дисперсия неизвестна.
В этом случае используется следующая формула для построения доверительного интервала:
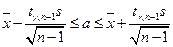 , (4.2)
, (4.2)
где 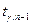 – статистика Стьюдента с уровнем надежности
– статистика Стьюдента с уровнем надежности 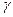 и числом степеней свободы
и числом степеней свободы 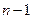 ;
; 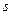 – смещенная оценка среднего квадратического отклонения.
– смещенная оценка среднего квадратического отклонения.
Пример 56. Для контроля срока службы электроламп из большой партии было отобрано 17 электроламп. В результате испытаний оказалось, что средний срок службы отобранных ламп равен 980 ч, а среднее квадратическое отклонение их срока службы 18 ч. Найти доверительный интервал для среднего срока службы с вероятностью 0,95.
Решение. По формуле 4.2 найдем доверительный интервал. По данным задачи 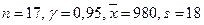 . По таблице Стьюдента находим
. По таблице Стьюдента находим 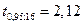 .
.
Тогда 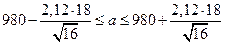 .
.
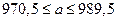 . То есть с надежностью 0,95 средний срок службы электроламп в партии заключен от 970,5 до 989,5 ч.
. То есть с надежностью 0,95 средний срок службы электроламп в партии заключен от 970,5 до 989,5 ч.
 2015-05-13
2015-05-13 2332
2332

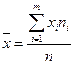 .
.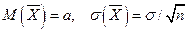 .
.