2015-05-13
821
Имеется статистическое распределение частот количественного признака Х.
Пусть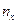 
– число наблюдений, при которых наблюдалось значение признака, меньшее х;
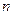– общее число наблюдений (объем выборки).
Относительная частота события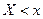 
равна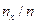 
.
Эмпирической функцией распределения называют функцию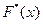 
, определяющую для каждого значения 
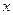относительную частоту события .
,
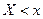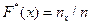где 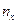число вариант, меньших 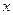; 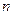– объем выборки.
Функцию распределения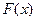 
генеральной совокупности называют теоретической функцией распределения.
Различие между эмпирической и теоретической функциями: теоретическая функция 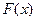определяет вероятность события 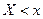, а эмпирическая 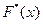определяет относительную частоту этого же события. При больших 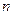эти числа 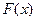и 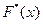мало отличаются друг от друга.
Свойства :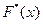
1) значение эмпирической функции принадлежит отрезку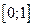 
;
2) 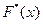– неубывающая функция;
3) если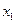 
– наименьшая варианта, то 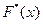=0 при 
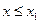; если 
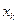– наибольшая варианта, то 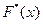=1 при 
.
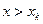Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
|
|
|
Пример 54. Построить эмпирическую функцию по данному распределению выборки:
| |||
| |||
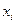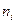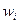| 0,2 | 0,3 | 0,5 |
Объем выборки равен 60.
Решение. Искомая функция распределения равна (рис. 5):
 |
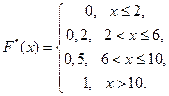
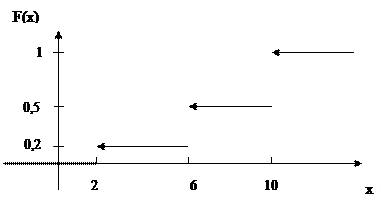Рис. 5. График функции распределения
