Шлифование сферических поверхностей

Шлифование алмазным трубчатым инструментом.

Инструмент устанавливают под углом а к оси вращения заготовки (рис. 2.25).

Одним инструментом, меняя угол а, можно обрабатывать сферические поверхности близкого радиуса R.

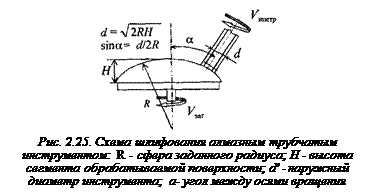Режущая кромка инструмента должна проходить через вершину детали или блока. Износ инструмента компенсируется подачей S_инстр. В результате обработки может быть получена выпуклая или вогнутая поверхности сферической детали с центром в точке пересечения осей вращения инструмента и детали.

Оборудование - специальные станки типа «Алмаз 70», и «Алмаз 250» (цифры означают максимальный диаметр детали или блока).

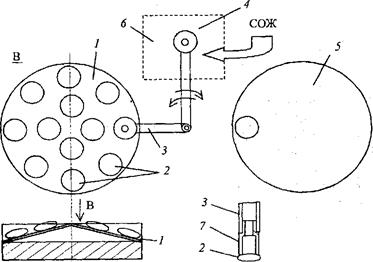Работа станка «Алмаз 70» схематично представлена на рис. 2.26.

	Рис. 2.26. Схема работы станка типа «Алмаз 70»

Подача заготовок-прессовок 2 в зону обработки 4 осуществляется автоматически. Прессовки 2 загружаются в вибробункер 1. Захватом 3, снабженным вакуум-присоской 7, прессовки переносятся в зону обработки 4, а после обработки - в бункер.

Шлифование свободным абразивом.

Инструмент 1 и приспосо ление 3 с заготовкой 2 вращаются на пересекающихся осях и образуют в результате сферу (рис. 2.27).

Рис. 2.27. Схема шлифования свободным абразивом

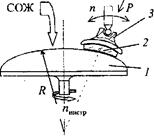Инструмент 1: чаша гриб. Способом обработки свободным абразивом и притиром достигается наилучшее совпадение формы реальной обработанной оптической поверхности с идеальной, т. е. геометрически заданной.

Способ принудительного шлифования.

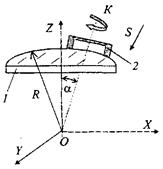В основе способа прину­дительного формообразования лежит геометрия простран­ственного пересечения двух тел: тонкостенного цилиндра 2, представляющего собой инст­румент, и заготовки 1. Оба тела жестко связаны с осями враще­ния (ОК и OZ), лежат в одной плоскости (ZOX) и пересекают­ся под углом а (рис. 2.28).

При вращении инструмен­та и заготовки и перемещения инструмента вдоль оси ОК кромкаинструмента вырезает в теле заготовки поверхность, все точки Которой лежат на окружности, образованной вращением относи­тельно оси ОК, и равноудалены от точки О. В то же время все точки Поверхности, вырезанной инструментом, также представляют тело вращения относительно оси OZ и равноудалены от точки О. Дан­ным геометрическим условиям удовлетворяет сфера, уравнение ко­торой в системе координат, связанной с заготовкой, имеет вид Х²+Y²+Z²=R², где R - радиус сферической поверхности детали.