Поверхности второго порядка: сфера, цилиндрические поверхности, эллипсоид, конус, гиперболоиды, параболоиды

Сфера - множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы.

- центр сферы

R - радиус

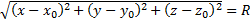
- уравнение сферы

 

 

Циллиндрическая поверхность

Пусть на хоу заданв прямая . Через каждую точку проведем прямые, параллельные оz. Эти прямые образуют поверхность, которую называют циллиндрической поверхностью.

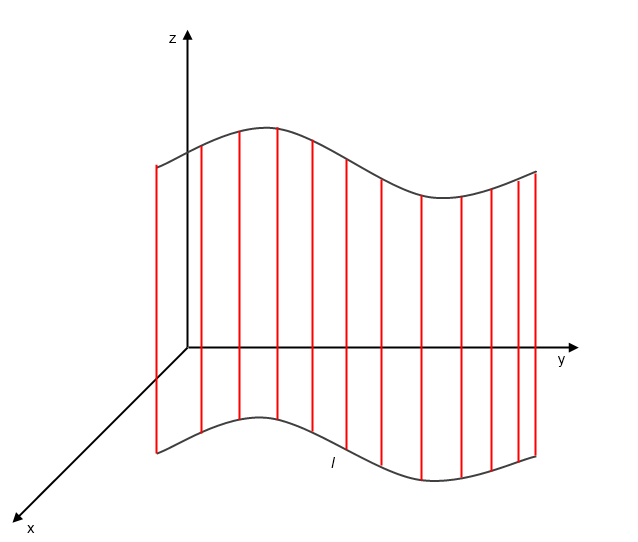
Кривая - направляющая

 

 

В зависимости от направляющей, выделяют три вида циллиндрических поверхностей:

I) -эллиптический циллиндр

II) - гиперболический циллиндр

III) - пара(барА-барА-парА-берЕ-берЕ)болический циллиндр

Эллипсоид

Эллипсоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением:

Конус -поверхность, заданная уравнением: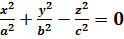

Гиперболоид

Однополостный гиперболоид определяется уравнением:

Двуполостный гиперболоид определяется уравнением: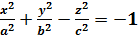

 

 

Параболоид

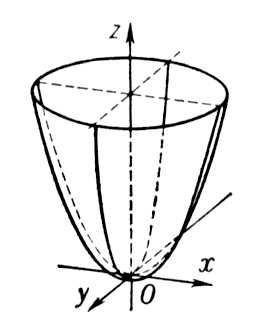
Эллиптический параболоид - поверхность, определяемая уравнением:

Матрицы, основные понятия и определения, сложение матриц, умножение матриц на число, умножение матриц, свойства этих операций; обратная матрица и правила её вычисления, ранг матрицы.

Матрицей размера m x n называется прямоугольная таблица, содержащая чисел, состоящая из m строк и n столбцов.

Элементы матрицы обозначаются , где - номер строки, в которой находится элемент, а - номер столбца.

Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний.

Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний.

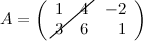
Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.

Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.

Ступенчатой называется матрица, которая содержит строк и у которой первые диагональных элементов ненулевые, а элементы, лежащие ниже главной диагонали и элементы последних строк равны нулю, то есть это матрица вида:

 

 

Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:

Операции над матрицами:

Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Суммой матриц и одного размера называется матрица такого же размера, получаемая из исходных путем сложения соответствующих элементов.

Свойства линейных операций:

Везде далее матрицы , и - матрицы одного размера.

1. Ассоциативность
2. , где - нулевая матрица соответствующего размера.
3. 
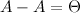
4. Коммутативность
5. Дистрибутивность
6. 
7. 

Произведением матрицы 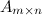на матрицу называется матрица такая, что элемент матрицы , стоящий в -ой строке и -ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -ого столбца матрицы .

Пример:

Задание. Найти , если

Решение. Так как , а , то в результате получим матрицу размера , т.е. матрицу вида . Найдем элементы данной матрицы:

Таким образом, получаем, что:

Все вычисления можно было сделать в более компактном виде:

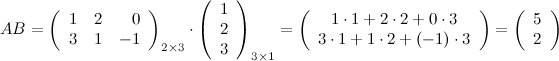
Ответ.

Свойства произведения матриц:

1. Ассоциативность
2. Ассоциативность по умножению
3. Дистрибутивность ,
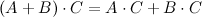
4. Умножение на единичную матрицу
5. В общем случае умножение матриц не коммутативно, т.е.
6. 

 

Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.

Квадратная матрица называется обратной к невырожденной матрице , если , где - это единичная матрица соответствующего порядка.

Свойства обратной матрицы:

1.

2.

3.

4.

 

Теорема. Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощью элементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.

Пример:

Задание. Для матрицы найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице справа единичную матрицу второго порядка:

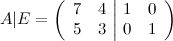
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

От второй строки отнимаем две первых:

Первую и вторую строки меняем местами:

От второй строки отнимаем две первых:

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что

Ответ.

Облегченный вариант:

Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:

Шаг 1. Находим определитель заданной матрицы, если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.

Шаг 2. Элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный.

Шаг 3. Делим все элементы на и получаем обратную матрицу.

 

Рангом матрицы называется ранг её системы строк или столбцов. Обозначается

На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.