2015-05-13
1324
Принимаем жесткость ригеля бесконечной, проверяем по формуле:
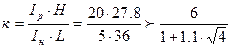
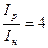
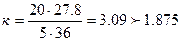- условие выполняется.
Так как ригель абсолютно жесткий принимаем углы поворота в точке В=0. А это значит в основной системе только одно неизвестное, это линейное перемещение.
Каноническое уравнение для определения смещения плоской рамы:
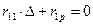
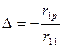
Определяем моменты от смещения верхних углов на ∆=1, используя таблицу 12.4 n=0.2, α=0.22.
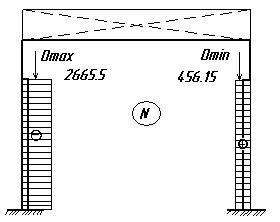
Расчетная схема:
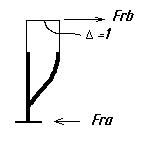
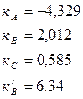
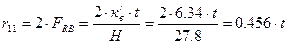
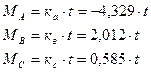
Строим эпюру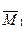 
:
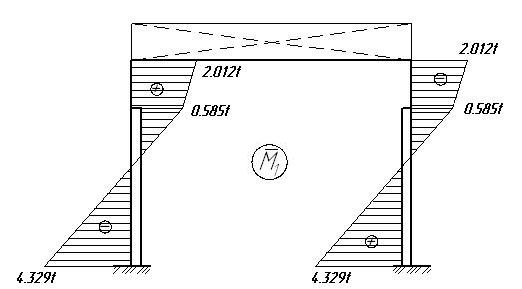
Строим эпюру Мр от внешней нагрузки Mmin, Mmax. По таблице 12.4 определяем коэффициенты kA, kB, kC, n=0.2, α=0.22.
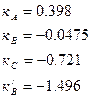
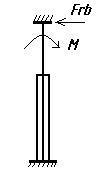
Моменты и реакции на левой стойке:
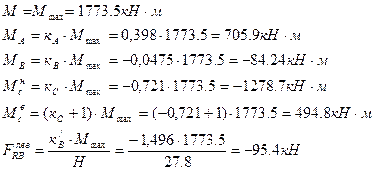
Моменты и реакции на правой стойке:
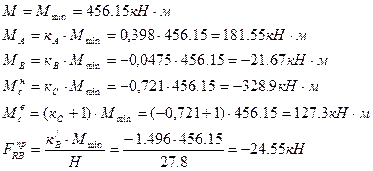
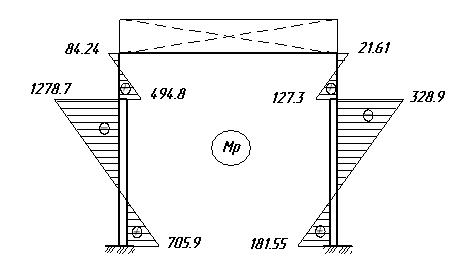
Реакции верхних концов стоек, кН:
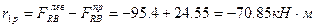
Из канонического уравнения определяем смещение плоской рамы:
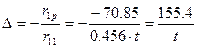
В расчете на крановые нагрузки следует учесть пространственную работу каркаса, определить αпр, ∆пр.
,
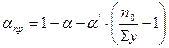где α и α’ – коэффициенты, принимаемые по таблице, в зависимости от коэффициента β.
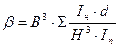
В=12м, Н=27.8 м,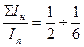 
при профилированном настиле 
, 
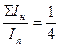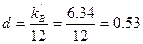
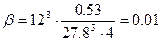
| β | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0. 1 | 0. 15 | 0. 2 | 0. 5 | |
| α | 0. 86 | 0. 77 | 0. 73 | 0. 71 | 0. 69 | 0. 67 | 0. 62 | 0. 58 | 0. 56 | 0. 46 |
| α’ | -0.144 | -0.2 | -0.22 | -0.24 | -0. 25 | -0. 25 | -0. 26 | -0. 26 | -0. 26 | -0. 26 |
α=0.77, α’=-0.2
n0 – число колес на одной нитке подкрановых балок, n0=8.
∑y – сумма ординат на линии влияния реакции опор, ∑y=4.91
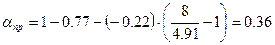
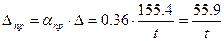
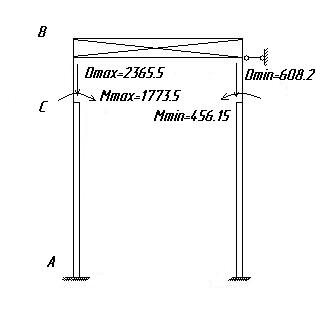
Строим эпюру моментов с учетом смещения ∆пр, т.е.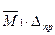 
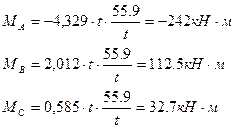
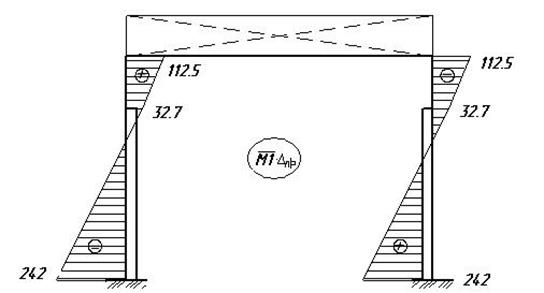
Строим эпюру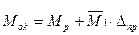 
Левая стойка:
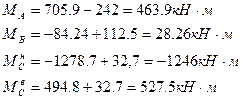
Правая стойка:
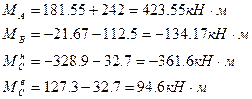
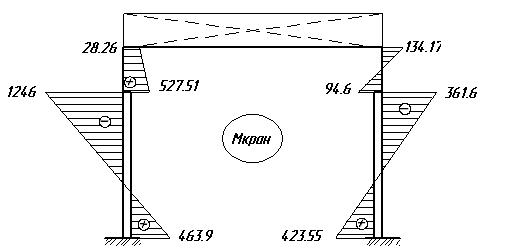
Проверка правильности построения эпюры Мкран. В точке С перепад эпюры на левой стойке равен моменту Мmax=1773.5кН*м: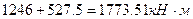 
, а на правой стойке равно Мmin=456.15 кН*м: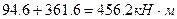 
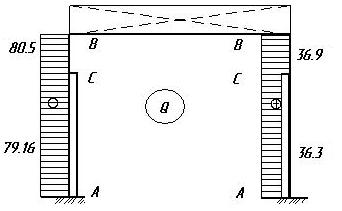
Строим эпюру поперечной силы Q, используя эпюру Мкран:
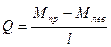при q=0
Левая стойка:
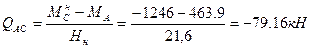
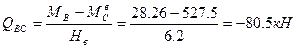
Правая стойка:
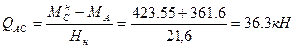
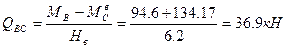
Поперечные силы на каждой стойке по участкам AC и BC равны:
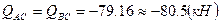- левая стойка
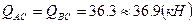- правая стойка
