Решение Блазиуса для ламинарного пограничного слоя. Другие решения

В случае установившегося ламинарного течения вдоль плоской пластины U ₁ = const, ¶ p /¶ x = 0, и уравнения (7.8), (7.9) сведутся к уравнениям пограничного слоя Прандтля.

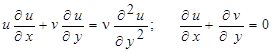, (7.28)

где выполняются граничные условия: на стенке y = 0, u = v = 0; вне пограничного слоя y ® ¥, u ® U ₁.

Предположим, что профили скорости вдоль пластины подобны при каждом x (автомодельны), тогда, согласно Блазиусу u / U ₁ = = F (y /d), u = U ₁ F (y /d), где функция F (y /d) - одна для всех x. Используем теперь функциональное соотношение (7.1) и предположим, что 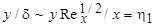. Введем функцию тока соотношениями .

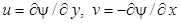Из первого из этих равенств имеем

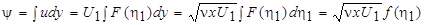. (7.29)

Подставив это выражение в первое уравнение (7.28) (второе уравнение функция тока удовлетворяет тождественно), для отдельных слагаемых получим:

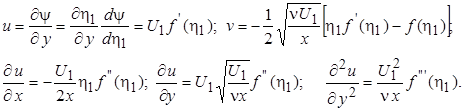
Тогда уравнение движения в пограничном слое (7.28) сводится к обыкновенному дифференциальному уравнению

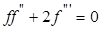, (7.30)

где .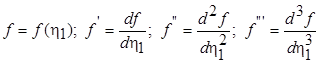

Граничные условия в новых переменных принимают вид:

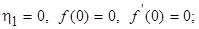(7.31)

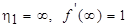. (7.32)

В настоящее время такие уравнения как (7.30) решают преимущественно на ЭВМ. Блазиус получил решение этого уравнения в виде разложения в степенной ряд в окрестности h₁ = 0. Этот метод хорошо известен из курса высшей математики, поэтому используем его для решения задачи.

Разложим неизвестную функцию 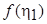- искомое решение – в ряд по 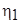вблизи точки :

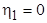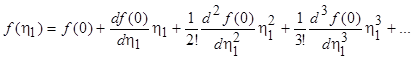(7.33)

Из граничных условий (7.31) имеем 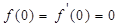и первые два коэффициента разложения равны нулю. Далее из уравнения (7.30) при 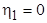получаем 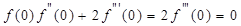, откуда после интегрирования находим .

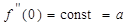Продифференцируем выражение (7.30) по 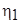и устремим 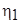к нулю, тогда 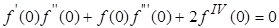. Учитывая полученные ранее результаты, находим 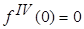. Еще раз повторив эту операцию, имеем 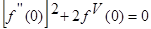или .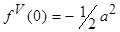

Описанная процедура продолжается до желаемой точности разложения. Если ограничиться разложением 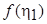до двенадцатого члена ряда включительно, то можно записать:

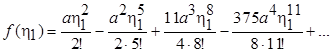(7.34)

Заметим, что это выражение удовлетворяет условиям .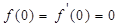

Константа a должна быть получена из граничного условия (7.32). Блазиус нашел ее, объединив разложение (7.34) с асимптотическим решением. Константа a может быть также оценена путем численного решения (интегрирования) уравнения (7.30), причем разложение (7.34) используется в качестве начального приближения для различных пробных значений 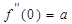. Обратная процедура заключается в подставке выражения (7.34) для f в уравнение (7.30), что формально приводит к линейному дифференциальному уравнению относительно f", имеющему решение

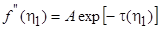, (7.35)

где 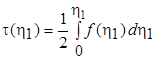и .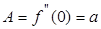

Условие для a записывается в виде

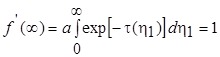. (7.36)

Выполнив действия в интеграле, определяющем 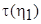, получим

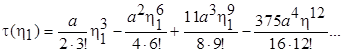(7.37)

Чтобы решить выражение (7.36) относительно а, необходимо вычислить интеграл, а для этого нужно выразить дифференциал d h₁ через решение (7.35), т.е. через t. Известно, что если имеется ряд

y = ax + bx ² + cx ³ + dx ⁴ + ex ⁵ +..., (a ¹ 0)

то коэффициенты обратного ряда

x = Ay + By ² + Cy ³ + Dy ⁴ + Ey ⁵ +...

будут равны:

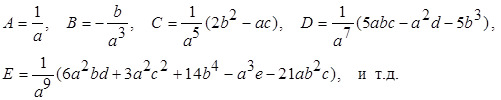
Сопоставляя выражение (7.37) с общим представлением "прямого" ряда y (x), видим, что y ~ t, a x ~ a h³/(2×3!). Тогда ряд (7.37) можно переписать в виде

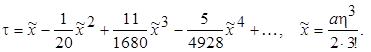
Следовательно, 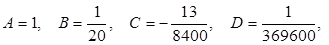и "обратный" ряд будет

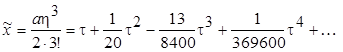
откуда находим

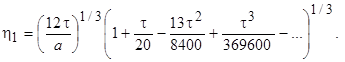
Используя разложения второго сомножителя в ряд Тейлора, окончательно получаем

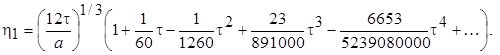
Дифференцируя это выражение и подставляя его в уравнение (7.36), получаем условие для определения а:

.

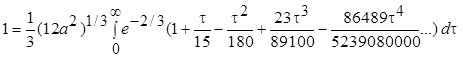Этот интеграл вычисляется либо аналитически (например, в рамках пакета Maple), либо численно одним из приближенных методов. Получаем

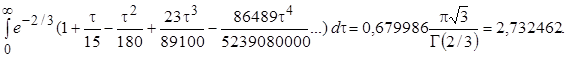
Тогда f ''(0) = a = 0,332093.

Располагая выражением для 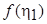, нетрудно рассчитать все параметры течения. Результаты вычислений для распределения продольного и поперечного компонента скорости приведены в табл. 7.1, из которой видно, что компонент скорости u очень быстро стремится к своему асимптотическому значению U ₁. Одновременно с этим наклон 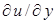стремится к нулю. Интересно отметить, что на внешней границе пограничного слоя компонента скорости v конечна, факт которого следовало ожидать из уравнения неразрывности и который вытекает из понятия толщины вытеснения. Заметим также, что вязкость n предполагается независимой от переменных интегрирования, т.е. подразумеваются, изотермические условия течения.

Таблица 7.1. Решение для установившегося ламинарного пограничного слоя на плоской пластине при нулевом градиенте давления в потоке

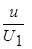		f (h1)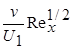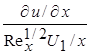
				0,3321
	0,3298	0,16557	0,0821	0,3230
	0,6298	0,65003	0,3048	0,2668
	0,8462	1,39682	0,5708	0,1614
	0,9555	2,30576	0,7581	0,0642
	0,9916	3,28329	0,8374	0,0159
	0,9990	4,27964	0,8572	0,00240
7,2	0,99996	5,47925	0,8604	0,00013
7,8	1,00000	6,07923	0,8604	0,00002
8,4	1,00000	6,67923	0,8604	0,00000

По полученным профилям скорости можно оценить толщину пограничного слоя 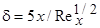при 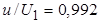. Отметим, что это согласуется с формой соотношения (7.1). Если использовать выражения (7.21) и (7.23), то толщина вытеснения и толщина потери импульса будут равны (в качестве верхнего предела интегрирования можно взять любое 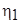, начиная с которого ):

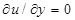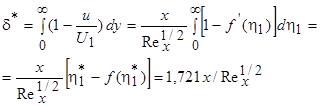(7.38))

где ;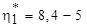

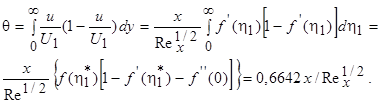(7.39)

Для местного касательного напряжения на стенке, которое определяется значением производной 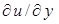на стенке, полученное решение дает

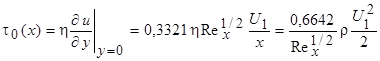. (7.40)

Тогда коэффициент местного касательного напряжения (локальный коэффициент трения), определяемый соотношением 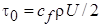, оказывается равным 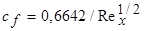. Подставив соотношение для толщины пограничного слоя в эту формулу, получим

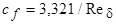. (7.41)

Обращает на себя внимание то обстоятельство, что толщина потери импульса q и локальный коэффициент трения c_f совпадают с точностью до текущей координаты пограничного слоя x, или, более точно, между ними существует соотношение q = c_f x. Такая связь, как станет ясно из дальнейшего, вообще справедлива для ламинарного пограничного слоя.

Полное сопротивление одной стороны пластины шириной b равно

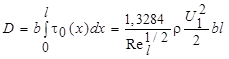. (7.42)

Используя соотношение 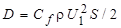, где площадь поверхности S = b×l, получаем

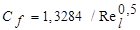. (7.43)

Все вышеприведенные теоретические результаты получены в предположении, что уравнения пограничного слоя справедливы при всех значениях х. Эксперименты показывают, что в непосредственной близости от передней кромки пластины имеет место зона, в которой полученные теоретические результаты не будут точны, так как величина d здесь не является малой в сравнении с х. Влияние этого обстоятельства на профили скорости и местные касательные напряжения становятся заметными при Re _x < 2×10⁴. Измерения профилей скоростей при больших числах Рейнольдса свидетельствует о хорошем согласии между теорией и экспериментом. Отметим также точность формулы толщины пограничного слоя.

Коэффициент местного напряжения 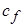может быть определен непосредственно измерениями силы, действующей на малую изолированную площадку поверхности стенки. Он может быть также вычислен по измеренным градиентам скорости около стенки на основе зависимости касательного напряжения для двухмерного пограничного слоя. Эксперименты, выполненные при больших числах Рейнольдса, показывают, что в обоих случаях полученные теоретические скорости и местные касательные напряжения очень хорошо согласуются с экспериментальными данными, свидетельствуя тем самым о точности теории как в математическом, так и физическом смысле.

Поскольку полное сопротивление представляет собой интеграл от местных касательных напряжений, вычисленных по всей площади пластины, то теоретический коэффициент, определяемый формулой (7.33), всегда будет содержать некоторую погрешность. Однако эта погрешность будет меньшей, чем погрешность определения локального коэффициента трения, т. к. операция интегрирования сглаживает (выравнивает) отклонения результатов теоретического расчета от экспериментальных данных. Как показывает сравнение результатов вычислений по формуле (7.33) с экспериментальными данными, эта погрешность становится пренебрежимо малой при .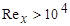

При анализе пограничных слоев используют понятие формпараметра 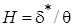. Как следует из решения Блазиуса, эта величина для ламинарного пограничного слоя не зависит от 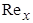, т.е. при любой скорости внешнего течения для всех жидкостей она постоянна и H =1,721/0,6642=2,59, если только в потоке отсутствует градиент давления.

При достаточно высоких числах Рейнольдса ламинарный пограничный слой становится неустойчивым. Малые возмущения усиливаются, что обусловливает переход к пограничному турбулентному слою.

Экспериментально установлено, что ламинарный пограничный слой на плоской пластине при отсутствии продольного перепада давления (U ₁ = const) устойчив при числах Рейнольдса меньших 8×10⁴. В инженерных расчетах, если не имеется другой информации (а тут пока незаменимы надежные опытные данные, полученные в рабочих услови­ях), обычно принимают, что переход от ламинарного по­граничного слоя к турбулентному происходит в диапазоне Re _x от 2×10⁵ до 5×10⁵.

Критерий перехода можно выразить и через толщину потери импульса. Предположим, что при обтекании плос­кой пластины потоком с (U ₁ = const) 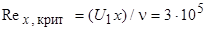. Для рассматриваемого случая 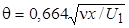. Исключая из последних двух соотношений x, получаем 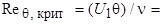360.

Это соотношение является местным критерием перехо­да от ламинарного пограничного слоя к турбулентному не­зависимо от предыстории пограничного слоя. Интересно отметить, что если для ламинарного течения в круглой тру­бе вычислить значения числа Re_q, у которого в качестве характерной скорости используется скорость на оси трубы, а в качестве характерного размера толщина потери им­пульса, то значению 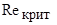=2000, основанному на средней скорости и диаметре трубы, соответствует 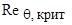=360. Таким образом, с этой точки зрения предложенный крите­рий удовлетворителен.

Турбулентный аналог течения Блазиуса можно постро­ить, допуская либо развитие ламинарного пограничного слоя до его самопроизвольного (спонтанного) перехода в турбу­лентный, либо путем искусственно вызванного перехода под действием сетки или других турбулизаторов. Однако при решении уравнений турбулентного пограничного слоя возникают две трудности, препятствующие применению мето­да анализа, развитого Блазиусом. Во-первых, уравнение количества движения содержит дополнительную зависимую переменную — турбулентное напряжение и, во-вторых, не­известен автомодельный профиль скорости для погранич­ного слоя, так как в ламинарной и турбулентной областях течения роль молекулярной вязкости существенно различ­на. Эту роль нельзя оценить одним параметром n, как это делалось для случая ламинарных течений.

Для слоя с постоянным давлением эти трудности несу­щественны, так как многие полезные результаты могут быть получены путем введения упрощений другого вида. В турбулентном потоке в трубе наибольшее изменение ско­рости имеет место в пристенном слое; это справедливо и для рассматриваемого пограничного слоя. Следователь­но, можно распространить профиль скорости пристенного слоя на внешнее течение, компенсируя это искусствен­ное допущение соответствующей модификацией эмпири­ческих констант в окончательных зависимостях.

Рассмотрим с этих позиций универсальный логарифми­ческий профиль скорости. Запишем его уравнение в виде

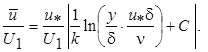(7.44)

Допустим, что при y = d, 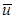= U ₁. Тогда

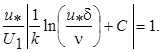(7.45)

Учитывая эти равенства, на основании определения (7.21) находим

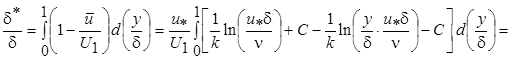
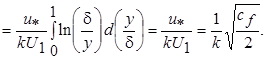(7.46)

Аналогичным образом, используя равенства (7.44), (7.45) и определение (7.23), получаем

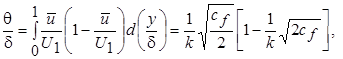(7.47)

тогда формпараметр

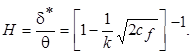(7.48)

Этот результат согласуется с приведенным ранее за­ключением, что автомодельное развитие турбулентного по­граничного слоя невозможно, за исключением предельного случая очень высоких чисел Рейнольдса, когда c_f очень ма­ло. Типичным является медленное уменьшение H по мере развития слоя и уменьшения c_f. Фактически это не очень точная оценка формпараметра, но она показывает, что изменение H в зависимости от c_f существенно; H =1,55¸1,2 для c_f =2×10^-2¸2,5×10^-3. Заметим, что эти результаты при­менимы для случаев гладкой и шероховатой стенок, т.к. они не зависят от постоянной С выражения (7.44).

Применяя логарифмический закон для внешней грани­цы пограничного слоя, получаем

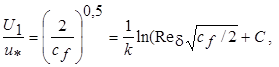
где Re_d = U ₁d/n.

Т. Карман, первым использовавший такой подход, пред­ложил формулу

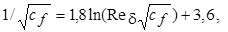(7.49)

которая соответствует эффективным значениям 1/ k _э = 2,55 и С _э = = 6,0. Из нее видно, что локальный коэффициент тре­ния для гладких поверхностей есть функция только числа Рейнольдса.

Формула (7.49) имеет своим недостатком то, что c_f в ней не выражается в ясном виде. Кроме того, толщину d, а поэтому и Re_d, трудно определить с достаточной точно­стью.

Толщина пограничного слоя зависит от расстояния х, измеряемого от передней кромки поверхности, и является функцией Rе _x. Предполагая, что пограничный слой турбу­лентен от самой передней кромки, Т. Карман преобразовал соотношение (7.49) и вычислил константы из прямых из­мерений местного касательного напряжения на стенке, по­лучив

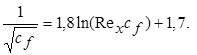. (7.49,а)

Эта формула достаточно точна, но и в ней c_f не выражает­ся в явном виде. Поэтому Шлихтинг сначала выполнил по уравнению (7.49, а) множество расчетов, затем аппроксими­ровал их формулой, в которой c_f уже выражено явно:

c_f = 1/(2lgRe _x – 0,65)^2,3.

Заметим, что этому выражению соответствует суммарный коэффициент сопротивления пластины шириной b и дли­ной l, определяемый по формуле

C_f =0,455/(lgRe _l)^2,58.

В литературе можно найти и другие выражения для ло­кального коэффициента трения. Наиболее часто в технических расчетах используют соотношения, основанные на так называемых степенных законах для профиля скорости и характеристики трения:

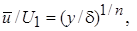(7.50)

и c_f = C ₁Re^{-1/ p}, (7.51)

причем п = 2 р - 1.

Подставляя выражение (7.50) в уравнения (7.21) и (7.23) после интегрирования получим

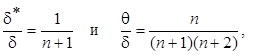(7.52)

откуда H = 1+2/ n. (7.53)

Сопоставление уравнений (7.48) и (7.53) дает зави­симость

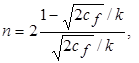
показывающую, что п = п (х) увеличивается вдоль слоя. Для c_f, изменяющегося в диапазоне от 0,01 до 0,0025, по­лучаются значения n = 4 ¸ 9, р = 3 ¸ 5 и H = 1,215 ¸ 1,547. В на­стоящее время значения коэффициентов, наиболее точно описывающих экспериментальные данные в диапазоне 5×10⁵ < Re _l < 10⁷, приняты в зависимостях

c_f = 0,059/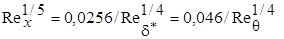

и

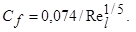
Заметим, что значению n = 7 соответствует следующая закономерность изменения толщины турбулентного погра­ничного слоя

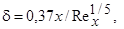
т.е. d увеличивается пропорционально х ^4/5, в то время как толщина ламинарного пограничного слоя увеличивается пропорционально х ^1/2.

Характеристики пограничного слоя, омывающего шеро­ховатую стенку, можно найти описанным выше способом на основе закона дефицита скорости. Для плоских и сла­боискривленных поверхностей он имеет вид:

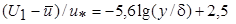при y /d £ 0,15;

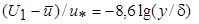при y /d > 0,15.

Уравнения для c_f применимы в случае, когда погранич­ный слой турбулентен почти с самого начала пластины. Поскольку на передней части пластины всегда имеется лами­нарный участок, то действительное сопротивление трения оказывается меньше определяемого по указанным урав­нениям. Согласно Прандтлю, в переходной области спра­ведливо выражение

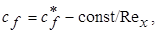
где с — коэффициент трения, определяемый уравнениями (7.49 - - 7.51), а const отыскивается экспериментально. В частности, для Rе _x < 10⁷, соnst = 1700.

Слои с неравномерным внешним течением

Решение Блазиуса является вариантом общего решения, соответствующего потенциальному потоку вне погранично­го слоя. Всякий раз, когда потенциальный поток вне пограничного слоя имеет вид 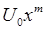или с 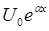с положи­тельным a, профили скорости в ламинарном пограничном слое при различных значениях х геометрически подобны. Для примера рассмотрим случай, когда 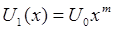. Это симметричный потенциальный поток, омывающий клин с углом при вершине pb, где b = 2 m /(m +1). Если m > 0, то поток ускоряется, и вершина клина x = 0 является точ­кой торможения. В случае m = 0 получаем равномерный поток, омывающий плоскую пластину, т.е. случай m = 0 соответствует решению, полученному выше. В случае за­медленного потока с m < 0 окрестности точки х = 0 долж­ны быть исключены из рассмотрения. В общем случае урав­нение Прандтля преобразуется с помощью соотношений

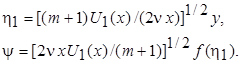(7.54)

Подстановка этих выражений в соотношения, связывающие компоненты скорости с функцией тока, и в уравнения Прандтля дает обыкновенное дифференциальное уравнение

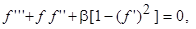(7.55)

известное как уравнение Фолкнера и Скэн. Граничные ус­ловия и = v = 0 при y = 0 и и / U ₁®1 при у ®¥ принимают вид

f (0) = f '(0) = 0, f '(¥) = 1. (7.56)

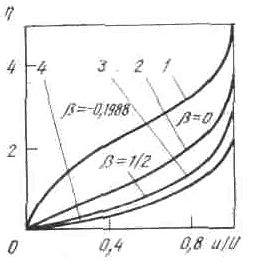Хартри численно проинтегрировал уравнение (7.55) и на­шел единственное решение для b > 0, m > 0; некоторые из них показаны на рис. 7.5. При 0 > b> - 0,1988 решения не являются единственными, если только ¦²(0) не выбрано так, чтобы ¦'(¥) наиболее быстро стремилось к единице. При b = - 0,1988 величина ¦²(0) = 0, так что (¶ и /¶ у) _{у =о}= 0 при всех значениях х. При b < - 0,1988 нет действи­тельных решений уравнений (7.55) и (7.56), при которых бы u экспоненциально стремилось к U ₁ и и / U ₁ < 1 при 0 < y <¥.

Рис. 7.5. Профили скорости в ламинарном пограничном слое при обтекании клина, когда b равно: 1 - - 0,1988; 2 – 0; 3 – ½; 4 – 1

Случай, когда b = 1, m = 1, т.е. случай двухмерного по­тока, натекающего на плоскую пластину по нормали к ней, характеризует течение в окрестности точки торможения на поверхно­сти малой кривизны. Случай b = ¹/₂, m = ¹/₃, т.е. двухмерного по­тока, омывающего клин с углом при вершине p/2, интересен, поскольку уравнение (7.55) при b = ¹/₂ может быть преобразовано в уравнение для осесимметричного потока в окрест­ности точки торможения на теле вращения.

Недостатком метода Блазиуса является необходимость рассмотре­ния большого числа членов ряда для очень многих профилей тел, пред­ставляющих практический интерес. Поэтому разработано множество других совершенных методов, обе­спечивающих большую точность. Со многими из них мож­но познакомиться по превосходным монографиям Д. Н. Ханта и Г. Шлихтинга.

Замечание. Весьма удобным средством решения краевых задач, подобных уравнению Фолкнера и Скэн, является распространённый ныне пакет Mathcad. В его составе имеется специальная команда sbval, позволяющая отыскать недостающие для сведения исходной краевой задачи к задаче Коши граничные условия. После установления этих условий можно использовать стандартный численный метод Рунге – Кутты, команда реализации которого также имеется в составе пакета.

Данная команда имеет шесть аргументов:

sbval (v, x1, x2, D, load, score).

Здесь:

v – вектор начальных приближений для искомых недостающих начальных условий в начальной точке x1 исследуемой области;

load(x1, v) – векторозначная функция, возвращающая значения граничных условий в точке x1. Эта функция включает n элементов, где n – порядок дифференциального уравнения;

score(x2, y) – количество элементов этой функции равно числу элементов вектора v. Каждый элемент содержит разность между граничным значением, заданным в конечной точке x2 исследуемой области, и значением решения в этой точке. Вектор score показывает, насколько значения найденного решения в точке x2 близки к значениям, заданным в этой точке граничными условиями. Значение 0 для любого элемента указывает на полное совпадение между заданным граничным условием и тем значением, которое возвращается функцией sbval;

D(x, y) – функция, возвращающая значения в виде вектора из n элементов, отображающих первые производные искомой функции.

Пример 7.2. Решить уравнение (7.55) для случая b = - 0,198858.

Уравнение Фолкнера и Скэн имеет третий порядок. Следовательно, для сведения краевой задачи (7.55), (7.56) недостаёт одного граничного условия, а именно f ''(0).

Ниже на рис. 7.6 представлена последовательность поиска этого условия и последующего решения задачи Коши в рамках пакета Mathcad. Чётко видно, что с погрешностью, не превышающей двух единиц пятого знака после запятой, функция sbval правильно определила недостающее граничное условие (должен быть 0).

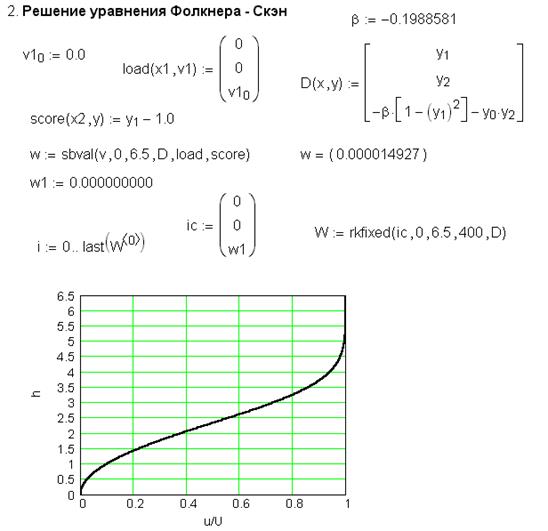
Рис. 7.6. Решение уравнения Флокнера и Скэн для b = - 0,198858

Теперь рассмотрим пограничный слой на цилиндрическом теле про­извольного поперечного сечения, обтекаемого двухмерным потоком, на­правление которого перпендикулярно оси тела. Для описания течения около цилиндра требуется представить функцию U ₁(х) в общем виде. Как и раньше, х и y - локальные координаты по касательной и норма­ли к поверхности тела. В этой задаче скорость потенциального течения около тела с затупленной передней кромкой представляется в виде сте­пенного ряда

,

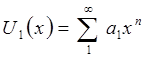критическая точка в этом случае имеет координаты x = y = 0. Для тела, симметричного относительно направления движения набегающего пото­ка, скорость U ₁ является нечетной функцией, х, т. е.

U ₁(x) = a ₁ x + a ₃ x ³ + a ₅ x ⁵ + ¼,

а известные коэффициенты a ₁, a ₃¼ зависят от формы тела. Следова­тельно

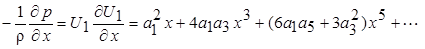(7.58)

Функцию тока y(x, у) для течения в пограничном слое можно записать в виде

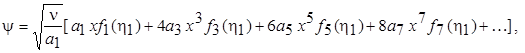, (7.59)

где h₁ = y (a ₁/n)^1/2. (7.60)

Ценность этого метода заключается в том, что f_i можно записать через функции, которые не зависят от 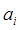, т. е. могут быть вычислены раз навсегда. Решение уравнений пограничного слоя для любого заданного тела тогда записывается через уже известные табулированные функции. Таблицы некоторых из них приведены в уже упоминавшейся работе Г. Шлихтинга.

Чтобы применить метод Блазиуса к потоку около кругового цилиндра радиуса r _о, запишем

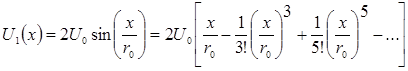, (7.61)

так что

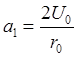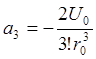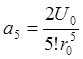, , и т.д.

Составляющая и (х, у) скорости в пограничном слое из уравнения (7.59) записывается в виде

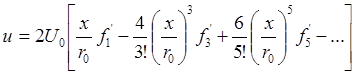(7.62)

Она представлена графически на рис. 7.7 для различных углов j = x / r ₀, измеряемых от критической точки. Если выражение (7.62) поставить в условие (¶ u /¶ y) _{y = 0} = 0, то в зависимости от числа учитываемых членов ряда (7.61) получим либо значение j_s= 109,5° (сохраняя четыре чле­на ряда), либо j_s=108,8° (при шести членах). Оба эти значения хо­рошо согласуются с экспериментальными данными, и можно заклю­чить, что применительно к этой задаче метод Блазиуса дает достаточ­но точное значение скорости в пограничном слое. Касательное напряже­ние t_о, вычисленное по уравнению (7.62), исчезает при j = 0 и j = j_s и возрастает до максимума при j»57°, где t₀» 4,5(r 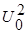/2)/(U ₀ r ₀/n)^1/2.

Определение координаты по длине пограничного слоя, в которой касательное напряжение на стенке становится равным нулю, представ­ляет огромный интерес, так как она непосредственно связана с поня­тием отрыва пограничного слоя.

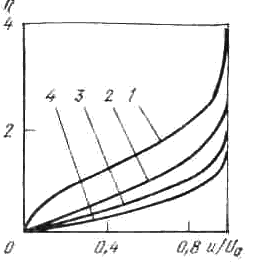
Рис. 7.7. Профили скорости в ламинарном пограничном слое на круговом цилиндре при угле j, град: 1 – 110; 2 – 90; 3 – 60; 4 – 0

Пример 7.3. В рассмотренных выше задачах одно из граничных усло­вий состояло в том, что нормальный к поверхности тела компонент скорости на самой поверхности был равен нулю, т. е. v ₀ = 0. Во многих технических устройствах это условие не выполняется. Например, в различных типах горелок и форсунок металлургических печей осуществля­ется вдув через проницаемую поверхность вторичного потока либо для защиты ее от разрушающего воздействия высокотемпературного главного потока, либо для обеспечения лучшего перемешивания топлива и воздуха. Другим примером может служить отсос пограничного слоя через пористую стенку для предотвращения его отрыва вследствие положительного (обрат­ного) перепада давления. В общем случае переменной скорости потенциального ядра потока исходным для анализа рассматрива­емой задачи является уравнение (7.55). Но­вое граничное условие по v ₀ = 0 можно найти следующим образом.

Из уравнений для потенциального по­тока и (7.54) следует, что

U ₁(x) = U ₀× x^m,

h₁ = y [(m + 1) U ₁(x)/(2n x)]^1/2,

y = [2n xU ₁(x)/(m + 1)]^1/2 f (h₁),

тогда

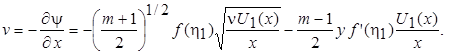
Но при у = 0 h₁ = 0 и v = v ₀. Следовательно,

.

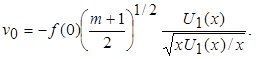Решая это уравнение относительно ¦(0) находим

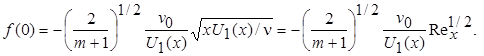
Совершенно очевидно, что при произвольном изменении v ₀ задачу можно решить лишь численно. Если положить ¦(0) = сопst, то методом разложения искомого решения в ряд по h₁ можно получить семейство автомодельных решений. Однако в этом случае v ₀ будет изменяться вдоль поверхности в соответствии с выражением

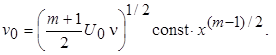
Ниже представлены некоторые решения уравнения (238) для слу­чая U ₁(x) = соnst (m = 0 - обтекание плоской поверхности).

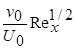	-2,500	-0,750	-0,250
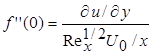	3,663	1,336	0,740	0,470
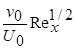	0,250	0,375	0,500	0,619
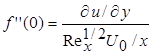	0,233	0,133	0,051

На рис. 7.8 показаны профили скорости для трёх значений (v ₀/ U ₀)´ ´ (Re _x)^1/2: - 0,750; 0 и 0,500. Можно видеть, что при отсосе поток "поджимается" к стенке, а при вдуве – напротив, отталкивается от неё.

h₁

Рис. 7.8. Профили скорости в ламинарном пограничном слое при отсосе газа (__), при вдуве (-.-.-) и в не- возмущённом потоке (_ _ _)

u / U ₀

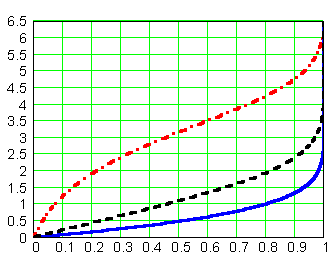
Ещё более наглядно различие поведения потока при отсосе и вдуве газа иллюстрирует распределение линий тока вблизи стенки (вертикальная координата на рис. 7.9; по горизонтали откладывается расстояние по толщине пограничного слоя в м).

Решение уравнений турбулентного пограничного слоя для произвольного градиента давления все еще представляет собой трудную задачу. В инженерной практике ее решают с использованием интегральной теоремы импульсов, при­ближенно удовлетворяя уравнениям пограничного слоя.

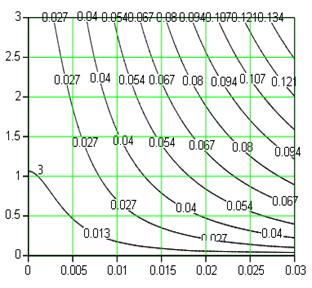
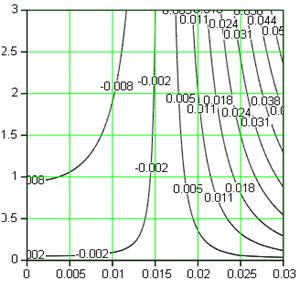
Рис. 7.9. Распределение линий тока в ламинарном пограничном слое при отсосе и вдуве части газа через проницаемую горизонтальную стенку длиной 3 м (скорость невозмущённого потока U ₀ = 5 м/с)