Уравнения движения в пограничном слое. Характерные толщины пограничного слоя

Прандтль показал, как можно упростить уравнение Навье - Стокса, проведя сравнительную оценку порядка величин входящих в них членов и опираясь при этом на основные представления о пограничном слое. Рассмотрим его результаты, полученные для двухмерного течения вдоль плоской пластины или слабо искривленной поверхности. Запишем уравнения Навье - Стокса, представленные в безразмерной форме, опустив влияние сил тяжести,

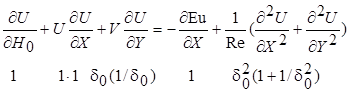; (7.4)

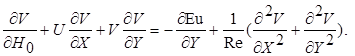(7.5)

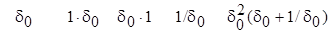
Для уравнения неразрывности имеем 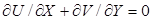. Во-первых, отметим, что пограничный слой является тонким и имеет малую кривизну и внутри этого слоя x >> y; u >> v; ¶ u /¶ y >> ¶ u /¶ x; ¶ p /¶ y - мало. Безразмерная толщина пограничного слоя d₀ = d/ L предполагается малой по отношению к единице: 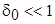. Исходя из этого, введем "шкалу" порядков величин

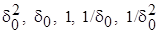. (7.6)

Для обозначения порядка величины используем символ ~ O. Тогда с помощью "шкалы" (7.6) представим относительные величины расстояний и скоростей следующим образом:

X ~ O(1); U ~ O(1); Y ~ 0(d₀). (7.7)

Для того чтобы течение имело четко выраженную структуру, в уравнении неразрывности должны сохраниться оба слагаемых. Поскольку ¶ U /¶ X ~ ~ 0(1), то из этого требования вытекает, что и ¶ V /¶ Y ~ O(1). Отсюда следует, что V ~ O(d₀), ¶² U /¶ X ² будет оставаться ~0 (1), в то время как ¶² V /¶ Y ² станет ~ O(1/d₀²). Иными словами, дифференцирование по Y увеличивает порядок величины, а дифференцирование по X - не изменяет его. Для того чтобы исключить случай больших ускорений, предположим, что ¶ U /¶Ho и ¶Eu/¶ X имеют тот же порядок, что и U ¶ U /¶ X, тогда Ho ~ O(1) и Eu ~ O (1).

Теперь для каждого из слагаемых уравнений (7.4) и (7.5) можно установить порядок величины (порядки величин показаны под соответствующими слагаемыми). При этом заметим следующее. Как видно из первого уравнения, для того чтобы удовлетворить постулату теории пограничного слоя, согласно которому внутри слоя вязкие силы должны быть сравнимы с силами инерции, число Рейнольдса должно быть весьма большим, т. е. иметь максимально возможный порядок величины 1/d₀². Из второго уравнения следует, что слагаемое ¶Eu/¶ Y, вообще говоря, отличное от нуля, вместе с тем на порядок больше всех остальных слагаемых. Но это означает, что в теории пограничного слоя ¶ p /¶ y = 0, т. е. давление потока в направлении, перпендикулярном поверхности, остается неизменным.

Опуская в уравнении (7.4) все слагаемые, порядок которых меньше единицы, и возвращаясь к размерным выражениям, получим уравнения Прандтля для двухмерного пограничного слоя:

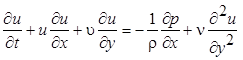; (7.8)

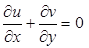. (7.9)

Они должны удовлетворять следующим граничным условиям:

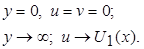(7.10)

Отметим, что пренебрежение одним из учитывающих напряжение слагаемых высшего порядка 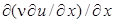имеет вполне определенную физическую интерпретацию. Такое упрощение допускает то, что движение в пограничном слое не зависит от условий ниже по течению; следовательно, его поведение можно рассчитать с помощью одного интегрирования вдоль потока, при котором учитывается "история" течения, а не его "будущее".

На внешней границе пограничного слоя (в ядре потока), как уже отмечалось ранее, влиянием сил вязкости можно пренебречь, и закономерности движения должны хорошо соответствовать картине потенциального течения. Учитывая также, что давление p постоянно по сечению пограничного слоя и поэтому равно давлению во внешнем потоке, где u = U ₁(x), v = 0 (это условие является неточным, так как из уравнения (7.9) следует, что при y ® ¥, v = - ò(¶ U ₁/¶ x) dy ¹ 0. Данный источник погрешности теории пограничного слоя не приводит к заметному изменению профиля скорости u и, в особенности, к ошибкам в определении интегральных характеристик течения), можно записать

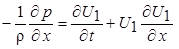, (7.11)

тогда уравнение

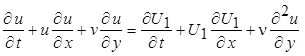. (7.12)

Полученные выше уравнения пограничного слоя можно применять к задаче обтекания криволинейной поверхности двумерным потоком. В этом случае (x, y) надо рассматривать как соответствующую систему криволинейных координат, образованных границей тела и кривыми, параллельными ей, а также нормалями к этой границе (рис. 7.1). На кривизну поверхности необходимо наложить следующие ограничения: радиус кривизны должен быть большим по сравнению с толщиной пограничного слоя и должны отсутствовать резкие изменения кривизны, какие имеют место на углах тел.

Пример 7.1. Простейшим примером трехмерного пограничного слоя является слой в вязком потоке, обтекающем тело вращения, когда невозмущенный поток параллелен оси тела (осесимметричен). Поскольку необходимо рассматривать только два компонента вектора скорости, то эту задачу легко преобразовать в соответствующую для двухмерного течения.

В этом случае уравнение (7.12) остается верным, если под (x, y) понимать локальные координаты (см. рис. 7.3). Однако уравнение неразрывности (7.9) изменится, так как в нем должна найти отражение геометрия обтекаемой поверхности. Для тела вращения имеется один дополнительный параметр – локальный радиус вращения r ₀(x). Рассматривая уравнение баланса массы жидкости, получим .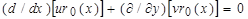

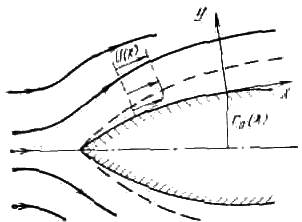
Рис. 7.3. Схема пограничного слоя на криволинейной стенке (поверхности вращения)

Это уравнение неразрывности можно тождественно удовлетворить, если функцию тока ввести соотношениями .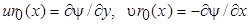

Уравнения пограничного слоя (7.9) и (7.10) справедливы как для ламинарного, так и для турбулентного течений. Однако применительно к последнему случаю целесообразно записать их в виде, учитывающем статистический характер компонентов скорости и давления потока. Указанную форму записи уравнений турбулентного пограничного слоя можно получить либо путем подстановки мгновенных значений u, v, p и последующего усреднения, либо из уравнений Рейнольдса, выполняя анализ значимости отдельных слагаемых аналогично тому, как это было сделано выше. Используя любой из этих способов, находим для несжимаемой жидкости (газа)

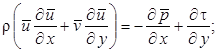(7.13)

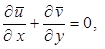(7.14)

где касательное напряжение в плоскости xy

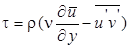. (7.15)

Помимо законов сохранения массы (7.14) и количества движения (усредненного) (7.13) в турбулентном пограничном слое должен выполняться законом сохранения интенсивности турбулентности (см. гл. 6):

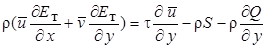, (7.16)

где ;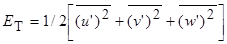

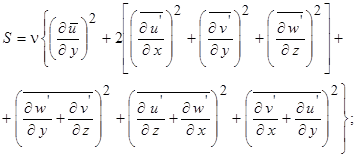(7.17)

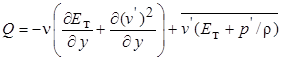. (7.18)

Последние два слагаемых уравнения (7.16) характеризуют диссипацию кинетической энергии турбулентности, т. е. ее переход в тепловую энергию, которая рассеивается в окружающую среду. Заметим, что в этом уравнении фигурируют все три пульсационные составляющие скорости потока, так как турбулентность является по существу трехмерным явлением.

Уравнения пограничного слоя (7.13), (7.14) и (7.16) следует решать таким образом, чтобы удовлетворились граничные условия:

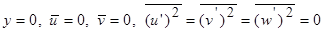; (7.19)

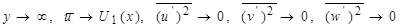. (7.20)

Нетрудно заметить, что количество неизвестных, содержащих в этих уравнениях больше числа уравнений. Поэтому для решения необходимо сделать дополнительные предположения. В частности, прежде всего необходимо найти распределение средней скорости 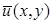в пограничном слое и принять некоторые гипотезы относительно величин 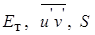и .

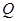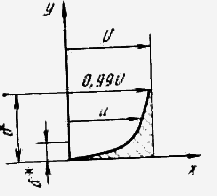Толщина пограничного слоя d не может быть установлена точно, так как точка, отделяющая пограничный слой от зоны с пренебрежимо малым влиянием вязкости, не является отчетливо выраженной. Поэтому обычно определяют d как расстояние от стенки до точки, где скорость отличается от скорости внешнего потока на некоторую долю последней (обычно на 1%).

Рис. 7.4. Схема для определения толщины вытеснения(заштрихованная площадь равна d^* U = ò(U – u) dy)

Как уже отмечалось ранее, уменьшение скорости в пограничном слое вызывает "дефицит" потока массы вблизи границы по сравнению с потоком массы, который прошел бы через ту же самую зону при отсутствии пограничного слоя. Это положение иллюстрируется на рис. 3.4. Согласно уравнению неразрывности этот "дефицит" потока массы эквивалентен смещению ("вытеснению") линии тока на внешней границе пограничного слоя на определенную величину, известную как толщина вытеснения d^* и определяемую равенством:

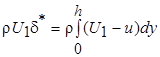(7.21)

или

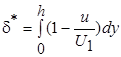, (7.22)

где h ³ d. Эти уравнения показывают, что d^* представляет собой толщину воображаемого слоя жидкости, движущегося со скоростью U ₁, поток массы в котором равен "дефициту" потока массы. Толщина вытеснения может быть определена со значительно большей точностью, чем полная толщина d.

Замедление течения внутри пограничного слоя вызывает соответствующее уменьшение потока импульса (или количества движения). Определим толщину потери импульса q как толщину воображаемого слоя жидкости, движущегося со скоростью U ₁, поток импульса в котором равен "дефициту", вызванную замедлением потока у стенки. Толщина потери импульса

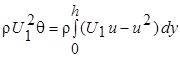(7.23)

или

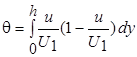. (7.24)

Толщины вытеснения и потери импульса характеризуют как ламинарный, так и турбулентный пограничные слои. Необходимо только при расчетах турбулентного течения в выражениях (7.21), (7.23) компонент скорости u заменить на 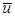. Кроме того, при анализе турбулентного пограничного слоя полезно понятие толщины потери энергии:

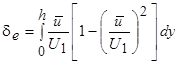. (7.25)

Решение уравнений ламинарного пограничного слоя не вызывает затруднений при использовании численных методов анализа. Решение уравнений турбулентного пограничного слоя для произвольного изменения давления в ядре потока остается до сих пор весьма затруднительным даже после того, как сделаны какие-то произвольные предположения относительно турбулентного касательного напряжения и других величин. Обычно, учитывая структуру пограничного слоя (см. гл. 6), граничные условия на поверхности тела (210) заменят следующими

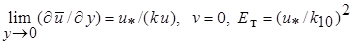, (7.26)

где k = 0,4; а k ₁₀ = 0,56. Обе эти постоянные определены из эксперимента. В настоящее время их считают универсальными постоянными.

Турбулентное напряжение трения может быть взято из теории пути смешения (гл.6). Согласно более позднему предположению Прандтля коэффициент турбулентного обмена количеством движения (вихревая кинематическая вязкость) пропорционален результирующей пульсационной скорости

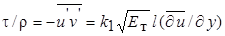. (7.27)

Далее Прандтль принимает, что 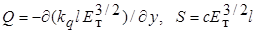, где l - характеристическая длина. Около стенки l = ky. В этом случае l идентична пути смешения. Следовательно, вблизи стенки имеем логарифмический профиль средней скорости. Постоянные k ₁, k_q и c могут быть определены из условий на внешней границе вязкого (ламинарного) подслоя. Как правило, их находят экспериментально.