Динамика затопленной струи

Основной задачей анализа струйного течения является оп­ределение полей скоростей и расходов по длине и сечению струи, ее границ и угла раскрытия, количества движения и кинетической энергии, поскольку величиной указанных параметров определяется характер теплового и механиче­ского воздействия струи на обрабатываемые материалы.

Рассмотрим развитие струи, истекающей из длинной щели шириной 2 b ₀ (рис. 6.8). Воспользуемся упрощенной схемой струи, представив длину переходного участка рав­ной нулю. В этом случае сечение, в котором сопрягаются начальный и основной участки, называют переходным сече­нием струи. Если в расчетах переходной участок учитыва­ют, то переходное сечение считают совпадающим с нача­лом основного участка. Основные соотношения для пере­носа количества движения в области полностью развитой струи можно вывести из упрощенного уравнения движения.

Проинтегрируем уравнение Прандтля по у и получим

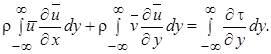(10.2)

Порядок дифференцирования и интегрирования в первом слагаемом этого выражения можно изменить, учитывая, что 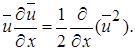Кроме того, второе слагаемое может быть проинтегрировано по частям

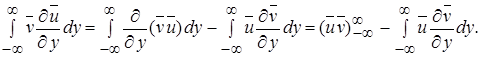(10.3)

В результате получаем

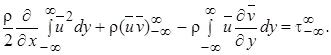(10.4)

Согласно уравнению неразрывности ¶ 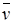/ ¶ у =¶ и/ ¶ х, поэтому третье слагаемое левой части выражения (10.4) мо­жно переписать в виде:

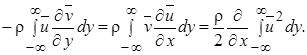
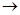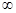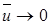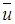При у (± ) и ¶ / ¶ у 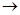0. Следовательно, второе слагаемое левой части уравнения (10.4) и касательное на­пряжение 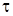равны нулю. Таким образом, выражение (10.4) можно записать в виде:

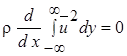или 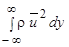= const. (10.5)

Физический смысл этого равенства становится очевид­ным, если вспомнить, что произведение 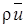есть количество движения (импульс) единицы объема, а udy в случае пло­ской струи - элементарный объемный расход потока. Сле­довательно, интеграл от выражения 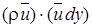- полное количество движения, проходящее в единицу времени че­рез некоторое сечение струи.

Из соотношения (10.5) следует, что поток количества движения в струе постоянен и не зависит от х. Это являет­ся следствием предположения о постоянстве давления, так как в этом случае результирующая внешних сил, действую­щих на некоторый контрольный объем, заключающий в себе струю газа, равна нулю, и поток количества движения вдоль струи остается постоянным.

Константу в выражении (10.5) можно вычислить, зная поток количества движения при х = 0. Действительно, если количество движения единицы объема равно 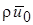и объем­ный расход равен 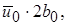то

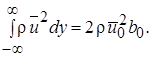(10.6)

В области полностью развитой струи b и осевую ско­рость струи 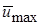можно выразить как функцию от х в ви­де степенных законов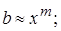 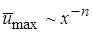. Используя эти соотношения, а также уравнение нераз­рывности, можно выразить порядок величин различных сла­гаемых уравнения движения Прандтля:

1)

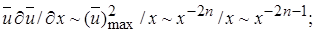
2)

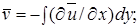
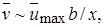
откуда

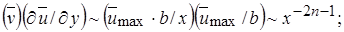
3) 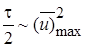и

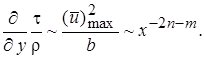
Поскольку левая часть уравнения Прандтля имеет по­рядок 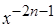и правая часть - 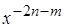, то, следовательно, 2 n + 1 = 2 n + m, откуда m = 1. Левая часть равенства (10.5), которое выражает постоянство потока количества движе­ния, по такой же оценке имеет порядок 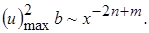Поскольку m = 1, равенство (10.5) может выполняться для любых х лишь при показателе степени, равном нулю и, сле­довательно, n = ½.

Таким образом, проведенный анализ позволяет заклю­чить, что плоская струя расширяется по линейному закону в функции расстояния от сопла, а осевая скорость умень­шается как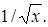

Число Рейнольдса струи может быть определено по её ме­стной ширине и осевой скорости: 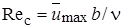. Поскольку эта величина имеет порядок 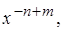или 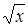, число Рейнольдса возрастает с расстоянием. Практически число Рейнольдса может возрастать лишь до тех пор, пока размеры струи не достигнут границ объема (пространства), в кото­рый она втекает.

Вышеприведенное рассуждение дает некоторое общее представление об основных чертах процесса распростране­ния струи, однако оно не дает ответа на основной вопрос о профиле скорости, интенсивности подсасывания окружа­ющего газа и действительных размерах струи. Для ответа на этот вопрос было развито несколько полуэмпирических подходов, базирующихся на предположении о геометриче­ском подобии профилей скорости в области полностью раз­витой струи. Условия подобия выражаются в виде

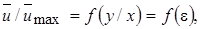(10.7)

где 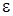= у / х.

Ниже излагается для случая плоской струи один из та­ких методов, в котором предполагается, что подобные про­фили скорости представляют собой гауссовские кривые вида

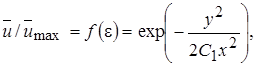(10.8)

где 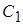- константа, определенная экспериментально. В со­ответствии с выражениями (10.6) и (10.7) условие постоян­ства потока количества движения принимает вид

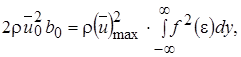(10.9)

или

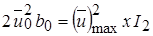, (10.10)

Следовательно, отношение осевой скорости к начальной ско­рости струи 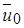можно выразить следующим образом:

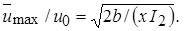(10.11)

Длину потенциального ядра L ₀ можно найти, зная, что для начального участка 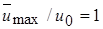и, следовательно, L ₀ =2 b ₀/ I ₂. Полный объемный расход на единицу ширины струи для x > L ₀ можно получить интегрированием местной ско­рости по сечению струи:

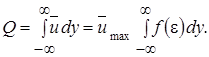
Зная, что начальный расход не единицу ширины 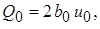отношение полного расхода к начальному расходу может быть выражено в функции от 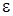т.е.

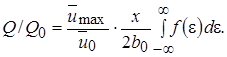
Используя выражение (10.11) и обозначая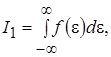

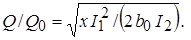(10.12)

Экспериментальные результаты Альбертсона с сотрудника­ми и ряда других исследователей показывают, что распре­деление скорости вида (10.8) удовлетворяет измеренному распределению в турбулентной струе, если C ₁ = = 0,109, от­куда I ₁ = 0,272, I ₂ = 0,192, а 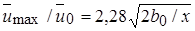при x > L ₀; L ₀ =10,4 b ₀ ; Q / Q ₀ = 0,62 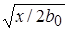при x > L ₀ .

Опыты показывают, что плоская струя может рассмат­риваться как турбулентная, если число Рейнольдса, вычис­ленное по начальной скорости и ширине щели, больше чем 30.

Аналогичным образом выполняется анализ закономерно­стей развития осесимметричной (круглой) затопленной струи. Заметим, однако, что изменение геометрии потока приводит к отличиям результирующих характеристик такой струи по сравнению с рассмотренной выше плоской. Прежде всего это относится к уравнению сохранения количества движения (10.6), которое для круглой струи имеет вид

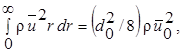(10.13)

где r соответствует b (рис. 6.8). Изменяется в данном слу­чае и характер убывания осевой скорости u _max. Если осевая скорость плоской струи уменьшалась обратно пропорцио­нально 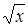, то у круглой струи 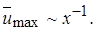Поскольку закономерность нарастания толщины (радиуса) струи оста­ется прежней 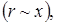то отсюда вытекает свойство осесимметричной струи сохранять постоянство турбулентного касательного напряжения на ее оси.

В самом деле, если вычислять число Рейнольдса по ло­кальному радиусу струи и скорости на ее оси, то получим 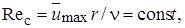что свидетельствует о постоянстве турбулентных характеристик потока.

Соотношения для определения профиля скорости и из­менения осевой скорости в продольном направлении для основного участка осесимметричной струи запишутся в виде:

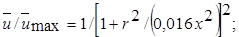(10.14)

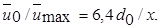(10.15)

Поскольку расширение струи происходит с ростом х ли­нейно, то можно говорить об угле расширения. При этом следует учитывать, что струя расширяется конически, как это показано на рис. 6.8. Для линии, вдоль которой 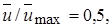угол расширения равен 6,5^o для плоской струи и 5^o для круглой струи. Вершина конуса для плоской струи лежит в центре сопла, а для осесимметричной отсто­ит от сопла по оси струи на расстояние 0,6 d ₀ .

В соответствии с формулой (10.15) струя является уже полностью развитой, начиная с сечения x = 6,4 d ₀ , и, сле­довательно, длина начального участка L ₀ = 6,4 d ₀ + 0,6 d ₀ = 7 d ₀. При выводе формул (10.14) и (10.15) была использо­вана эмпирическая зависимость для коэффициента вихревой вязкости 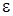в виде 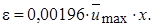Подставляя в это со­отношение значение максимальной скорости из уравнения (10.15) найдем, что 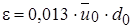или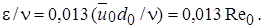

Полагая, что из сопла диаметром d ₀ = 3 см вытекает струя воздуха с начальной скоростью 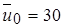м/с в воздух при "нормальных" условиях, получаем Re₀ = 62000 и 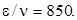Таким образом, вихревая вязкость в этом случае почти в тысячу раз больше молекулярной вязкости. Тече­ние в круглой струе становится ламинарным 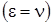при числе Re < 80.

Опыты показывают, что профиль скорости осесиммет­ричной струи довольно хорошо аппроксимируется также гауссовской кривой, как это предполагалось в анализе для плоской струи. Однако гауссовская кривая дает скорости, которые являются слишком малыми вблизи границ круглой струи (рис. 10.2).

Примечателен экспериментальный факт о том, что в осесимметричной турбулентной струе полностью развитое турбулентное течение наблюдается лишь в области ядра вплоть до радиуса, на котором 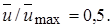Вне этого ядра лежит довольно широкая кольцевая переходная область,. а за ней до границ струи течение носит характер ламинар­ной оболочки.

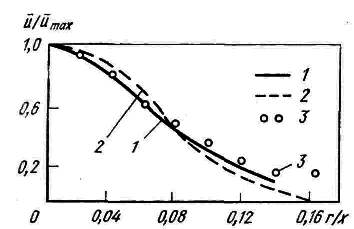
Рис. 10.2. Аппроксимация профиля скорости осесимметричной струи гауссовской кривой (2): 1 - эксперимент; 2 - расчет

В качестве количественной характеристики переходной области можно использовать коэффициент перемежаемости 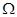(см. гл. 4). В полностью турбулентной области 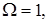а в нетурбулентной области 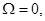На рис. 10.3 представлен. профиль величины коэффициента перемежаемости по сече­нию круглой турбулентной струи. Если скорость равна 0,1 от величины осевой скорости, то поток является турбулент­ным в течение примерно половины времени.

W×10

Рис.6.3. Изменение коэффициента пере- межаемости по ширине струи: 1 – x / d ₀ =

= 20; 2 – 27; 3 – 37; 4 – 64,5; 5 - 76

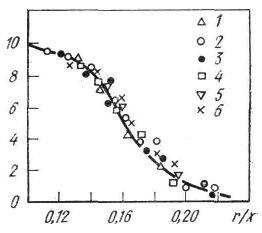
Количество жидкости, подсасываемой круглой струёй, можно определить путем интегрирования профилей скоро­сти в основном участке. Объемный расход в струе тогда. выражается простой формулой:

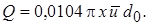
Поскольку

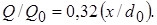
Подобный же расчет, основанный на гауссовской кри­вой, дает менее точный результат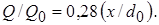

Поскольку вследствие подсоса окружающей среды скорость на оси струи непрерывно уменьшается, то можно говорить о длине струи. Обычно за длину струи принимают такое расстояние от среза сопла, начиная с которого скоро скорость на её оси становится меньше некоторой заданной доли скорости истечения (как правило, 5 ¸ 10%).

Для описания универсальных (автомодельных) профи­лей скорости в основном участке осесимметричной или пло­ской затопленной струи могут быть подобраны приближен­ные аналитические зависимости. Например, для воздушной струи можно пользоваться функцией 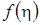, которую впервые теоретически получил Шлихтинг:

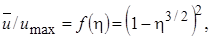(10.18)

где 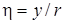- расстояние от точки до оси струи со скоро­стью u, выраженное в долях от радиуса (или полутолщи­ны) струи. Например, для точки 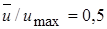относительное расстояние 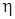легко определяется из выражения (383): 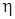= y / r = 0,441. Для неизотермических струй можно пользо­ваться соотношением, полученным С.И. Авериным на ос­нове оригинального теоретического подхода к описанию яв­лений свободной турбулентности:

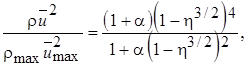(10.19)

где 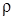_mах - концентрация смеси газовых сред струи и окру­жающего пространства на оси; 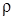- то же в любой другой точке поперечного сечения струи; 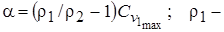начальная плотность газовой среды; 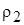- плотность окру­жающей среды; 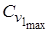- концентрация истекающей газовой среды струи на оси. Для затопленной струи 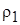= 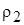, и выра­жение (10.19) трансформируется в уравнение Шлихтинга (10.18). Профили скорости, рассчитанные по этим формулам, хорошо согласуются с экспериментальными профилями ско­рости (рис. 10.1).

Представленный выше анализ закономерностей разви­тия затопленных струй характерен в двух отношениях. Во-первых, он дает физическое описание струйного течения, вводит понятия и терминологию, а также устанавливает структуру (схематическое строение) турбулентной струи, которая в своих основных чертах сохраняется практически при любом типе взаимодействия струи с окружающей сре­дой. Во-вторых, данный анализ наглядно показывает, что в математическом плане турбулентная струя определяется, по сути дела, двумя функциями: распределением скорости по поперечному сечению струи (профилем скорости) и из­менением осевой (максимальной) скорости вдоль потока. Именно эти две функции служат основой для последую­щего расчета коэффициентов тепло- и массообмена между газом и обрабатываемым материалом, процесса факельного горения топлива и т. д. Отметим также то обстоятельство, что закономерности нарастания толщины затопленной струи не зависят от ее геометрии и для основного участка подчи­няется простой зависимости b = c x.

Пример 10.1. Определить длину плоской и осесимметричной струй для одинаковых значений b ₀ и d ₀.

В соответствии с выражением (10.11) для плоской струи 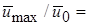= 2,28(2 b ₀/ x)^1/2. Принимая 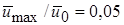, получаем

L _oсн/ b ₀ = 2×(2,28/0,05)² = 4158,72.

Прибавляя длину начального участка, окончательно находим

L _c = L _осн + L ₀ = 4158,72 b ₀ + 10,4 b ₀ = 4169,12 b ₀.

Аналогичным образом, на основании выражения (10.15) имеем

L _осн = 6,4/0,05 d ₀ = 128 d ₀

и

L _c = 128 d ₀ + 7 d ₀ = 135 d ₀.

Столь резкое различие в длинах струй объясняется тем обстоятельством, что плоская струя подсасывает окружающую среду лишь в направлении оси у (сверху и снизу), в то время как в осесимметричной струе подсос осуществляется по всему периметру поперечного сечения.