Перемещение среды, в которую вытекает струя, параллельно оси струи приводит к увеличению интенсивности турбулентного обмена количеством движения между двумя потоками. В результате изменяются закономерности подсоса окружающей среды в струю, а также протяженность последней. В то же время, нет оснований полагать, что это обстоятельство существенно сказывается на структуре струи и на распределение скорости в ее поперечном сечении. Поэтому принято считать, что при любой скорости внешнего потока 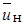 профиль скорости в основном участке описывается функцией Шлихтинга (10.18), которая в данном случае имеет вид:
профиль скорости в основном участке описывается функцией Шлихтинга (10.18), которая в данном случае имеет вид:
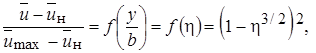 (10.20)
(10.20)
а профиль скорости в начальном участке 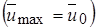 - кривой универсальной скорости:
- кривой универсальной скорости:
 (10.21)
(10.21)
Здесь безразмерная ордината 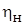 отсчитывается от наружной границы струи у 2:
отсчитывается от наружной границы струи у 2:
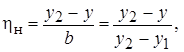 (10.22)
(10.22)
где y 1 —координата внутренней границы пограничного слоя.
Таким образом, задача определения параметров турбулентной струи, развивающейся в спутном или встречном потоках, сводится к установлению закономерностей расширения границ струи и изменения ее осевой скорости.
Указанная задача может быть решена на основе теории пути смешения Прандтля. В этой теории (см. гл. 6) Прандтль полагал, что пульсационные составляющие продольного и поперечного компонентов скорости пропорциональны изменению средней скорости в направлении, перпендикулярном направлению движения потока 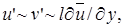 где l - длина пути смешения (гл. 6).
где l - длина пути смешения (гл. 6).
Как уже указывалось ранее, скорость расширения струи (скорость нарастания толщины пограничного слоя) определяется, главным образом, пульсационной составляющей поперечного компонента скорости, т.е. 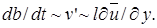 В случае осесимметричной струи вместо b следует подставлять ее радиус r.
В случае осесимметричной струи вместо b следует подставлять ее радиус r.
Подобие профилей скорости в различных сечениях пограничного слоя позволяет считать, что 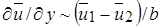 или
или 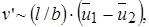 где
где 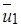 и
и 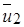 - скорости на внутренней и внешней границах пограничного слоя.
- скорости на внутренней и внешней границах пограничного слоя.
Подобие профилей скоростей позволяет также предположить, что отношение характерных линейных размеров есть величина постоянная, т.е. l / b = const. Следовательно, можно записать, что 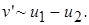 Поскольку
Поскольку 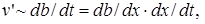 а
а 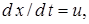 то закон нарастания толщины пограничного слоя по длине струи имеет следующий вид:
то закон нарастания толщины пограничного слоя по длине струи имеет следующий вид:
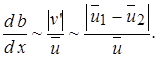 (10.23)
(10.23)
Величина 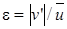 называется степенью турбулентности потока. Она всегда положительна, поэтому во всех случаях
называется степенью турбулентности потока. Она всегда положительна, поэтому во всех случаях 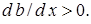
Характерное значение осредненной скорости 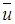 , фигурирующее в соотношении (10.23), определяется по формуле
, фигурирующее в соотношении (10.23), определяется по формуле
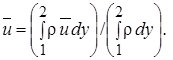 (10.24)
(10.24)
То обстоятельство, что усреднение скорости в этом уравнении осуществляется по толщине струи, а не по площади ее поперечного сечения, объясняется отмеченным ранее фактом практической независимости закона расширения струи от ее геометрии. В случае несжимаемого газа (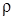 = const предполагается во всех дальнейших выкладках) для профиля скорости, описываемого уравнением Шлихтинга, среднемассовая скорость близка к среднеарифметической абсолютных значений скоростей
= const предполагается во всех дальнейших выкладках) для профиля скорости, описываемого уравнением Шлихтинга, среднемассовая скорость близка к среднеарифметической абсолютных значений скоростей
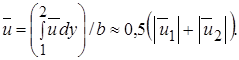 (10.25)
(10.25)
Используя это выражение, получаем следующий закон увеличения толщины пограничного слоя
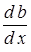 ~
~ 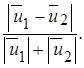 (10.26)
(10.26)
Таким образом, и при движущейся окружающей среде в пределах начального участка струи 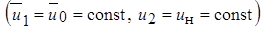 толщина пограничного слоя пропорциональна удалению от плоскости сопла
толщина пограничного слоя пропорциональна удалению от плоскости сопла 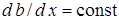 или b = const× х, где
или b = const× х, где 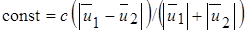 . Значение коэффициента с находится экспериментально.
. Значение коэффициента с находится экспериментально.
Учитывая, что для затопленной струи 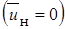 b 3 = c x, можно записать
b 3 = c x, можно записать
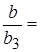
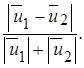 (10.27)
(10.27)
Нетрудно заметить, что отличие закономерностей расширения струи, развивающейся в спутном и встречном потоках, от закономерностей расширения затопленной струи определяется соотношением скоростей 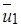 и
и 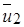 . При спутном движении двух струй (или струи и окружающей среды) скорости на границах пограничного слоя направлены одинаково, поэтому с увеличением
. При спутном движении двух струй (или струи и окружающей среды) скорости на границах пограничного слоя направлены одинаково, поэтому с увеличением 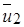 абсолютная величина разности (
абсолютная величина разности (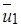 -
- 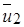 ) убывает, тогда для струи в спутном потоке имеем:
) убывает, тогда для струи в спутном потоке имеем:
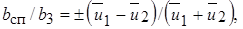 (10.28)
(10.28)
причем знак минус берется при 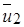 >
> 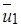 .
.
Из выражения (10.28) следует, что о турбулентной струе как таковой можно говорить лишь при 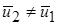 . При
. При 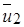 =
= 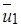
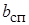 = 0. Физически это означает однородность потока уже в выходном сечении струи.
= 0. Физически это означает однородность потока уже в выходном сечении струи.
При распространении струи во встречном потоке скорости на границах пограничного слоя имеют противоположное направление, т. е. геометрическая разность скоростей равна сумме их абсолютных значений, поэтому 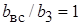 . Иными словами, при встречном движении струй (или струи и окружающей среды) расширение пограничного слоя не зависит от соотношения скоростей на его границах и подчиняется тому же закону, что и расширение затопленной струи. Этот несколько неожиданный результат объясняется тем обстоятельством, что вблизи границы раздела двух встречных потоков формируется область с нулевой скоростью движения, и вытекающая струя развивается при условиях, когда на ее границах эффективная скорость окружающей среды равна нулю.
. Иными словами, при встречном движении струй (или струи и окружающей среды) расширение пограничного слоя не зависит от соотношения скоростей на его границах и подчиняется тому же закону, что и расширение затопленной струи. Этот несколько неожиданный результат объясняется тем обстоятельством, что вблизи границы раздела двух встречных потоков формируется область с нулевой скоростью движения, и вытекающая струя развивается при условиях, когда на ее границах эффективная скорость окружающей среды равна нулю.
Начальный участок струи. В начальном участке струи, вытекающей в окружающую среду со скоростью 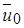 ,
, 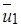 =
= 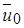 = const и
= const и 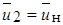 = const, поэтому здесь при спутном движении b = ± c x (1 - m)/(1 + m), где
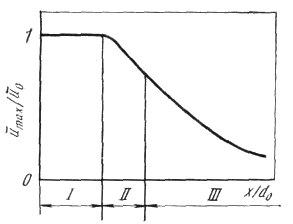
= const, поэтому здесь при спутном движении b = ± c x (1 - m)/(1 + m), где 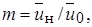 a опытный коэффициент c = 0,27 (рис. 10.4).
a опытный коэффициент c = 0,27 (рис. 10.4).
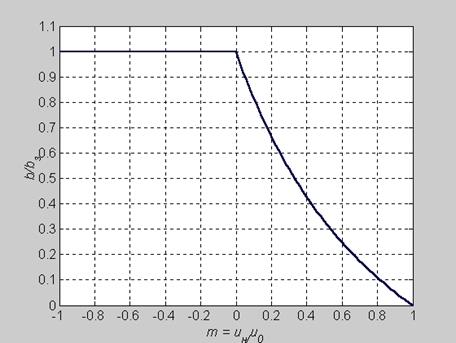
Рис. 10.4. Зависимость толщины пограничного слоя струи несжимаемой жидкости от скорости внешнего потока
Уравнение b = ± c x (1 - m)/(1 + m) определяет изменение вдоль начального участка толщины пограничного слоя b, расположенного между внешней границей у 2 и внутренней у 1, причем b = у 1 - у 2. Для установления вида функций у 1(x) и у 2(x) воспользуемся законами сохранения массы и количества движения газа. Согласно первому из них количество газа, протекающего через некоторое сечение пограничного слоя плоской струи 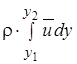 должно быть равно сумме расходов газа через границу
должно быть равно сумме расходов газа через границу 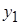
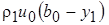 и через границу y 2
и через границу y 2 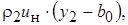 т.е.
т.е.
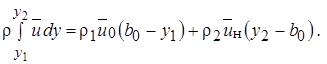 (10.29)
(10.29)
Аналогичным образом, количество движения газа в выделенном сечении складывается из количества движения газов, проходящих через границы 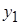 и
и 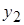 , т.е.
, т.е.
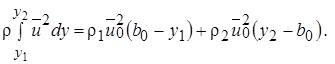 (10.30)
(10.30)
Умножив уравнение (10.29) на 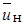 и вычитая почленно полученное выражение из соотношения (10.30), получим
и вычитая почленно полученное выражение из соотношения (10.30), получим
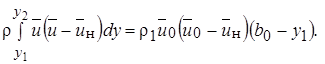
или при 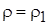
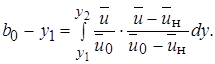 (10.31)
(10.31)
Используя уравнения (10.21) и (10.22), выражению (10.31) можно придать следующий вид:
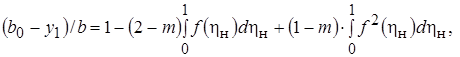
откуда после вычисления интегралов
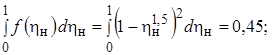
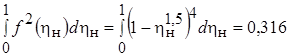
находим
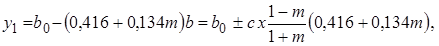 (10.32)
(10.32)
где знак плюс соответствует m>1
Следовательно,
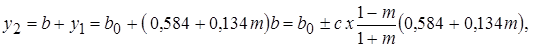 (10.33)
(10.33)
где знак минус соответствует m > 1.
Длину начального участка определим из условия 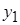 = 0, что эквивалентно достижению внутренней границей пограничного слоя оси струи:
= 0, что эквивалентно достижению внутренней границей пограничного слоя оси струи:
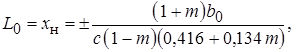 (10.34)
(10.34)
где знак минус отвечает режиму m > 1.Это выражение приблизительно справедливо и для осесимметричной струи; необходимо только 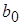 заменить на
заменить на 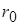 .
.
Для затопленной струи (m = 0) из этого уравнения получаем L з/ b 0 = 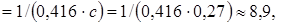 что хорошо соответствует экспериментальным данным.
что хорошо соответствует экспериментальным данным.
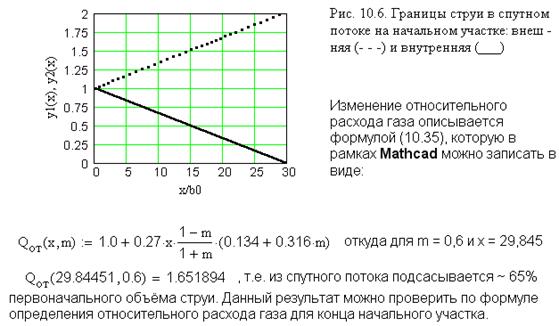
Расход газа, протекающего через половину плоской струи в ее начальном участке
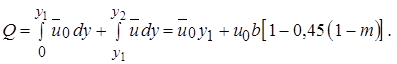
Учитывая, что 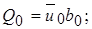 а также используя выражения для относительного расхода газа имеем
а также используя выражения для относительного расхода газа имеем
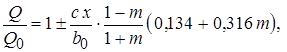 (10.35)
(10.35)
что дает для конца начального участка
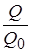 ½
½ 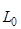 = 1 +
= 1 + 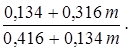
Для затопленной струи (m = 0), отсюда находим Q = Q 0/ L з = 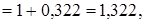 т.е. на начальном участке такая струя подсасывает из окружающей среды почти треть своего начального расхода. По мере увеличения m интенсивность подсоса возрастает, достигая при m >> 1 значения
т.е. на начальном участке такая струя подсасывает из окружающей среды почти треть своего начального расхода. По мере увеличения m интенсивность подсоса возрастает, достигая при m >> 1 значения 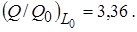
При использовании приведённых выше формул в практических расчётах необходимо учитывать следующие обстоятельства. Уравнения (10.32) ¸ (10.35) отражают формальные математические преобразования, которые не всегда соответствуют реальной физической ситуации. В самом деле, при m = 1 струи как таковой фактически не существует. В то же время, формула (10.34) даёт бесконечное значение длины начального участка. Далее, при m > 1 струя является обратной, т.е. подсос осуществляется спутным потоком из вдуваемой струи. Обратная струя закрывается, когда скорость на оси "струи" с заданной точностью совпадает со скоростью внешнего потока.
Основной участок струи. Более сложной задачей является определение очертаний основного участка струи в спутном потоке. В этом случае формула (10.28) приобретает вид:
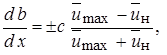 (10.36)
(10.36)
где 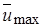 - скорость на оси основного участка струи (знак минус берется при
- скорость на оси основного участка струи (знак минус берется при 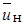 >
> 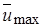 ). Константа c определяется опытным путем и для основного участка равна 0,22. Поскольку
). Константа c определяется опытным путем и для основного участка равна 0,22. Поскольку 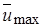 = f (x), является функцией расстояния граница струи в спутном потоке должна быть криволинейной, т.е d b / d x = var и для ее определения необходимо знать вид зависимости
= f (x), является функцией расстояния граница струи в спутном потоке должна быть криволинейной, т.е d b / d x = var и для ее определения необходимо знать вид зависимости 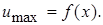
Для отыскания закономерностей изменения скорости по оси струи, а также для определения границ струи воспользуемся уравнением сохранения количества движения, которое для изобарической струи имеет следующий вид
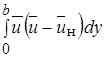 =
= 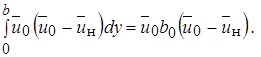 (10.37)
(10.37)
Это уравнение выводится способом, аналогичным рассмотренному ранее для начального участка.
Используя функцию Шлихтинга, вместо выражения (10.37) получаем:
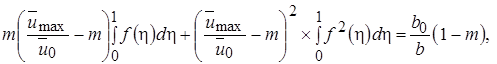
или, заменив интегралы их значениями,
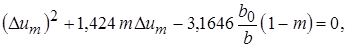 (10.38)
(10.38)
где 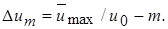
Решая квадратное уравнение (10.38), находим
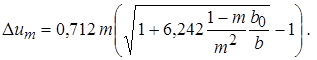
Для затопленной струи (m = 0), учитывая, что b = с х = 0,22 х, из уравнения (10.38) имеем 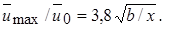
Запишем уравнение (10.36) в виде:
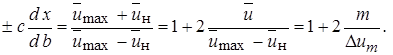
Подставив в это выражение значение 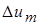 и интегрируя его, приходим к уравнению, связывающему толщину струи с продольной координатой х
и интегрируя его, приходим к уравнению, связывающему толщину струи с продольной координатой х
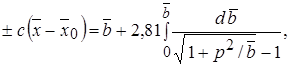 (10.39)
(10.39)
где 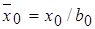 - безразмерное расстояние от начального сечения до полюса основного участка, в котором толщина струи равна нулю;
- безразмерное расстояние от начального сечения до полюса основного участка, в котором толщина струи равна нулю; 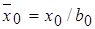 ;
; 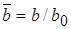 ;
; 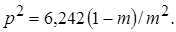 Выполняя интегрирование в правой части уравнения (10.39), для m < 1 получаем окончательно
Выполняя интегрирование в правой части уравнения (10.39), для m < 1 получаем окончательно
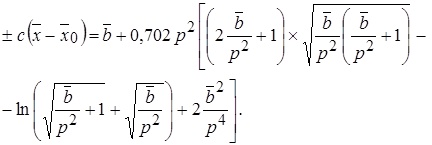 (10.40)
(10.40)
При практических расчетах для данного значения m вычисляют 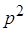 , а затем, изменяя безразмерную толщину струи b, находят по уравнению (10.40) соответствующую координату
, а затем, изменяя безразмерную толщину струи b, находят по уравнению (10.40) соответствующую координату 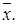 При этом положение полюса
При этом положение полюса 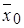 определяют по соотношению:
определяют по соотношению:
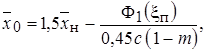 (10.41)
(10.41)
где
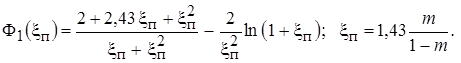
 По найденной зависимости
По найденной зависимости 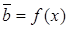 вычисляют изменение
вычисляют изменение 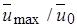 вдоль потока (рис. 10.5).
вдоль потока (рис. 10.5).
Рис. 10.5. Схема изменения осевой скорости по длине струи на начальном (I), переходном (II) и основном (III) участках
В случае, когда струя имеет меньшую скорость, чем окружающая среда (m > 1), уравнение (10.40) непригодно, так как при этом получаются мнимые значения величины 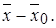 Для m > 1 целесообразно вести отсчет координаты от переходного сечения струи
Для m > 1 целесообразно вести отсчет координаты от переходного сечения струи 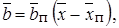 в котором избыточная скорость на оси приблизительно равна избыточной скорости истечения
в котором избыточная скорость на оси приблизительно равна избыточной скорости истечения 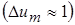 ; тогда вместо выражения (10.39) получаем уравнение
; тогда вместо выражения (10.39) получаем уравнение
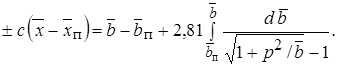
Поскольку изменяется нижний предел интегрирования, то окончательное выражение усложняется. Однако оно имеет ту же структуру, что и уравнение (10.40), поэтому здесь не приводится. Отметим только, что 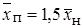 , а
, а 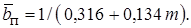
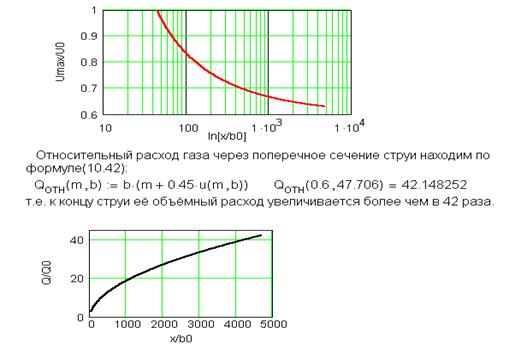
Наконец, приведем выражение, определяющее относительный расход газа через поперечное сечение струи в основном участке и справедливое при 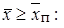
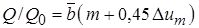 . (10.42)
. (10.42)
Аналогичным вышеописанному способом выполняется анализ более сложных случаев развития турбулентной струи в спутном потоке: осесимметричной струи, неизотермической струи и т.д. С конкретными решениями задач для этих случаев можно познакомиться по монографиям Г. Н. Абрамовича и другой литературе.
Пример 10.2. Оценить параметры струи несжимаемого газа, развивающегося в спутном потоке при соотношении скоростей m = 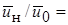 0.6. Построить контуры струи, а также график изменения скорости на оси струи по её длине.
0.6. Построить контуры струи, а также график изменения скорости на оси струи по её длине.
Для решения подобных задач весьма удобен пакет Mathcad, позволяющий легко выполнить многовариантные решения. Ниже представлена схема использования пакета.

Перейдём теперь к анализу закономерностей развития струи в основном участке. Здесь необходимые величины вычисляются в такой последовательности: xп, F1(xп), 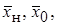 а затем выполняются расчёты по формуле (10.40).
а затем выполняются расчёты по формуле (10.40).
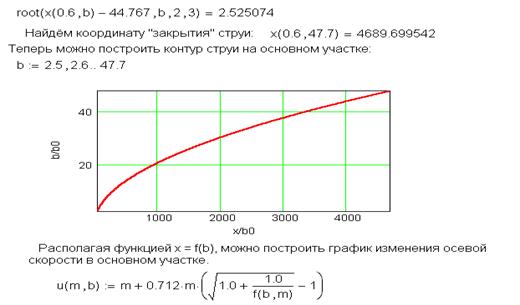
На этом этапе особенно проявляются преимущества пакета Mathcad, поскольку в его рамках можно строить не только графики зависимостей между отдельными функциями, но и обратные им.
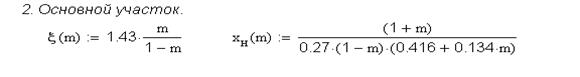

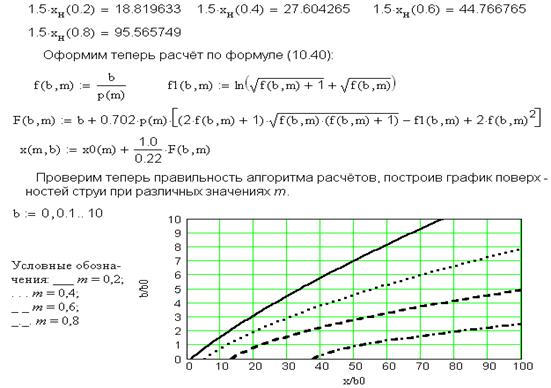
Можно видеть, что значение b / b 0 = 0 при значениях x / b 0 соответствующих координатам полюсов струи.
При развитии в спутном потоке длина струи определяется скоростью внешней среды, т.е. значением m. Очевидно, можно считать, что струя "закрылась", если относительная скорость на её оси u max/ u 0 будет равна (1,05 ¸ 1,10) m. Используя это определение, из уравнения для D um можно найти значение b / b 0, соответствующее концу струи,
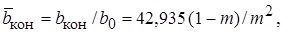
откуда для m = 0,6 получаем: 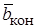 = 47,706. Из графика
= 47,706. Из графика 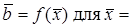 44,767 находим
44,767 находим 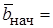 2,5. Можно также воспользоваться специальной командой Mathcad.
2,5. Можно также воспользоваться специальной командой Mathcad.
 2015-05-13
2015-05-13 2119
2119








