|
Рассмотрим передачу тепла стенки кругового цилиндра от нити, расположенной по оси цилиндра, через слой газа. Если нить нагревать электрическим током, то через некоторое время устанавливается стационарное состояние , при котором температуры 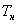 - нити и - нити и 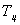 - цилиндра, неизменны; тогда от нити к цилиндру передается энергия W. - цилиндра, неизменны; тогда от нити к цилиндру передается энергия W.
Выберем такой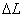 – участок длины нити, чтобы температура вдоль него была постоянной. При этом величина – участок длины нити, чтобы температура вдоль него была постоянной. При этом величина 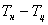 зависит oт W и теплопроводности газа. зависит oт W и теплопроводности газа.
Из уравнения теплопроводности, 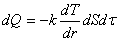 следует: следует:
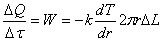 (1) (1)
где 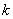 – коэффициент теплопроводности, – коэффициент теплопроводности,
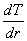 - градиент температуры, - градиент температуры,
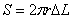 - площадь поверхности любого цилиндрического слоя длины DL (см. рис. 1) - площадь поверхности любого цилиндрического слоя длины DL (см. рис. 1)

рис.1
Найдем из уравнения (1)
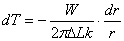
Интегрируя получим :
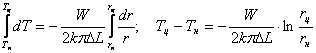
Измерив температуры 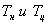 и зная геометрические размеры прибора и W, можно вычислить коэффициент теплопроводности: и зная геометрические размеры прибора и W, можно вычислить коэффициент теплопроводности:
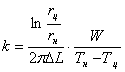 (2) (2)
Прибор состоит из длинного стеклянного цилиндра 1 (рис. 1).

рис.2
Вдоль цилиндра натянута 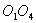 - тонкая платиновая нить, нагреваемая током от аккумуляторов 2. величину протекающего через нить тока можно регулировать магазином сопротивлений 3 и измерять амперметром 4. Падение напряжения на участке длины - тонкая платиновая нить, нагреваемая током от аккумуляторов 2. величину протекающего через нить тока можно регулировать магазином сопротивлений 3 и измерять амперметром 4. Падение напряжения на участке длины 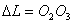 измеряется потенциометром 5. Ток замыкается ключом 6, температура стенки цилиндра измеряется термометром, 8 – клапан, 9 – зажим. Для уменьшения конвекции цилиндр расположен вертикально. измеряется потенциометром 5. Ток замыкается ключом 6, температура стенки цилиндра измеряется термометром, 8 – клапан, 9 – зажим. Для уменьшения конвекции цилиндр расположен вертикально.
Выполнение работы
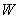 определяется по току и падению напряжения на участке нити длины DL. определяется по току и падению напряжения на участке нити длины DL.
 (3) (3)
где 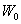 - мощность излучения. При сравнительно невысокой температуре - мощность излучения. При сравнительно невысокой температуре 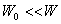 , поэтому величиной , поэтому величиной 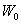 в формуле (З) можно пренебречь. Температура стенок цилиндра измеряется термометром. Температура нити вычисляется по её сопротивлению в формуле (З) можно пренебречь. Температура стенок цилиндра измеряется термометром. Температура нити вычисляется по её сопротивлению
 , , 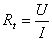
где 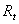 - сопротивление нити при температуре t°С, - сопротивление нити при температуре t°С,
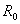 - сопротивление нити при 0°С, - сопротивление нити при 0°С,
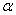 - термический коэффициент сопротивления. - термический коэффициент сопротивления.
Величины 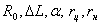 - постоянные прибора, они указаны на рабочем месте. - постоянные прибора, они указаны на рабочем месте.
Цилиндр присоединен к насосу и давление воздуха в нем можно изменять.
Давление воздуха в цилиндре измеряется манометрами. Сравнительно большие давления - U - образным ртутным манометром, а малые-компрессионным двух предельным манометром Мак-Леода.
Таким образом, k можно определять на интервале давлений от атмосферного до такого давления, при котором средняя длина свободного пробега молекул воздуха сравнима с линейными размерами цилиндра.
Последовательность операций
- Поставить рукоятку магазина сопротивлений так, чтобы его сопротивление было 99,9 Ома. Это необходимо для того, чтобы не испортить магазин сопротивлений и нить.
- Включить ключ и, вращая рукоятки магазина, установить ток накала нити равным 150 мА.
- Измерять потенциометром падение напряжения на
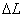 . .
- Закрыть клапан 8 и зажим 9 и включить насос.
- Приоткрыв клапан 8 на короткое время, немного уменьшить давление в системе и, закрыв клапан 8, измерить падение напряжения на DL, поддерживая величину тока накала равной 150 мА и соответствующее давление в системе.
Так измерять в интервале давлении до нескольких торр 5 или 6 раз.
6. Установить ток накала на 100 мА и измерять соответствующие падения напряжения и давления от нескольких торр до 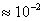 торр 10-12 раз. торр 10-12 раз.
Примечание. Малые давления измеряются манометром Мак-Леода при открытом клапане 8. Манометр Мак-Леода имеет два предела измерений для сравнительно больших и малых давлений. Его постоянные 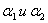 написаны на шкале. написаны на шкале.
При использовании более широкого капилляра пренебрегают наличием узкого.
Рекомендуемая таблица для записи измерений
Атмосферное
даление
Р= тор |
Постоянные Мак-Леода 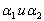
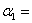 ; ; 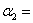 ; ; |
I ампер |
U
вольт |
R
ом |
W
ватт |
Показания
U-обр. манометра |
Показания
Мак-Леода |
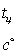
|
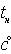
|
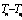
|
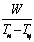
|
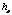
мм
|
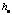
мм
|
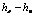
мм
|
р
тор |
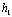
мм
|
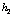
мм
|
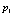
тор
|
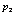
тор
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Построить зависимость 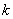 от давления. от давления.
|


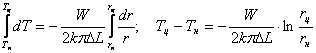
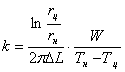 (2)
(2)









