Понятие математической модели

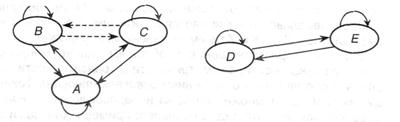
Обсудим частное определение модели, принятое в математике; в дальнейшем будем называть его математической моделью в узком значении термина:

Математическая модель - это множество элементов произвольной природы, на которых определено конечное множество отношений.

Будем обозначать М = {т₁, m₂…} - множество элементов (его называют несущим множеством ), R = {R₁, R₂ …R_n} - множество отношений между ними.

Определение, безусловно, нуждается в комментариях.

1. В математической модели не конкретизируется, каков характер (природа) элементов множества М - он может быть любым. Кроме того, отсутствует требование дискретности этого множества, т.е. в общем случае оно может содержать бесконечное количество элементов; примером может служить множество вещественных чисел, для которых определены отношения а > b или а₂ = b.

2. На одном и том же множестве могут быть построены различные модели, если будут выделены различные группы отношений. Например, учебную группу можно рассматривать как объединение субъектов с их межличностными отношениями, но можно выделить информационные отношения, имущественные, родственные и пр. Соответственно, будут строиться и описываться различные математические модели.

3. Характер отношений между элементами множества определяется свойствами, которыми элемент может обладать или, наоборот, не обладать. Например, для множества людей определено отношение «быть другом». Для каждого отдельного элемента (т.е. человека) существует большее или меньшее число элементов из того же множества, обладающие набором свойств (качеств), позволяющих установить указанное отношение; но имеются и те элементы, которые необходимым свойством не обладают, и данное отношение не устанавливается. Таким образом, отношения определяются атрибутами элементов множества: R_k = R_k(a₁ ... a_p). Важно, что число отношений и количество атрибутов конечны.

4. Отношения между элементами множества могут носить парный (бинарный) и непарный характер. Например, для элементов множества целых чисел определены парные отношения x_i = x_i-1 + 1, x_i = x_i+1 - 1. Они и множество целых чисел определяют одну из возможных математических моделей для данного множества. В качестве примера непарных отношений можно рассмотреть отношение а∙х + b = 0 для некоторых троек чисел а, b, х (при а ≠ 0) из множества рациональных чисел справедливо, следовательно, они также образуют математическую модель (в отличие от остальных троек, которые этому отношению не удовлетворяют и, таким образом, в данную модель не входят).

Для описания математических моделей используются языковые и графические средства. Язык описания может быть формализованным (например, язык математических формул) или естественным. Графическая форма, как всегда, обеспечивает удобство общего обзора модели, однако, наглядность эта проявляется только в случае бинарных отношений; если отношения в модели не являются бинарными, изображать модель в виде графа становится неудобно, и для их представления используются языковые средства.

Рассмотрим графическую форму модели, соответствующей следующему словесному описанию: «А учится в одной группе с В и С, но не с D и Е, которые учатся в другой группе». Здесь М = {А, В, С, D}, а отношением R будет «учиться в одной группе». Вершинами графа являются элементы несущего множества, а его дугами - отношения.

Отношения между элементами множества R_k могут обладать различными свойствами, но важнейшими из них являются три: рефлексивность, симметричность и транзитивность.

R обладает свойством рефлексивности,если любой элемент М, на котором R определено, вступает в отношение с самим собой.

Отношение «учиться в одной группе» обладает свойством рефлексивности, поскольку каждый студент учится сам с собой в одной группе. На графе свидетельством рефлексивности являются дуги, начинающиеся и заканчивающиеся на одном и том же элементе. Другим примером рефлексивного отношения является «равенство» (если а = b, очевидно, а = а). Примером нерефлексивных отношений могут служить «больше» (а > b) или «быть родителем» (очевидно, что ничто не порождает самое себя).

R обладает свойством симметричности,если из того, что элемент т, множества М связан этим отношением с элементом т₂, то обязательно и т₂ связан с т₁ тем отношением.

На графе симметричность отношения видна в том, что дуги, связывающие вершины, являются парными и противоположно направленными. Рассматриваемое в данном примере отношение симметрично, поскольку, если А учится с B в одной группе, то, очевидно, и B учится с A в одной группе. Примерами несимметричных отношений могут служить «быть начальником», «быть родителем», «больше». На графе несимметричное отношение изображается одинарной направленной дугой. Наконец,

Отношение R транзитивно, если из того, что этим отношением связаны т₁ и т₂, а также т₁ и т₃, следует, что между m₂ и m₃ имеется то же отношение.

Очевидно, рассматриваемое отношение транзитивно, что отражено парными пунктирными дугами, связывающими B и С. Примером нетранзитивного отношения является «быть родителем»: если справедливо, что X является родителем Y, а также X является родителем Z, то Y и Z таким отношением не связаны.

Если некоторое отношение R обладает одновременно свойствами рефлексивности, симметричности и транзитивности, то говорят, что оно является отношением эквивалентности. Такие отношения разбивают множество М на непересекающиеся классы эквивалентности - это видно из нашего примера: классами эквивалентности оказываются А, В, С и D, Е, поскольку они учатся в разных группах, но связаны одним типом отношений.

Помимо рассмотренных свойств отношений возможны противоположные им свойства - антирефлексивность, антисимметричность и нетранзитивность. Существование таких обратных свойств означает отсутствие прямого свойства в отношениях между любой парой элементов М.

Комбинацией свойств из приведенной шестерки (прямых и обратных) можно охарактеризовать различные отношения. Например, можно показать, что отношение «≤» является рефлексивным, транзитивным и антисимметричным; отношение «<» - транзитивным, антисимметричным и антирефлексивным.

Математические модели в узком значении термина широко применяется в теории принятия решений, математической лингвистике, представлении знаний и ряде других разделов информатики. Однако, как уже указывалось, чаще термин «математическая модель» используется в широкой трактовке как описание задачи с использованием формализма математики.

Модели проверяемые и непроверяемые

Характеристики канала связи

Пример 5.1

Классификация и примеры структур данных

Пример 3.1.

Вернуться в оглавление: Теоретические основы информатики