Пример 3.1.

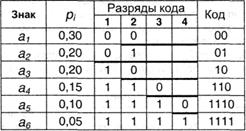
Пусть имеется следующая таблица префиксных кодов:

Требуется декодировать сообщение:

00100010000111010101110000110

Декодирование производится циклическим повторением следующих действий:

(a) отрезать от текущего сообщения крайний левый символ, присоединить справа к рабочему кодовому слову;

(b) сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (а);

(c) декодировать рабочее кодовое слово, очистить его;

(d) проверить, имеются ли еще знаки в сообщении; если «да», перейти к (а).

Применение данного алгоритма дает:

Доведя процедуру до конца, получим сообщение: «мама мыла раму».

Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных. Мы рассмотрим две схемы построения префиксных кодов.

Префиксный код Шеннона-Фано

Данный вариант кодирования был предложен в 1948-1949 гг. независимо Р. Фано и К. Шенноном и по этой причине назван по их именам. Рассмотрим схему на следующем примере: пусть имеется первичный алфавит А, состоящий из шести знаков а₁ ...а₆ с вероятностями появления в сообщении, соответственно, 0,3; 0,2; 0,2; 0,15; 0,1; 0,05. Расположим эти знаки в таблице в порядке убывания вероятностей (см. табл. 3.2). Разделим знаки на две группы таким образом, чтобы суммы вероятностей в каждой из них были бы приблизительно равными. В нашем примере в первую группу попадут a₁ и а₂ с суммой вероятностей 0,5 - им присвоим первый знак кода "0". Сумма вероятностей для остальных четырех знаков также 0,5; у них первый знак кода будет "1". Продолжим деление каждой из групп на подгруппы по этой же схеме, т.е. так, чтобы суммы вероятностей на каждом шаге в соседних подгруппах были бы возможно более близкими. В результате получаем:

Из процедуры построения кодов легко видеть, что они удовлетворяют условию Фано и, следовательно, код является префиксным. Средняя длина кода равна:

I₁^(A) = 2,390 бит. Подставляя указанные значения в (3.5), получаем избыточность кода Q(A,2) = 0,0249, т.е. около 2,5%. Однако, данный код нельзя считать оптимальным, поскольку вероятности появления 0 и 1 неодинаковы (0,35 и 0,65, соответственно). Применение изложенной схемы построения к русскому алфавиту дает избыточность кода 0,0147.

Префиксный код Хаффмана

Способ оптимального префиксного двоичного кодирования был предложен Д. Хаффманом. Построение кодов Хаффмана мы рассмотрим на том же примере. Создадим новый вспомогательный алфавит A₁, объединив два знака с наименьшими вероятностями (а₅ и а₆) и заменив их одним знаком (например, а⁽¹⁾); вероятность нового знака будет равна сумме вероятностей тех, что в него вошли, т.е. 0,15; остальные знаки исходного алфавита включим в новый без изменений; общее число знаков в новом алфавите, очевидно, будет на 1 меньше, чем в исходном. Аналогичным образом продолжим создавать новые алфавиты, пока в последнем не останется два знака; ясно, что количество таких шагов будет равно N - 2, где N - число знаков исходного алфавита (в нашем случае N = 6, следовательно, необходимо построить 4 вспомогательных алфавита). В промежуточных алфавитах каждый раз будем переупорядочивать знаки по убыванию вероятностей. Всю процедуру построения представим в виде таблицы:

Теперь в обратном направлении проведем процедуру кодирования. Двум знакам последнего алфавита присвоим коды 0 и 1 (которому какой - роли не играет; условимся, что верхний знак будет иметь код 0, а нижний - 1). В нашем примере знак а₁⁽⁴⁾ алфавита A⁽⁴⁾, имеющий вероятность 0,6, получит код 0, а a₂⁽⁴⁾ с вероятностью 0,4 - код 1. В алфавите А⁽³⁾ знак a₁⁽³⁾ получает от a₂⁽⁴⁾ его вероятность 0,4 и код (1); коды знаков a₂⁽³⁾ и a₃⁽³⁾, происходящие от знака a₁⁽⁴⁾ с вероятностью 0,6, будут уже двузначным: их первой цифрой станет код их «родителя» (т.е. 0), а вторая цифра - как условились - у верхнего 0, у нижнего - 1; таким образом, a₂⁽³⁾ будет иметь код 00, а a₃⁽³⁾ - код 01. Полностью процедура кодирования представлена в таблице, приведенной на с.70.

Из процедуры построения кодов вновь видно, что они удовлетворяют условию Фано и, следовательно, не требуют разделителя. Средняя длина кода, как и в предыдущем примере оказывается:

К(А,2) = 0,3 ∙ 2 + 0,2 ∙ 2 + 0,2 ∙ 2 +0,15 ∙ 3 + 0,1 ∙ 4 + 0,05 ∙ 4 = 2,45.

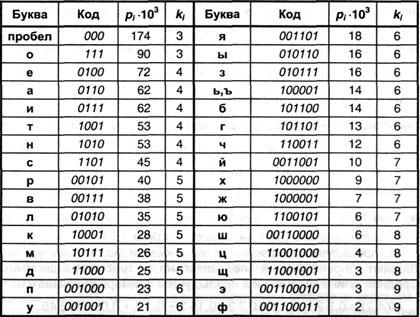
Избыточность снова оказывается равной Q(A, 2) = 0,0249, однако, вероятности 0 и 1 сблизились (0,47 и 0,53, соответственно). Более высокая эффективность кодов Хаффмана по сравнению с кодами Шеннона-Фано становится очевидной, если сравнить избыточности кодов для какого-либо естественного языка. Применение описанного метода для букв русского алфавита порождает коды, представленные в табл. 3.2. (для удобства сопоставления они приведены в формате табл. 3.1).

Таблица 3.2

Средняя длина кода оказывается равной К(r,2) = 4,395; избыточность кода Q(r,2) = 0,0090, т.е. не превышает 1 %, что заметно меньше избыточности кода Шеннона-Фано (см. выше).

Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана (см. [49, с.209-211]).

Таким образом, можно заключить, что существует способ построения оптимального неравномерного алфавитного кода. Не следует думать, что он представляет число теоретический интерес. Метод Хаффмана и его модификация - метод адаптивного кодирования (динамическое кодирование Хаффмана) - нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.

Классификация моделей

Пример 10.1

Связь компьютеров по телефонным линиям

Эквивалентные автоматы

Пример 4.2

Вернуться в оглавление: Теоретические основы информатики