 В движущейся жидкости связь между скоростями точек имеет сложный вид. Это связано с возможностью перемещения отдельных частиц относительно им подобных, что приводит к деформации выделенного объема жидкости – растяжению, т.е. изменению линейных размеров вдоль координатных осей, и изменению угла между гранями, образующими этот объем. Движение элементарного объема жидкости раскладывают на движение его как абсолютно твердого тела (квазитвердого тела) и деформационное движение.
В движущейся жидкости связь между скоростями точек имеет сложный вид. Это связано с возможностью перемещения отдельных частиц относительно им подобных, что приводит к деформации выделенного объема жидкости – растяжению, т.е. изменению линейных размеров вдоль координатных осей, и изменению угла между гранями, образующими этот объем. Движение элементарного объема жидкости раскладывают на движение его как абсолютно твердого тела (квазитвердого тела) и деформационное движение.
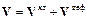 . (1.1)
. (1.1)
Уравнение (1.1) является математической формулировкой первой теоремы Гельмгольца.
Скорость любой точки квазитвердого тела определяется выражением
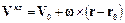 ,
,
где 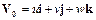 – вектор скорости точки тела, выбранной в качестве полюса;
– вектор скорости точки тела, выбранной в качестве полюса; 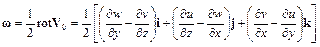 – вектор угловой скорости вращения рассматриваемой точки относительно полюса; r и r 0 – радиус-векторы, задающие положение точки и полюса в пространстве.
– вектор угловой скорости вращения рассматриваемой точки относительно полюса; r и r 0 – радиус-векторы, задающие положение точки и полюса в пространстве.
Скорость деформационного движения представляют в виде
 ,
,
где u, v и w – проекции вектора скорости полюса на оси координат; 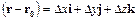 – радиус вектор точки относительно полюса.
– радиус вектор точки относительно полюса.
|
|
|
Матрицу, входящую в качестве сомножителя в правую часть уравнения, называют тензором скоростей деформаций
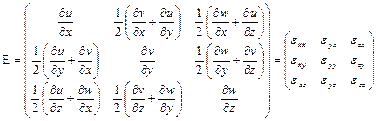 .(1.2)
.(1.2)
Используя введенные обозначения, скорость деформационного движения описывается следующим выражением
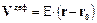 . (1.3)
. (1.3)
Величины, стоящие на главной диагонали матрицы и обозначенные одноименными индексами, представляют собой скорости относительных линейных деформаций вдоль соответствующих осей координат.
На рисунке изображен отрезок, связывающий две точки жидкости, движущиеся вдоль оси x в различные моменты времени. Абсолютное приращение длины отрезка за время dt вследствие различных значений скоростей его крайних точек
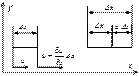
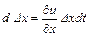 .
.
Скорость удлинения отрезка (скорость линейной деформации) равна
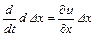 ,
,
а скорость увеличения длины относительно первоначальной (скорость относительной линейной деформации) определяется выражением
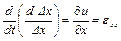 .
.
Величины, расположенные выше и ниже главной диагонали матрицы (1.2) и обозначенные разноименными индексами, представляют собой угловые скорости деформации граней выделенного объема в различных координатных плоскостях.
На рис. 1.1 представлена схема, поясняющая угловую деформацию жидкой частицы в процессе движения.
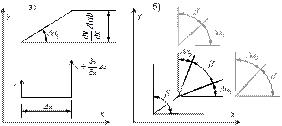
Рис. 1.1. Схема угловой деформации движущейся частицы жидкости
а) – поворот отрезка; б) – изменение угла между гранями
При движении отрезка Dx вдоль оси y (рис. 1.1, а) вследствие различия скоростей его концов происходит поворот на угол Da 1
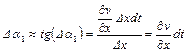 .
.
Угловая скорость этого поворота равна
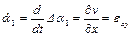 .
.
Угловая скорость поворота отрезка, параллельного в начальный момент оси y, равна
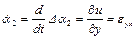 .
.
Возможность поворота всех граней элементарного объема жидкости приводит к изменению углов между соседними гранями в процессе движения 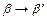 .
.
|
|
|
Одно и тоже изменение угла b между гранями может быть достигнуто различными сочетаниями поворотов граней (например, как показано на рис. 1.1, б, основным и тусклым цветами). Это приводит к неоднозначности в определении истинных значений угловых скоростей поворота граней, дающих одинаковый результат. В гидравлике условно принимают угловые скорости поворота каждой из соседних граней одинаковыми, равными среднему арифметическому значению угловых скоростей обоих граней
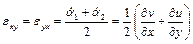 .
.
 2015-06-04
2015-06-04 438
438








