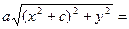Извлекая корень из обеих частей этого равенства, получим

± (а³—сх) (13)

Заметим теперь, что в силу равенства (12) должно быть |х| ≤ а. Так как 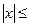а и с < а, то 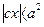, то число а² — сх положительно. Поэтому в правой части равенства (13) необходимо взять знак плюс. Так мы приходим к равенству (7), после чего получим равенство (6); последнее мы напишем в виде

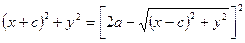
Отсюда

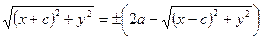(14)

Исследуем величину

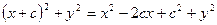
(15)

В силу равенства (12) имеем 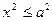. Далее 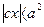, следовательно, число— 2сх по абсолютному значению меньше 2а². Наконец, также из равенства (12) заключаем, что 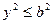, т.е. 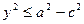или 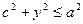. Ввиду этих обстоятельств, вся сумма в правой части (15) меньше 4а², значит, корень из этой суммы меньше 2а. Поэтому величина, стоящая внутри скобок в правой части (14), положительна, следовательно, в равенстве (14) перед скобками нужно брать знак плюс. Таким образом, мы получаем:

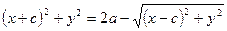
откуда сразу следует равенство (5).

Итак, уравнение (5) выводится из уравнения (12), как и уравнение (12) выводится из уравнения (5). Тем самым доказано, что уравнение (12) есть уравнение данного эл­липса, поскольку оно эквивалентно уравнению (5).

Уравнение (12) называется каноническим уравнением эллипса. Уравнение

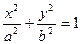
определяющее эллипс в некоторой системе декартовых прямо­угольных координат, есть уравнение второй степени; таким образом, эллипс есть линия второго порядка.