Нормальная форма уравнений состояния одномерной системы

Пусть динамика одномерной системы, имеющей один вход и один выход, описывается дифференциальным уравнением

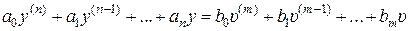, (8.16)

где , .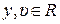

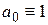Требуется найти уравнения состояния (8.3) в нормальной форме, эквивалентные уравнению (8.16).

Задача легко решается для частного случая (8.16), если m = 0, т.е. правая часть (8.16) будет иметь вид 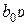. в (8.16) сделаем замену переменных 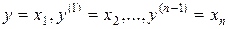. Дифференцируя последовательно каждое равенство, получим

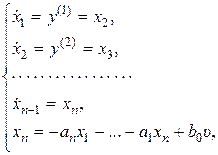
где последнее соотношение соответствует уравнению (8.16). Полученную систему с учетом 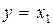запишем в виде уравнений состояния в нормальной форме:

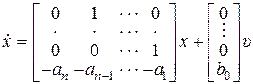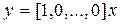, , (8.17)

где, как обычно, .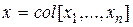

Если в (8.16) m > 0, то также можно получить уравнения состояния в нормальной форме. Вывести их несколько сложнее, поэтому дадим конечный результат. Для удобства будем в (8.16) полагать m = n. Очевидно, если m < n, то ряд первых коэффициентов 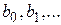будет равен нулю. Уравнения состояния в этом случае будут иметь следующий вид:

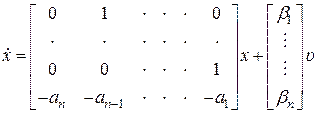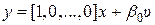, . (8.18)

Коэффициенты 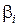определяются из решения системы линейных алгебраических уравнений, записанных в векторно-матричной форме:

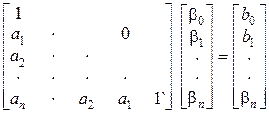. (8.19)

Из (8.19) следует, что 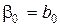, , 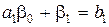,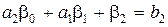…, откуда последовательно находятся , ,….

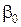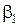Для физически реализуемых систем 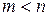и .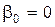

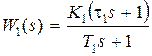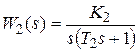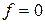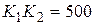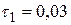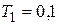Пример 8.5. Рассмотрим замкнутую систему управления стандартной структуры (см. рис. 3.1), где будем полагать , , , , с, 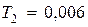с, с.

Передаточная функция разомкнутой системы будет равна

.

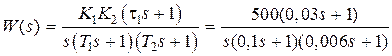Найдем дифференциальное уравнение разомкнутой системы, связывающее y и e: .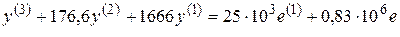

Коэффициенты этого уравнения , , , , , , .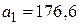

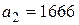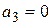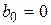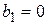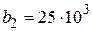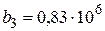Уравнение для определения 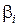имеет вид

,

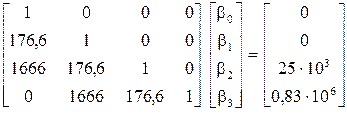откуда , , , .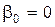

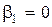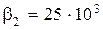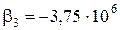Итак, уравнения состояния разомкнутой системы в нормальной форме имеют вид

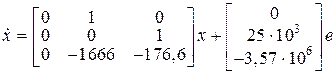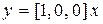, . (8.20)

Для получения уравнений состояния замкнутой системы учтем уравнение замыкания 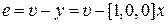, после подстановки которого в (8.20)
получим

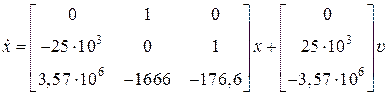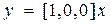, . (8.21)

Уравнения состояния замкнутой системы (8.21) уже не являются уравнениями в нормальной форме.