Теорема существования и единственности для дифференциального уравнения 1 – го порядка

Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:

P(x;y)dx + Q(x;y)dy = 0, (3)

где Р(х;у) и Q(x;y) — известные функции. Уравнение (3) удобно тем, что переменные х и у в нем равноправны, т. е. любую из них мож­но рассматривать как функцию другой. Отметим, что от одного вида записи ДУ можно перейти к другому.

Интегрирование ДУ в общем случае приводит к бесконечному мно­жеству решений (отличающихся друг от друга постоянными величи­нами). Легко догадаться, что решением уравнения у' = 2х является функция у = х², а также
у = х² + 1, у = х² – ln2и вообще у = х² + с, где с = const.

Чтобы решение ДУ приобрело конкретный смысл, его надо подчи­нить некоторым дополнительным условиям.

Условие, что при х = х_о функция у должна быть равна заданному числу y_о, т.е. у = y_о называется начальным условием. Начальное условие записывается в виде

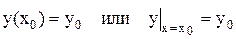. (4)

Теорема Коши (существования и единственности решения для ДУ 1 порядка). Если в уравнении (2) функция f(x; y) и ее частная про­изводная f¢_y(x;y) непрерывны в некоторой области D, содержащей точку (х_о;у_о), то существует единственное решение у = j(х) этого уравнения, удовлетворяющее начальному условию (4).

(Без доказательства).

Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку (х_о;у_о).

Итак, теорема Коши определяет существование единственного решения дифференциального уравнения первого порядка.