Квантовомеханическое рассмотрение импульсного ЯМР

2.1. Уравнение движения

Взаимодействие спина с магнитным полем описывается оператором энергии, гамильтонианом 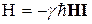, где I – оператор спина. Исходя из уравнения Шредингера, можно получить уравнение движения любой наблюдаемой (в том числе и магнитного момента). Положим, что волновые функции Y и F удовлетворяют уравнению Шредингера:

, .

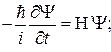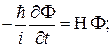Тогда для всякого оператора 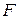можно записать уравнение

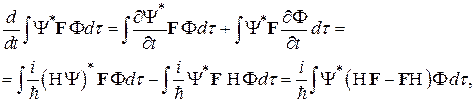
или , поскольку это верно для любых матричных элементов 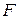. При выводе использовалось соотношение 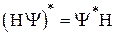, справедливое для эрмитовых операторов.

Нетрудно убедиться, что полученное уравнение эквивалентно классическому, если в качестве оператора выбрать ядерный спин, а гамильтониан описывает зеемановское взаимодействие:

, .

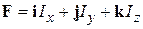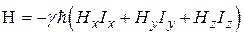2.2. Статистический ансамбль невзаимодействующих спинов.

Можно ли с помощью волновой функции одного спина описать ансамбль, состоящий из 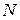одинаковых невзаимодействующих спинов в магнитном поле? Попытаемся это проделать, полагая, что спин равен 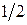. Запишем волновую функцию в виде суперпозиции “чистых” волновых функций: 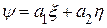, , 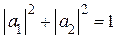причем 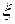соответствует спину, направленному вдоль поля, а 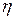– наоборот. Тогда компоненты макроскопической намагниченности ансамбля определяются следующими выражениями:

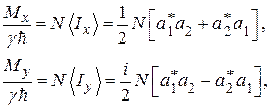
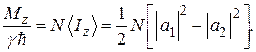
Последнее равенство кажется очевидным, если считать, что 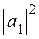и 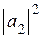есть относительные населённости уровней. Однако из первых двух следует, что поперечная намагниченность равна нулю, только ес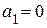ли или 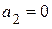, то есть в случае полной поляризации спинов, что не соответствует действительности. Итак, предположение о том, что для описания ансамбля спинов достаточно знать одночастичную волновую функцию оказалось несостоятельным. Для определения поперечной намагниченности следовало учитывать средние по ансамблю произведения коэффициентов: . Для наиболее полного описания системы спинов, в том числе и при наличии взаимодействия, требуется знание всех таких произведений. Последние являются элементами матрицы плотности 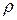. Полное количество состояний системы спинов равно , следовательно, размер матрицы плотности – 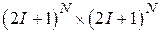, а её элементы равны .

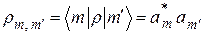Если известна матрица плотности, то можно определить среднее значение всякой наблюдаемой: 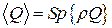. Зависимость матрицы плотности от времени описывается уравнением

.

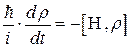В случае, если гамильтониан не зависит от времени, решением уравнения является

.

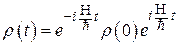Наиболее просто записывается равновесная матрица плотности в собственном представлении гамильтониана 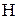. Если значения энергии обозначить 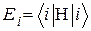, то недиагональные элементы матрицы плотности равны нулю, а диагональные 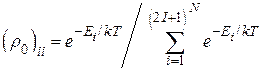равны заселённостям уровней энергии в соответствии со статистикой Больцмана.

2.3. Спад спиновой индукции и спиновое эхо

Формализм матрицы плотности позволяет объяснить явления спиновой индукции и спинового эхо. Запишем равновесную матрицу плотности для системы из 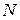спинов 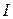: 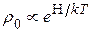, где 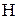– основной гамильтониан, описывающий взаимодействие спинов с магнитным полем, 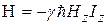, 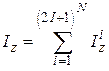. В высокотемпературном приближении (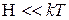) можно разложить матрицу плотности в ряд и ограничиться первым членом разложения 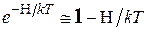, где 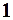– единичная матрица (оператор). Пренебрегая последней, окончательно запишем .

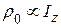Воздействие на матрицу плотности переменного магнитного поля, а также её эволюция описываются с помощью экспоненциальных операторов. Можно показать, что оператор 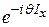поворачивает спиновые операторы на угол 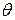вокруг оси 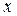, т.е. после воздействия 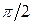-импульса .

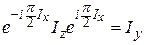В том случае, если распад поперечной намагниченности происходит благодаря диполь-дипольному взаимодействию ядерных спинов, дальнейшая эволюция матрицы плотности происходит по следующему закону:

,

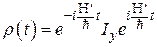где 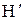– секулярная часть диполь-дипольного взаимодействия. (О причинах усечения гамильтониана дипольного взаимодействия см. описание лабораторной работы “Стационарный ЯМР в твердом теле”.) Таким образом, поперечная намагниченность будет зависеть от времени как

.

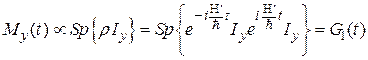Отметим, что последнее выражение записано в ВСК, вращающейся с частотой 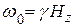, и описывает спад спиновой индукции (ССИ) – сигнал импульсного

ЯМР, связанный со стационарным сигналом 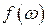фурье-преобразованием:

.

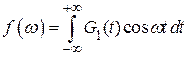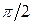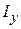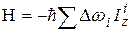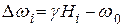В том случае, когда причиной уширения линии ЯМР является неоднородность магнитного поля, можно продемонстрировать механизм возникновения спинового эхо. Матрица плотности после -импульса также равна . Гамильтониан зеемановского взаимодействия спинов во вращающейся системе координат можно записать как , где , а 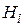– магнитное поле в месте расположения 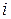-го спина. Тогда, в момент времени ,

.

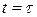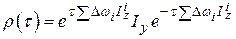Если в этот момент времени подать 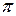-импульс, то после него

.

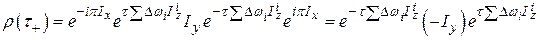Дальнейшее изменение матрицы плотности происходит как

.

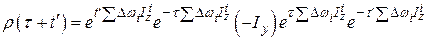Ясно, что когда 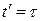(в момент времени 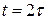), 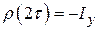. Это означает, что поперечная намагниченность восстановилась, но изменила знак, как это следует и из классической модели.