Игра в смешанных стратегиях

Пример 5. Исследовать платежную матрицу на наличие седловой точки и найти цену игры

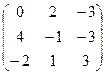
Решение. Используя рассмотренный выше алгоритм, получаем

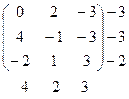
Отсюда находим

a=-2, b=2

Итак, нижняя и верхняя цены игры не совпадают. Оптимальными являются стратегии А₃ и В₂.

Ясно, что пока игроки придерживаются этих стратегий, средний выигрыш будет между числами -2 и 2. Однако, если игроку В станет известно, что игрок А выбрал стратегию А₃, то он немедленно ответит стратегией В₁ и сведет его выигрыш к -2. В свою очередь, на стратегию В₁ у игрока А имеется ответная стратегия А₂, дающая ему выигрыш 4. Таким образом, ситуацию А₃, В₂ нельзя признать равновесной.

Если матричная игра не имеет седловой точки, то применение минимаксных стратегий приводит к тому, что для каждого из игроков выигрыш не превышает а, а проигрыш не меньше b.

Можно ли увеличить выигрыш или уменьшить проигрыш? Решение находят в смешанных стратегиях.

Смешанной стратегией называется случайная величина, значениями которой являются чистые стратегии с соответствующими им вероятностями. Смешанную стратегию игрока А удобно записывать в виде следующей подстановки:

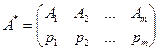
где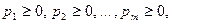

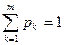
Аналогично, смешанную стратегию игрока В также удобно записывать в виде следующей подстановки

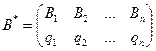
где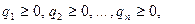

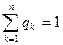
Очевидно, что каждая чистая стратегия является частным случаем смешанной стратегии. А именно, чистой стратегии А₁ соответствует подстановка

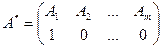
а чистой стратегии В₂ - подстановка

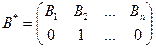
В общем случае чистой стратегии А_i соответствует следующий набор вероятностей:

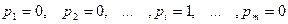
а чистой стратегии B_j - набор вероятностей

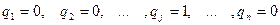
Будем считать, что для соблюдения секретности каждый из игроков применяет свои стратегии независимо друг от друга.

Итак, смешанные стратегии игроков А и В могут быть охарактеризованы заданием векторов вероятностей применения соответствующих стратегий:

P={p₁, p₂, …,p_m}

Q={q₁, q₂, …,q_n}

Следовательно, выбор игроком А стратегии А_i, а игроком В стратегии B_j, является случайным событием с вероятностью p_iq_j (по теореме умножения независимых событий). Тогда математическое ожидание выигрыша будет равно

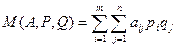
Число M(A,P,Q) будем считать средним выигрышем игрока А в условиях смешанных стратегий.

Стратегии А^* и В^*

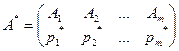
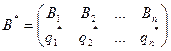
называются оптимальными, если

M(A,P,Q^*)≤M(A,P^*,Q^*)≤M(A,P^*,Q) (1)

Выигрыш, соответствующий оптимальному решению, называется ценой игры:

v=M(A,P^*,Q^*)

Цена игры удовлетворяет неравенству:

a≤v≤b

Решением матричной игры в смешанных стратегиях называется набор (P^*,Q^*,v), состоящий из оптимальных смешанных стратегий игроков и цены игры.

Использование в игре оптимальных смешанных стратегий обеспечивает первому игроку выигрыш, не меньший, чем при использовании им любой другой стратегии, а второму игроку – проигрыш, не больший, чем при использовании им любой другой стратегии.

Отметим два важных вопроса. Первый из них: какие матричные игры имеют решение в смешанных стратегиях? Имеет место основная теорема теории матричных игр, а именно,

Теорема Неймана. Для матричной игры с любой платежной матрицей существуют и равны между собой следующие величины:

,

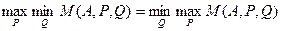причем существует хотя бы одна ситуация в смешанных стратегиях {P^*,Q^*), для которой выполняется равенство

M(A,P^*,Q^*)=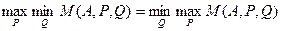

Второй вопрос: как находить решение матричной игры?

Пусть

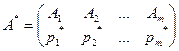
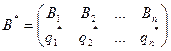
оптимальные смешанные стратегии и v – цена игры. Оптимальная смешанная стратегия игрока А состоит только из тех чистых стратегий A_i, (i=1,2,…,m), для которых

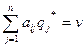(2)

Аналогично, оптимальная смешанная стратегия игрока В состоит только из тех чистых стратегий В_j, (j=1,2,…,n), для которых

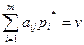(3)

Отсюда следует, что только те вероятности p_i могут быть отличны от нуля, для которых имеет место равенство (2), и только те вероятности q_j, для которых имеет место равенство (3). В связи с этим, если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то назовем ее активной стратегией.

Итак, если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

Это утверждение имеет большое практическое значение, так как указывает методы нахождения оптимальных стратегий при отсутствии седловой точки. Вот эти равенства:

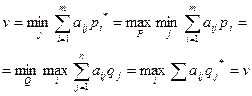
Простейшим случаем матричной игры является игра размера 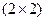. Если такая игра имеет седловую точку, то оптимальным решением является пара соответствующих чистых стратегий. Если игра не имеет седловой точки, то в соответствии с теоремой Неймана оптимальное решение существует и определяется парой смешанных стратегий

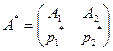
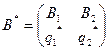
Найдем оптимальное решение этой игры. Для этого воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии А^*, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией ни пользовался игрок В.

В игре 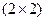любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А – это случайная величина, математическое ожидание которой равно цене игры v. Следовательно, средний выигрыш игрока А будет равен v для любой стратегии игрока В.

В соответствии с определением средний выигрыш игрока А, если он использует оптимальную смешанную стратегию

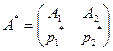
а игрок В - чистую стратегию В₁, равен цене игры, т.е.

a₁₁p₁^*+a₂₁p₂^*=v

Такой же средний выигрыш получает игрок А, если игрок В применяет стратегию В₂. Значит,

a₁₂p₁^*+a₂₂p₂^*=v

Учитывая, что p₁^*+p₂^*=1, получаем систему уравнений для определения оптимальной стратегии А^* и цены игры:

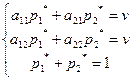
Решая эту систему, получаем вероятности оптимальной смешанной стратегии первого игрока

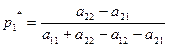
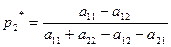(4)

и цену игры

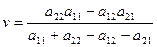(5)

По аналогии, учитывая, что q₁^*+q₂^*=1, получаем систему уравнений для определения оптимальной стратегии B^* и цены игры:

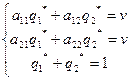
Решая эту систему, получаем вероятности оптимальной смешанной стратегии второго игрока

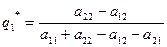
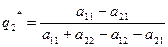(6)

При любой чистой стратегии игрока А средний проигрыш игрока В равен v.

Пример 6. Найти оптимальные стратегии игры с платежной матрицей

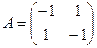
Решение. Очевидно, что седловая точка отсутствует, так как a=-1, b=1. Значит, решение надо искать в смешанных стратегиях. Как и ранее, средний выигрыш первого игрока или средний проигрыш второго обозначим через v. Системы уравнений (4), (5) в этом случае имеют вид:

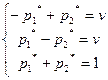
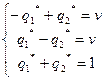
Решая эти системы, получаем:

p₁^*=p₂^*=0,5, q₁^*=q₂^*=0,5, v=0

Это значит, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом с вероятностью 0,5, при этом средний выигрыш равен 0.