2015-06-28
1005
Если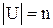 
, то булева алгебра (B 
, 
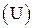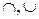
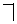) изоморфна булевой алгебре 
.
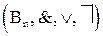Доказательство:
Итак, вспомним взаимно однозначное соответствие между B 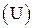и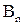 
.
Множеству М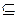 
B 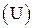соответствует 
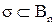, т.е.
. (*)
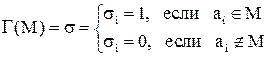Остается показать, что Г – изоморфизм, т.е. проверить выполнение равенства гомоморфизма алгебр для всех трех операций:
,
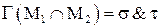
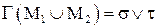
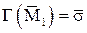если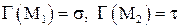 
.
Справедливость их вытекает из (*). Докажем, например второе:
- если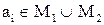 
, то i-ый разряд вектора 
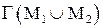равен 1;
но, с другой стороны, это означает, что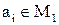 
или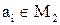 
, но это (по гомоморфизму) означает, 
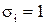или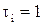 
, и, следовательно, i-ый разряд вектора 
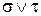равен 1;
- если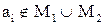 
, то i-ый разряд вектора 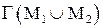равен 0;
но это означает, что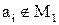 
и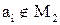 
, но это (по Г) означает, 
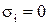и 
, и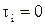, следовательно, i-ый разряд вектора 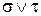равен 0.
Аналогично доказываются остальные равенства.
Эта теорема позволяет заменить теоретико-множественные операции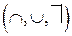 
над системой подмножеств поразрядными логическими операциями над двоичными векторами. Такая замена часто используется при программировании, поскольку представление двоичных векторов и поразрядные операции над ними реализуются очень просто.
Рассмотрим теперь множество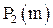 
всех логических функций m переменных 
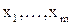. Оно замкнуто относительно операций 
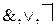(результат их применения к функциям из 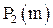снова дает функцию из 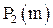, и, следовательно, образует конечную булеву алгебру 
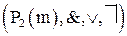, являющуюся подалгеброй булевой алгебры логических функций.
