Погрешности квадратурных формул

Погрешности квадратурных формул, рассмотренных в п.3, устанавливаются похожим образом. А именно, в каждом случае определяются локальные погрешности, которые затем суммируются.

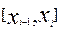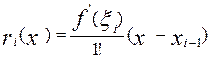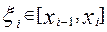
Рассмотрим формулу левых прямоугольников (8). Согласно формуле Тейлора погрешность интерполяционной формулы на отрезке составляет ,где . Тогда погрешность интегрирования формулы вида (4) описывается выражением

,

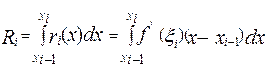которое, согласно обобщенной теоремы о среднем значении, можно представить в более удобной для последующего использования форме

,

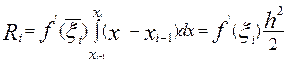где .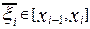

Тогда погрешность R формулы (8) равна

.

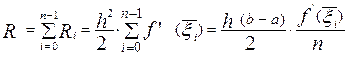Далее, предположим функцию f(x) непрерывно дифференцируемой на отрезке [a, b]. Тогда по теореме Вейерштрасса найдется значение 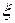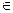[ a, b ] и выражение для описания погрешности принимает окончательный вид

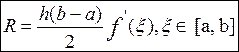. (12)

Используя (12), можно выбрать шаг h и число n, обеспечивающих заданную точность интегрирования 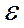. Действительно, пусть 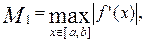, тогда

.

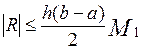Потребовав

,

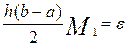получим

.

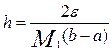Рассмотрим формулу трапеций (9).

Определим локальную погрешность интегрирования на отрезке [xi-1, xi]. Погрешность интерполяции равна

,

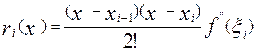где 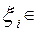[xi-1, xi]

Тогда, согласно теореме о среднем значении

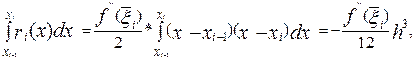
где 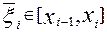. Далее, проводя суммирование локальных погрешностей, получим глобальную, допускаемую на отрезке [ a, b ] при использовании формулы трапеции

,

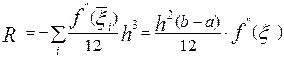где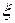

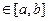
Проведем без доказательства погрешности

для правила Симпсона,–

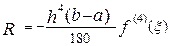
и для правила 3/8, -

.

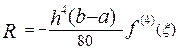Их обоснование см. в монографии: Крылов В.И., Бобков, Монастырный. Вычислительные методы. т2. –М.: Наука, 1977. -400с.

В заключении обратим внимание на следующий любопытный факт. Несмотря на более высокую степень интерполяционного многочлена, используемого в правиле 3/8, его итоговая погрешность интегрирования, при прочих равных условиях, выше, чем в правиле Симпсона.