Бинарные отношения

Для бинарных отношений можно определить дополнительные операции, отличающиеся от теоретико-множественных.

Пусть RÍ A ‰ В есть отношение из А в В. Обратное отношение R^-1 из В в А определяется следующим образом: упорядоченная пара

< b,a > 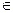R^-1Í B ‰ A Û < a,b >ÎRÍ A ‰ В.

Пример: R^-1={<x, a>, <y,a>, <y,b>, <x,c>}

c	●	○
d	○	●
a	●	●
	x	y

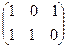
Композицие й двух отношений R₁(A,B) и R₂(B,C) называется отношение R(A,C)=R₁•R₂, состоящее из всех пар < а, с >ÎRÍA‰C, таких что существует хотя бы один элемент b 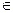B, такой что < a, b > Î R₁ и < b, c > ÎR₂:

R₁•R₂ƒ {< a, c >|$ b 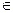B (< a, b > Î R₁)&(< b, c > Î R₂)}

Композиция отношений на множестве А снова является отношением на множестве А, то же справедливо для обратных отношений. Следовательно, в этом случае можно определить степени отношения R², R³, R⁴и т.д. А если ещё принять операцию объединения отношений как сумму, то можно рассматривать многочлены и даже функции.

NB. При матричном задании отношений композиция отношений представляется произведением матриц. Произведение вычисляется по правилам логического сложения и умножения.

Пример: R◦R^-1 = {< a,a>, <a,c>,<a,b>,<b,b>,<b,a>,<c,a>,<c,c> };

R^-1◦R = {< x,x>,<x,y>,<y,x>,<y,y>} – это полное отношение на Х.

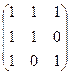
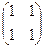
Пусть М – множество всех когда-либо живших мужчин. R – отношение на М² «быть сыном». Тогда R² – отношение «быть внуком», R^-1 – отношение «быть отцом».

Вопрос: что такое сумма (обратных) степеней?

Отношение R•R^-1 – называемое ядром – не является полным: это множество мужчин, не имеющих сыновей.

R^-1•R – тоже отношение на М – подмножества М, состоящие из братьев по отцу.

NB: последнее отношение разделило множество М на непересекающиеся подмножества, т.е. оказалось разбиением.

Дадим несколько определений, связанных с отношениями.

1. Образом элемента а 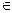А называется подмножество В:

im_R ( a ) = { b |< a,b >ÎR}

2. Областью значений отношения R называется подмножество В:

Im R=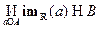

3. Прообразом элемента b 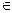B называется подмножество А:

coim_R(b) ={ a | < a, b >Î R }

4. Областью определения отношения R называется подмножество А:

Dom R=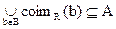

Если область определения отношения R совпадает с А, то отношение называется всюду определённым; в противном случае - частичным

5. Ядромотношения R из А в В называется отношение на А: R•R^-1

6. Сечением отношения R по множеству С 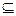А называется множество

{ y | < x, y >ÎR, x Î C} Í ImR

NB: при переходе к обратному отношению R→R^-1 определения, очевидно, меняются местами: Im R=Dom R^-1, Dom R=Im R^-1.

Пусть задано некоторое множество M, | M |=n. Рассмотрим отношение Р из булеана 2^М в множество целых чисел О={0,1,2,…,n}:

P={<x,k>|x 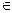M&k 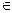O, |x|=k}.

Тогда ядром отношения Р будет отношение равномощности: отношение непусто только на подмножествах, имеющих равное число элементов. При этом на классах таких подмножеств отношение полное. Опять мы убеждаемся в том, что ядро отношения осуществляет разбиение множества (булеана), на котором оно определено, на непересекающиеся классы. Внутри классов отношение полное.