Пусть задано частично упорядоченное множество М. Отношение порядка в дальнейшем будем обозначать знаком 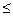 , двойственное к нему – знаком
, двойственное к нему – знаком 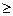 . Применим введённые в предыдущем разделе определения к подмножествам М, состоящим всего из двух элементов (!).
. Применим введённые в предыдущем разделе определения к подмножествам М, состоящим всего из двух элементов (!).
Пусть М – частично упорядоченное множество с частичным порядком ≤. Элемент х Î М называется нижней границей элементов a и b, если x ≤ b & x ≤ a.
Элемент v называется нижней гранью, если для любой границы x, x ≤ v.
Аналогично определяются верхняя граница y: a ≤ y & b≤y и верхняя граньu: u ≤y для любой границы y.
Обозначают нижние и верхние грани символами min(a,b) = inf(a,b) = aÙb и max(a,b) = sup(a,b) = aÚb соответственно.
Теорема. Если существует нижняя (верхняя) грань, то она единственна.
□ Пусть x = inf(a,b) & y = inf(a,b) → x ≤ y & y ≤ x → x = y. ■
Следствие. Каждая из граней представляет собой функцию Ù,Ú: М2 # М, т.е. является бинарной операцией на М.
Свойства граней/операций:
1.. aÙа = а, aÚа=а;
2. aÙb = bÙa; aÚb = bÚa.
3. (aΛb)Ùc = aÙ(bÙc); (aÚb)Úc = aÚ(bÚc).
Действительно, определение границ не зависит от порядка элементов, равно как и inf(inf(a,b),c) = inf(a, inf(c,b)).
Если вдобавок к этим свойствам грани обладают свойствами дистрибутивности и ограниченности, т.е.
4. (aÙb)Úc = (aÚc) Ù (bÚc); (aÚb) Ù c = (aÙc) Ú (bÙc),
5. 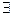 0: aÙ0 = 0 и
0: aÙ0 = 0 и 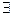 1: aÚ1 = 1;
1: aÚ1 = 1;
И для каждого а существует элемент 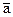 , называемый дополнением:
, называемый дополнением:
6. "а$ 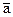 : аÙ
: аÙ 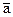 = 0, аÚ
= 0, аÚ 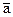 =1,
=1,
то мы получаем алгебру, которая называется алгеброй Буля, и в которой, помимо установленных свойств, выполняются следующие:
7. Дополнение единственно.
8. Дополнение инволютивно:
9. Грани дополняют друг друга:
10. Выполняются законы де Моргана.
Множество М, в котором для любых элементов a, b существует inf(a,b) (sup(a,b)), называется нижней (верхней) полурешеткой. Если существуют обе грани, то множество называется решеткой
NB. 1) Решетка интересна тем, что из упорядоченного множества без введения каких-то дополнительных структур (операций) получилась алгебра. При этом на линейно упорядоченном множестве алгебра тривиальна.
2) Полученная алгебра решётки изоморфна алгебре множеств.
Решёткой называется частично упорядоченное множество, в котором для любых двух элементов a и b существуют точная верхняя грань – sup(a,b)=aÚb и точная нижняя грань – inf(a,b)=aÙb Инфинум и супремум оказываются, таким образом, бинарными операциями на М, а решётка – алгебраической системой {M; 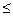 ; Ú;Ù}. Операции взятия точных граней ассоциативны, поэтому можно определить их для любого подмножества множества М.
; Ú;Ù}. Операции взятия точных граней ассоциативны, поэтому можно определить их для любого подмножества множества М.
ê Любое линейно упорядоченное множество (например, ¢) можно превратить в решётку, определив для любых a, b: aÚb = max (a,b), aÙb=min (a,b).
ê Определим на N отношение частичного порядка a 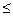 b, если a делит b. Тогда aÚb – наименьшее общее кратное а и b, а aÙb – наибольший общий делитель а и b. Например, 9Ú12=36, 9Ù12=3, а 5Ú7=35, 5Ù7=1.
b, если a делит b. Тогда aÚb – наименьшее общее кратное а и b, а aÙb – наибольший общий делитель а и b. Например, 9Ú12=36, 9Ù12=3, а 5Ú7=35, 5Ù7=1.
ê Система всех подмножеств любого множества U (булеан 2U) частично упорядочена по включению Í. Таким образом, булеан является решёткой, элементами которой являются множества, а операциями инфинум и супремум – обычные теоретико-множественные операции пересечения и объединения.
ê Рассмотрим множество Bn двоичных векторов длины n, частично упорядоченное следующим образом: a =(α1, …, αn) ≤ b = (β1, …, βn), если в а единицы стоят на всех тех местах, на которых они стоят в b (и, быть может, ещё на некоторых). Например, (010) ≤(011), а (010) и (100) не сравнимы (запятые между компонентами вектора здесь и далее опускаем). Множество Bn, упорядоченное таким образом, является решёткой; в ней aÚb – это вектор, в котором единицы стоят на тех (и только тех) местах, где есть единицы либо в а, либо в b, а aÚb – это вектор, в котором единицы стоят на тех и только тех местах, где единицы есть и в а, и в b. Например, (010) Ú (100) = (110), (010) Ù (100)=(000).
ê Ранее нами было установлено взаимно однозначное соответствие между множеством Bn и булеаном 2Ô произвольного множества Ô мощности n. Легко проверить, что это соответствие является изоморфизмом решёток; таким образом, решетки, описанные в данном и предыдущем примере, изоморфны.
ê Когда упорядоченное множество не является решёткой? Тогда, когда какие-либо два элемента не имеют супремума или инфинума. А это возможно в двух случаях: 1) когда нет какой-то из граней; 2) когда грань не единственна. [На рис. а элементы (d,e), (c,d) не имеют верхней грани, элементы (b,c) не имеют нижней грани. На рис. б (b,c) имеют две наименьшие и несравнимые верхние грани, (d,e) имеют две наибольшие нижние грани.]
ê Решётка, в которой пересечение и объединение существуют для любого подмножества её элементов, называется полной. – Конечная решётка всегда полна. Объединение всех элементов полной решётки – это максимальный элемент, называемый единицей решётки. Пересечение всех элементов полной решётки – это минимальныё элемент, называемый нулём решётки. Решетка–булеан 2Ô – всегда полна, даже для бесконечного множества Ô. Единицей этой решётки служит само множество Ô (универсум), содержащее все свои подмножества, нулём – пустое множество ¯.

 f
f




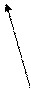
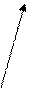 d e d e
d e d e
 |
b


 c b c
c b c
a a
Рис. а. Рис. б
 2015-06-24
2015-06-24 1752
1752








