Под знаком неизвестной функции могут стоять дробно-линейные выражения вида 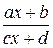 . Такие дроби полностью определяются заданием матрицы
. Такие дроби полностью определяются заданием матрицы 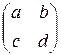 , составленной из коэффициентов a, b, c, d.
, составленной из коэффициентов a, b, c, d.
Пример 15. Найти функцию f, определенную при
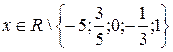
и удовлетворяющую уравнению
 (5.1)
(5.1)
Решение. Отыщем подстановку, переводящую выражения, стоящие под знаком неизвестной функции f в уравнении (5.1), друг в друга.
Для этого положим 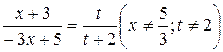 . Отсюда
. Отсюда
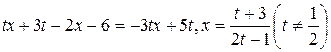 .
.
Кроме того, 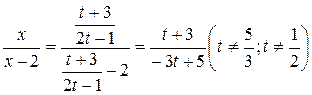 .
.
Следовательно, подстановка 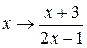 – искомая. Уравнение (5.1) примет вид
– искомая. Уравнение (5.1) примет вид
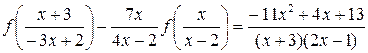 . (5.2)
. (5.2)
В уравнении (5.1) 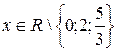 Подстановка
Подстановка 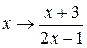 переводит точки
переводит точки 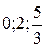 соответственно в точки
соответственно в точки 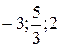 . Кроме того, из характера подстановки вытекает
. Кроме того, из характера подстановки вытекает 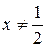 . Поэтому в уравнении (5.2)
. Поэтому в уравнении (5.2) 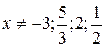 . Область допустимых значений х в системе, составленной из уравнений (5.1) и (5.2), является пересечением соответствующих областей каждого из уравнений (5.1) и (5.2), т. е.
. Область допустимых значений х в системе, составленной из уравнений (5.1) и (5.2), является пересечением соответствующих областей каждого из уравнений (5.1) и (5.2), т. е. 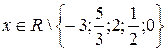 . Исключая из этой системы
. Исключая из этой системы 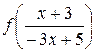 , получим
, получим
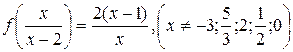
Обозначив 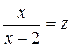 , получим
, получим 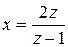 . Из условия
. Из условия 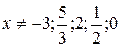 получаем
получаем 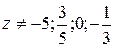 , а также
, а также 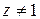 , что определяется видом подстановки.
, что определяется видом подстановки.
Подстановка 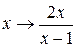 дает
дает 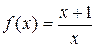 . Итак, функция
. Итак, функция 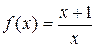 с областью определения
с областью определения 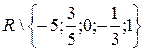 является решением примера 15, что и подтверждается проверкой. Сужение области определения искомой функции удалением точек
является решением примера 15, что и подтверждается проверкой. Сужение области определения искомой функции удалением точек 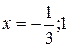 вызвано методом решения уравнения. Несложные вычисления показывают, что функция
вызвано методом решения уравнения. Несложные вычисления показывают, что функция 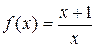 ,
, 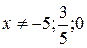 , удовлетворяет исходному уравнению.
, удовлетворяет исходному уравнению.
|
|
|
В самом деле, полагая в (5.1) 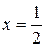 , получим
, получим 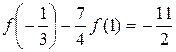 .
.
Значения функции 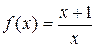 ,
, 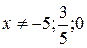 , в точках
, в точках 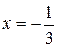 и 1 соответственно равны
и 1 соответственно равны 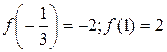 и удовлетворяют приведенному соотношению.
и удовлетворяют приведенному соотношению.
Более того, решение уравнения (5.1) в классе функций таких, что 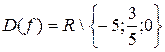 имеет вид
имеет вид
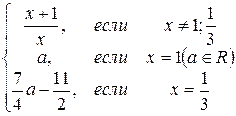
Уравнение (5.1) решено, так как найдена подстановка 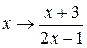 переводящая дробно-линейные функции
переводящая дробно-линейные функции 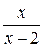 и
и 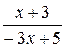 , получим друг в друга. На языке матриц это означает, что найдена матрица
, получим друг в друга. На языке матриц это означает, что найдена матрица 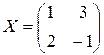 такая, что АХ = kB; BX =lA, где
такая, что АХ = kB; BX =lA, где
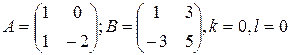 .
.
Возникает вопрос, для любых ли дробно-линейных функций существует аналогичная подстановка; другими словами, для любых ли матриц А и В существует матрица X, удовлетворяющая уравнениям
АХ = kВ, (5.3)
ВХ = lА (5.4)
при некоторых k, l, отличных от нуля.
Предполагая, что такая матрица существует, из уравнений (5.3) и (5.4) получим: (lА)X = (lk)В, (ВХ)X = (lk)В,
BX2 = (lk)B (5.5)
Предположим, что функции, соответствующие матрицам А и В, отличны от констант. Тогда, как показано выше, для А и В существуют обратные матрицы. Умножим обе части равенства (5.5) слева на В-1. Получим
B-1BX2= B-1lkB; EX2 = (lk)E; X2 = mE, где m=lk
Найдем общий вид матрицы 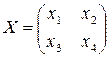 такой, что
такой, что 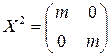 , т.е.
, т.е.
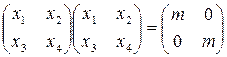 ,
,
при некотором m ≠ 0. Заметим, что х1x4 – х2х3 ≠ 0. Из правила умножения и условия равенства матриц имеем:
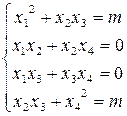
Вычитая из первого уравнения четвертое, получим 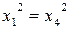 т. е.
т. е. 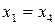 , либо
, либо 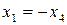 .
.
Если 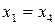 , то
, то 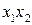 = 0 и
= 0 и 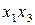 = 0, что приводит к матрицам вида
= 0, что приводит к матрицам вида 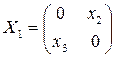 или
или 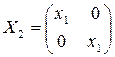 . Если же
. Если же 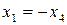 то придем к матрице
то придем к матрице 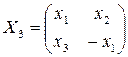
Проверкой убеждаемся, что матрицы Х2 и Х3 удовлетворяют уравнению X2=mЕ при некотором m. Матрица Х3 при х1 = 0 дает X1.
|
|
|
Итак, матрицы вида 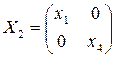 и
и 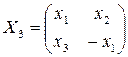 и только они удовлетворяют уравнению X2 = mE, m ≠ 0. Из (5.4) имеем X = lВ-1А. Поэтому, если матрица В-1А имеет вид Х2 или Х3, то она удовлетворяет каждому из уравнений (5.3), (5.4).
и только они удовлетворяют уравнению X2 = mE, m ≠ 0. Из (5.4) имеем X = lВ-1А. Поэтому, если матрица В-1А имеет вид Х2 или Х3, то она удовлетворяет каждому из уравнений (5.3), (5.4).
Теперь изложим один из способов решения функционального уравнения вида
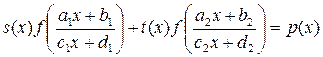 (5.6)
(5.6)
где s(x), t(x), р (х) — некоторые данные функции,
Решая матричное уравнение вида А = ВХ, где 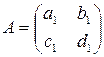 ,
, 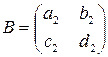 , получим X = В-1А,
, получим X = В-1А,
Если матрица X имеет вид 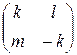 , то подстановка
, то подстановка 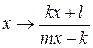 в (5.6) даст второе уравнение относительно неизвестных
в (5.6) даст второе уравнение относительно неизвестных
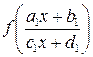 ,
, 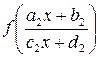
Если полученная система имеет решение, то из нее найдем выражение для 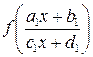 . Последнее дает возможность найти f(x). Как обычно, обязательной частью решения является проверка. Случай
. Последнее дает возможность найти f(x). Как обычно, обязательной частью решения является проверка. Случай 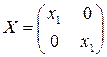 тривиален, А = х1В, т. е. выражения, стоящие в (5.6) под знаком f, совпадают.
тривиален, А = х1В, т. е. выражения, стоящие в (5.6) под знаком f, совпадают.
Пример 16. Найти функцию f, определенную при 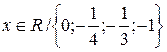 , удовлетворяющую уравнению
, удовлетворяющую уравнению
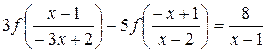 (5.7)
(5.7)
Решение. Решаем матричное уравнение AХ = В, где 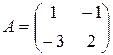 ;
; 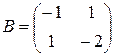 . Для матрицы A обратной является матрица
. Для матрицы A обратной является матрица 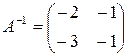 . Тогда
. Тогда 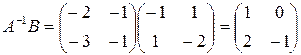 . Матрица X имеет вид
. Матрица X имеет вид 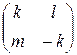 , поэтому применим к уравнению (5.7) подстановку
, поэтому применим к уравнению (5.7) подстановку 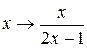 . Последнюю удобно выполнять с помощью матриц. Правой части уравнения (5.7) соответствует матрица
. Последнюю удобно выполнять с помощью матриц. Правой части уравнения (5.7) соответствует матрица 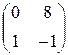 . Применение к ней подстановки
. Применение к ней подстановки 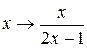 равносильно умножению
равносильно умножению 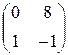 справа на
справа на 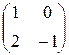 . В результате получим
. В результате получим 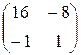 . Таким образом, из уравнения (5.7) находим
. Таким образом, из уравнения (5.7) находим
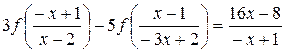 (5.8)
(5.8)
Исключив из системы, составленной из уравнений (5.7) и (5.8) 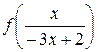 имеем
имеем
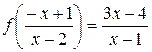 (5.9)
(5.9)
Из (5.7) видим, что 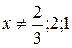 . Подстановка сохранила эти ограничения. Кроме того,
. Подстановка сохранила эти ограничения. Кроме того, 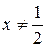 .
.
Положим 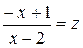 . Так как
. Так как 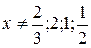 , то
, то 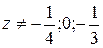 . Отсюда
. Отсюда 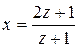 . Заменяя
. Заменяя 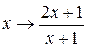 , из (5.9) получим
, из (5.9) получим
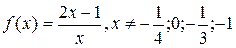 .
.
Проверка показывает, что эта функция удовлетворяет условию задачи:
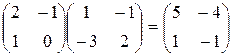
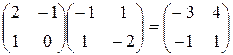
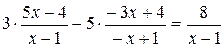
 2015-06-24
2015-06-24 554
554








