2015-06-26
354
Для нахождения решения краевой задачи (8.2) можно численно построить решение дифференциального уравнения, представимое в виде
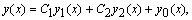
где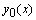 
— какое-либо решение неоднородного уравнения
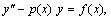
а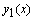 
и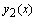 
— два любые линейно независимые решения однородного уравнения 
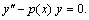Постоянные 
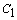и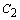 
находятся из граничных условий задачи (8.2).
Так как решения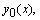 
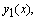
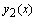произвольны, то их можно построить различными способами. Например, можно задать какие-то начальные условия и решить одну задачу Коши для неоднородного и две задачи Коши для однородного уравнений. Эти условия, в частности, могут быть такими:
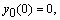
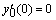— для неоднородного уравнения;
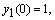
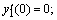
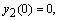
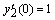— для однородного уравнения.
Однако при реализации этого способа, например, в случае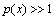 
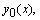
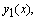
для рассматриваемого уравнения могут возникнуть трудности, связанные с неустойчивостью задачи Коши. В этом случае можно попытаться построить 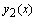с помощью решения одной краевой задачи для неоднородного уравнения и двух краевых задач для однородного уравнения. Краевые условия для этих задач могут быть, например, следующими:
|
|
|
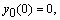
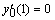— для неоднородного уравнения;
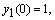
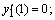
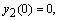
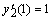— для однородного уравнения.
Эти задачи могут быть решены методом прогонки. Условия устойчивости метода прогонки при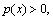 
как легко проверить, выполнены. Этот подход может оказаться полезным, если краевые условия таковы, что для исходной задачи (8.2) метод прогонки применен быть не может.
Отметим, что с учетом специфики краевых условий исходной задачи можно строить общее решение вида
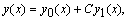
где 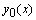— некоторое решение неоднородного уравнения, а 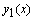— некоторое решение однородного уравнения.
