Методические указания к заданию 1

Рассмотрим пример графического и аналитического решения задачи НПР.

Пусть дана целевая функция (ЦФ):

Z = (х₁-7)² + (х₂-4)², (4.1)

а также ограничения:

х₁+х₂ ≤ 10,

2х₁+х₂ ≥ 12,

х₁-х₂ ≥ 2,

х₁-х₂ ≤ 4

х₁≥ 0, х₂≥ 0

Требуется максимизировать ЦФ.

Чтобы найти решение графически, вначале следует изобразить многоугольник (полигон) допустимых решений. Построение области допустимых решений (ОДР) осуществляется так же, как в задачах линейного программирования [1].

Для построения ОДР вначале следует записать уравнение х₁ + х₂ = 10. Оно получается из первого неравенства заменой знака «≤» на знак «=». Для построения прямой линии х₁ + х₂ = 10 достаточно иметь две точки. Первую точку удобно взять при х₁ = 0, а вторую точку при х₂ = 0. Используя остальные ограничения, аналогично строят другие прямые линии.

Нетрудно заметить, что прямые х₁ = 0 и х₂ = 0 (пятое и шестое ограничения) являются осями координат х₁ и х₂.

Затем следует отметить стрелками полуплоскости, которые удовлетворяют заданным неравенствам. Направление стрелок определяют знаки неравенств [1]. Область, удовлетворяющая всем четырем неравенствам, будет областью допустимых решений (трапеция ABCD). На рис. 4. 1 ОДР выделена серым цветом.

.

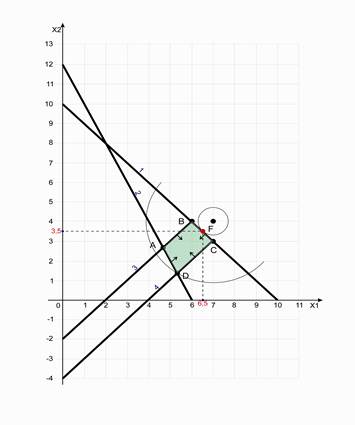
Рисунок 4.1- Полигон допустимых решений

Теперь необходимо построить график ЦФ. Для этого с помощью уравнения (4.1) следует отметить центр окружности. В данном примере х₁ = 7 и х₂ = 4. Затем с помощью циркуля нужно построить несколько окружностей, увеличивая радиус до тех пор, пока окружность не коснется какой либо точки ОДР. В этой точке будет минимум ЦФ. За тем с помощью циркуля следует найти наиболее удаленную от центра окружности точку ОДР. В этой точке будет максимум ЦФ.

Из рисунка 4.1 видно, что минимум ЦФ находится в точке F, а максимум – в точке D. Определим приблизительно координаты точки F: х₁ = 6,5, х₂ = 3,5. Значение целевой функции в этой точке Z = 0,5. Приблизительные значения координат точки D: х₁ = 5,3, х₂ = 1,4. Приблизительное значение ЦФ в этой точке Z = 9,65.

На основании приближенного графического решения задачи НПР найдём аналитически точный ответ. Для этого, из уравнения целевой функции Z = (х1-7)²+(х2-4)² найдем производные по х₁ и х₂

Производная по х₁:

Z^| = 2(х₁-7) + 2(х₂-4)²* х₂^| =0 (1)

Z^| =0

Выразим из уравнения (1) производную х₂^|

х₂^| = -(х₁-7/ х₂-4)

Определим тангенс угла наклона (производную) для прямой х₁+ х₂ = 10

х₂^| = -1

-(х₁-7/ х₂-4) = - 1

х₁-7 = х₂-4

Решим систему уравнений

-х₁+ х₂ = 3

х₁+ х₂ = 10

2 х₁₌ 13,

х₁= 6,5

х₂ = 3,5

Полученные значения х₁ и х₂ подставляем в ЦФ

Z = (х₁-7)²+(х₂-4)²

Таким образом, максимальное значение ЦФ Z=0,5.

4.2 Методические указания к лабораторной работе № 2

Пример решения задачи НПР с помощью системы Mathcad

Пусть дана целевая функция (ЦФ)

Z = х₁² - 20х₁ - 20х₂ + x₂²,

а также ограничения:

х₁ + х₂ = 11

х₁ ≥ 0, х₂ ≥ 0

Требуется минимизировать ЦФ.

Чтобы найти решение методом множителей Лагранжа, вначале следует сформировать функцию Лагранжа:

F(х_1, х_2, λ) = х₁² - 20х₁-20х₂ + x₂²+λ (11- х₁ - х₂ )

Затем найдем производные по х_1, х_2, λ:

dF/ dх₁=2х₁-20

dF/ dх₂=2х₂-20

dF/ dλ =11- х₁ - х₂

Далее найденные производные следует приравнять к нулю и решить полученную систему линейных алгебраических уравнений.

2х₁-20 = 2х₂-20

2х₁-2х₂= 0

Решим систему уравнений

х₁-х₂= 0

х₁ + х₂ = 11

х₁= 5.5

х₂= 5.5

В ответ записываем значения х₁ = 5.5, х₂ = 5.5

4.3 Методические указания к лабораторной работе № 3

Задачи математического программирования можно решать с помощью системы Mathcad. Ниже приведен текст программы с комментариями (полужирный шрифт).

Зададим ЦФ:

Z(x1, x2):= (х1-7)²+ (х2-4)²

Зададим произвольные начальные значения переменным:

x1:= 0

x2:= 0

Начало блока вычислений

Given

Опишем ограничения:

х₁+х₂ ≤ 10

2х₁+х₂ ≥ 12

х₁-х₂ ≥ 2

х₁-х₂ ≤ 4

х₁≥ 0

х₂≥ 0

Выполним операцию минимизации:

P: = Minimize (Z, x1, x2)

Выведем на экран значения найденных переменных:

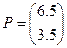
Вычислим целевую функцию:

Z (P₀, P₁) = 0.5

Итак, оптимальные значения переменных:

х1 = 6,5, х2 = 3,5. Значение ЦФ Z = 0,5

4.4 Методические указания к заданию 4

Задачи математического программирования можно решать с помощью системы Mathcad. Ниже приведен пример программы с комментариями (полужирный шрифт).

Зададим ЦФ:

Z(x1,x2, x3):= 3x1 + 4 х₂² + 2x3

Зададим произвольные начальные значения переменным:

x1:= 0

x2:= 0

x3:= 0

Начало блока вычислений

Given

Опишем ограничения:

x1 ≥ 0

x2 ≥ 0

x3 ≥ 0

15 х₁² + 16 х₂²-17 x₃ ≤ 120

18 х₁² - 19 х₂²+20 x₃ ≤ 130

-21 х₁² + 22 х₂²+23 x₃ ≤ 140

Выполним операцию максимизации:

P: = Maximize(Z,x1,x2,x3)

Выведем на экран значения найденных переменных:

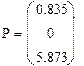
Вычислим целевую функцию:

Z(P₀, P₁,P₂) = 14.25

Итак, оптимальные значения переменных: х1 = 0.835, х2 = 0, x3 = 5,873. Максимальное значение ЦФ Z = 14.25

Построим трехмерный график, который показывает ограничения и оптимальное положение целевой функции.

Присвоим значение ЦФ переменной R:

R:= Z(P₀, P₁,P₂)

Создадим циклы для изменения переменных х₁ и х₂:

x1:=0..P₀ + 5

x2:=0..P₁ + 5

Выразим переменную х₃ из трех ограничений и целевой функции:

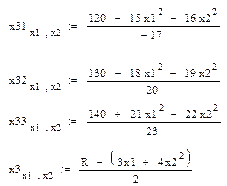
Графическая иллюстрация полученного решения

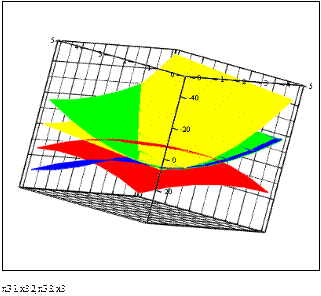
Рисунок 4.2 - Трехмерный график

4.5 Методические указания к заданию 5

Пример решения двухмерной задачи градиентным методом

Требуется методом градиента найти минимум функции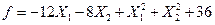

при ограничениях

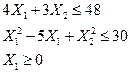
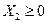
Построим ограничения, выберем область допустимых значений. Возьмем в допустимой области произвольную точку, например 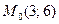. Она действительно принадлежит заданной области, т.к. подставив координаты точки 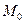в ограничения, получим, что знак неравенства сохраняется

=

=

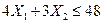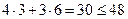
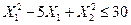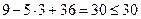
Находим частные производные функции 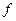по переменным 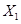, , 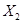т.е.

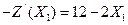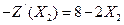, . Составим градиент заданной функции в заданной точке

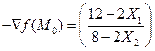
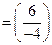
Поскольку 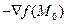= 0, то 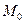не является точкой экстремума.

Вычислим координаты новой точки. Для определения координат точки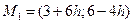

необходимо определить значение параметра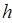

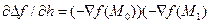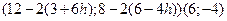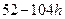= = = 0

При 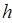= 0,5 изменение 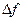значения функции 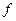достигает наибольшей величины. Получающаяся при этом точка

= = =

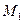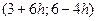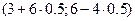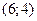
Точка 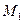принадлежит допустимой области

=

=

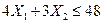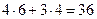
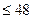
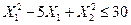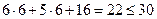
В точке 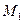антиградиент .

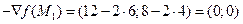Значит никакими перемещениями из точки 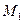функцию уменьшить нельзя и 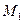- искомая точка минимума.

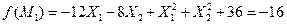
Ответ: , ,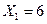

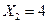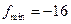
Заключение

В данной работе разработано пять лабораторных работ по нелинейному программированию (НПР):

1) Решение двухмерных задач нелинейного программирования графическим и аналитическим методами.

2) Решение двухмерных задач НПР с помощью системы Mathcad.

3) Решение двухмерных задач НПР методом множителей Лагранжа.

4) Решение трехмерных задач НПР с помощью системы Mathcad.

5) Решение задач НПР градиентным методом.

В каждой лабораторной работе разработано по тридцать два варианта, приведен пример решения с подробным описанием, построен трехмерный график. Каждый из разработанных вариантов проверен, выполнен расчет и подготовлены ответы для преподавателей, которые будут проводить занятия.

При решении задач нелинейного программирования в разработанном цикле лабораторных работ используются разные методы. Ни один из рассмотренных методов нелинейного программирования не является универсальным. При выполнении разработанных лабораторных работ студенты получают прочные навыки в решении задач математического программирования.

Расчёт сравнительной экономической эффективности разработки лабораторных работ показывает высокие экономические показатели.

Материалы данного дипломного проекта предполагается в ближайшее время опубликовать в виде методических указаний на выполнение лабораторных работ.