Определение 1. Минором порядка k матрицы 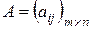 называется определитель порядка k, составленный из элементов, стоящих на пересечении k строк и k столбцов.
называется определитель порядка k, составленный из элементов, стоящих на пересечении k строк и k столбцов.
Например, для матрицы 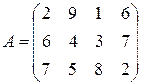 минорами первого порядка являются:
минорами первого порядка являются: 
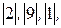 …., т.е. определители первого порядка, составленные из элементов матрицы. Минорами второго порядка являются определители:
…., т.е. определители первого порядка, составленные из элементов матрицы. Минорами второго порядка являются определители: 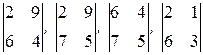 , …., т.е. определители второго порядка, составленные из элементов, стоящих на пересечении двух строк и двух столбцов. Минорами третьего порядка являются:
, …., т.е. определители второго порядка, составленные из элементов, стоящих на пересечении двух строк и двух столбцов. Минорами третьего порядка являются: 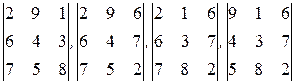 . Миноров четвертого порядка у неё быть не может, так как строк всего 3.
. Миноров четвертого порядка у неё быть не может, так как строк всего 3.
Для практических приложений важное значение имеет порядок миноров матрицы, отличных от нуля.
Определение 2. Наивысший порядок миноров матрицы 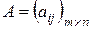 , отличных от нуля, называется рангом матрицы А.
, отличных от нуля, называется рангом матрицы А.
Обозначение: rang(A) или r(A).
Замечание. На практике, для определения ранга матрицы, как правило, поступают следующим образом: смотрят, миноры каких порядков можно составить и, начиная с минором наивысшего порядка проводят анализ: если среди них ненулевые, если есть, то ранг матрицы равен числу, соответствующему порядку этих миноров; если все они – нулевые, то анализируют миноры порядка на единицу меньше.
|
|
|
Пример 1. Определите ранги матриц: а) 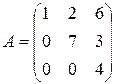 ; б)
; б) 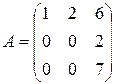 .
.
Решение. а) Заметим, что наивысший порядок миноров, которые можно составить для данной матрицы – 3, это минор, составленный из всех элементов матрицы. Определим его величину, используя правило вычисления определителей треугольного вида (смотрите параграф «Определители»):
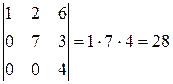 .
.
Минор отличен от нуля, следовательно, ранг матрицы равен 3.
б) В этом случае наивысший порядок миноров, которые можно образовать из элементов матрицы, также равен 3. Но величина соответствующего определителя, вычисленная, как и в предыдущем случае, с помощью правила вычисления определителей треугольного вида, равна нулю:
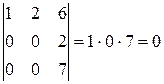 .
.
Других миноров третьего порядка для данной матрицы составить нельзя, следовательно, ранг матрицы не может быть равен 3.
Проверим, есть у данной матрицы миноры второго порядка, отличные от нуля.
Заметим, что 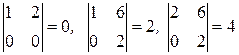 .
.
Так как среди миноров второго порядка есть ненулевые миноры, то наивысший порядок миноров, отличных от нуля, для данной матрицы, - 2. Следовательно, ранг матрицы равен 2.
Замечание. В тех случаях, когда число строк или столбцов матрицы не превышает трех, особых затруднений с определением ранга не возникает. Но когда приходится проводить анализ значений определителей более высоких порядков (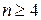 ), простой перебор миноров, начиная с миноров наивысшего порядка, может потребовать много времени и усилий. Решение задачи можно упростить, если воспользоваться следующей теоремой.
), простой перебор миноров, начиная с миноров наивысшего порядка, может потребовать много времени и усилий. Решение задачи можно упростить, если воспользоваться следующей теоремой.
|
|
|
Теорема 1. Если матрица А эквивалентна матрице В, то 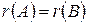 , т.е. элементарные преобразования не изменяют ранга матрицы.
, т.е. элементарные преобразования не изменяют ранга матрицы.
Доказательство. Справедливость данного утверждения следует из свойств определителей: элементарные преобразования не могут нулевой определитель превратить в ненулевой и наоборот.
Замечание. Эта теорема дает более простой алгоритм определения ранга матрицы: используя элементарные преобразования, матрицу сначала приводят к треугольному виду или иному другому виду, позволяющему легко определить ранг матрицы с помощью рассмотренного выше (смотрите Пример 1) алгоритма.
Пример 2. Определите ранг матрицы  .
.
Решение. Сначала, используя элементарные преобразования, приведем матрицу к треугольному виду. Для чего предварительно поменяем местами первую и вторую строки матрицы, а затем к элементам третьей сроки прибавим соответствующие элементы первой, умноженные на 3, а к элементам пятой строке прибавим соответствующие элементы первой строки, первую, умноженные на 2:
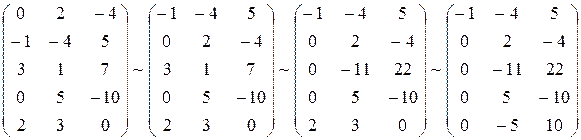 .
.
Перед следующим шагом (получением нулей во втором столбце) предварительно разделим элементы второй, третьей, четвертой и пятой строк на 2, -11, 5, -5 соответственно (данная операция равносильна умножению элементов данных строк на 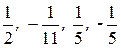 соответственно).
соответственно).
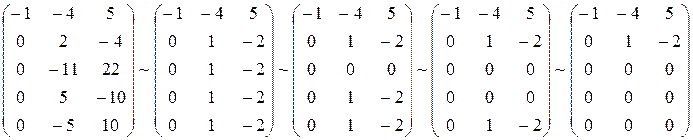 .
.
Миноры наивысшего порядка, которые можно составить для данной матрицы, – это миноры третьего порядка, но все они будут равны нулю, так как у матрицы, получившейся после элементарных преобразований только две ненулевые строки.
Нетрудно заметить, что минор 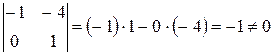 . Следовательно, ранг получившейся матрицы равен 2, а так как она эквивалентна исходной (получается из неё при помощи элементарных преобразований), то ранг исходной матрицы тоже равен 2.
. Следовательно, ранг получившейся матрицы равен 2, а так как она эквивалентна исходной (получается из неё при помощи элементарных преобразований), то ранг исходной матрицы тоже равен 2.
Замечание. Существует еще один алгоритм определения ранга, который называется методом окаймляющих миноров. При желании с ним можно ознакомиться в учебнике Курош А.Г Курс высшей алгебры. – М: Наука, 1971. – С.73-74.
Определение 3. Миноры матрицы, отличные от нуля, порядок которых равен рангу матрицы, называются базисными минорами.
Теорема 2. Если 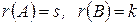 , то
, то 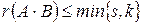 , т.е. ранг произведения матрицы-произведения не выше ранга каждого из сомножителей.
, т.е. ранг произведения матрицы-произведения не выше ранга каждого из сомножителей.
Доказательство. Справедливость данного утверждения легко доказать, опираясь на правило умножения матриц. Более подробно доказательство представлено в учебнике Курош А.Г. Курс высшей алгебры. – М: Наука, 1971, С. 101.
Теорема 3. Если 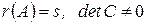 , то
, то 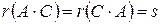 .
.
Доказательство.
Заметим, что с одной стороны 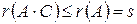 ; с другой стороны:
; с другой стороны:
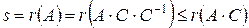 . Откуда и следует, что
. Откуда и следует, что 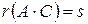 .
.
Аналогично, 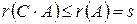 , в тоже время:
, в тоже время: 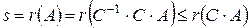 , откуда и следует, что
, откуда и следует, что 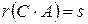 .
.
Теорема доказана.
Определение 4. Квадратные матрицы А и В, связанные соотношением:
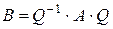 , (1)
, (1)
где 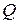 - невырожденная матрица, называются подобными матрицами.
- невырожденная матрица, называются подобными матрицами.
Определение 5. Операция перехода от матрицы А к матрице В по формуле (1) называется трансформированием матрицей 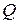 .
.
Следствие 1. Если 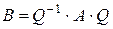 , где
, где 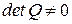 , то
, то 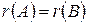 .
.
Доказательство. Следует из теоремы 3.
Замечание. Понятие ранга матрицы можно ввести также, используя понятие линейной независимости (зависимости) её строк или столбцов. Этот вопрос будет обсужден ниже (при изучении темы «Линейные пространства»).
Умение определять ранги матриц оказывается полезным как при решении систем m уравнений с n неизвестными, так и при решении систем n уравнений c n неизвестными, когда рассмотренные выше правила, оказываются неприменимыми (определитель из коэффициентов при неизвестных равен нулю)
Теорема 4 (теорема Кронекера-Капелли) Система m линейный уравнений с n неизвестными вида (2):
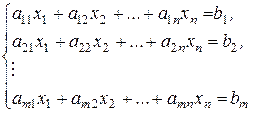 (2)
(2)
совместна, тогда и только тогда, когда ранг матрицы 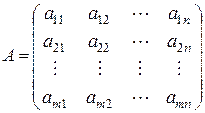 из коэффициентов при неизвестных системы равен рангу расширенной матрицы
из коэффициентов при неизвестных системы равен рангу расширенной матрицы 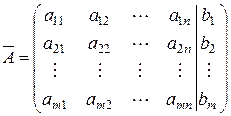 , т.е.
, т.е. 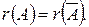
Доказательство. Изучите самостоятельно. Смотрите, например, Курош А.Г. Курс высшей алгебры. – М: Наука, 1971. С. 78 – 81.
|
|
|
Замечание. Ранее мы уже отмечали, что однородная система всегда совместна, так как у неё есть нулевое решение. Теорема Кронекера – Капелли это тоже подтвердит, так как добавление нулевого столбца свободных членов не может привести к увеличению ранга матрицы.
Следствие 2. Если система вида (2) совместна и 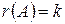 , то
, то 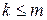 .
.
Следствие 3. Если система вида (2) совместна и 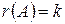 , то при
, то при 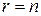 система является определенной (имеет единственное решение); при
система является определенной (имеет единственное решение); при 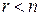 система является неопределенной (имеет бесчисленное множество решений).
система является неопределенной (имеет бесчисленное множество решений).
Замечание. На практике, чтобы не выполнять лишней работы, исследование рангов матрицы из коэффициентов и расширенной матрицы проводят одновременно. Для этого выписывают расширенную матрицу системы, отделяя столбец свободных членов вертикальной чертой, и работая только со строками, приводят расширенную матрицу к треугольному виду или виду, позволяющему без труда определить ранг матрицы. В этом случае элементы до вертикальной черты соответствуют элементам матрицы эквивалентной матрице из коэффициентов.
Пример 3. Исследовать на совместность систему четырех уравнений с пятью неизвестными:
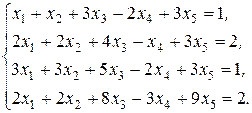 (3)
(3)
Решение. Выпишем расширенную матрицу системы (3), отделяя столбец свободных членов вертикальной чертой, и приведем её к треугольному виду, применяя элементарные преобразования только к строкам матрицы:
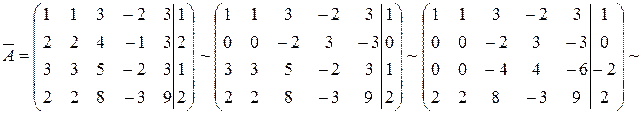
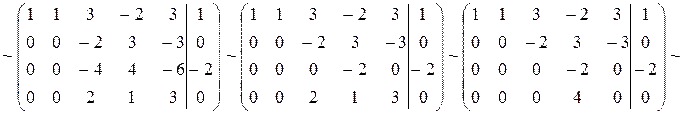
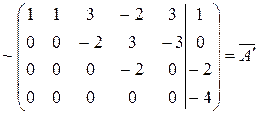 .
.
Матрица 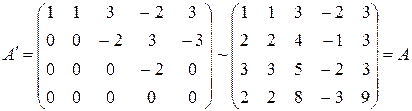 ,
,
её ранг равен 3, так как ненулевых миноров четвертого порядка у неё нет, а примером минора третьего порядка, отличного от нуля является минор 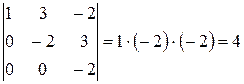 . Следовательно,
. Следовательно, 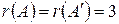 .
.
Матрица 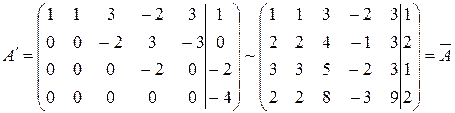 ,
,
ее ранг равен четырем, так как, минор
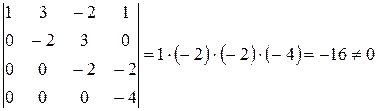 . Следовательно,
. Следовательно, 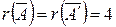 .
.
Так как 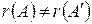 , то система (3) – несовместна.
, то система (3) – несовместна.
Замечание. Увидеть, что рассматриваемая система не имеет решений можно и, не исследуя ранги. Достаточно заметить, что если выписать систему, соответствующую получившейся матрице 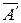 , то она примет вид (4):
, то она примет вид (4):
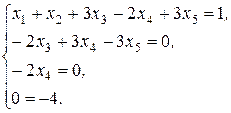 (4)
(4)
Четвертое уравнение системы (4) не является верным равенством. Следовательно, система (4) решений не имеет, т.е является несовместной.
Пример 4. Исследовать систему на совместность систему трех уравнений с четырьмя неизвестными:
|
|
|
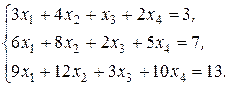 (5)
(5)
В случае совместности постройте общее решение.
 2015-07-03
2015-07-03 4962
4962







