 Квантовый принцип суперпозиции является центральным принципом квантовой физики. Применительно к описанию состояний фотона его можно пояснить так. Если фотон может попасть в состояние несколькими способами, результирующая амплитуда попадания в данное состояние равна векторной сумме амплитуд попадания каждым из способов. Надо иметь в виду, что амплитуды складываются только в том случае, когда принципиально невозможно различить, каким из способов произошло попадание в данное состояние. Если же при проведении эксперимента использовать какое либо устройство, позволяющее определить, каким из способов произошло попадание в конечное состояние, то амплитуды не складываются – складываются вероятности осуществления всех способов. В этом случае квантовой интерференции амплитуд вероятности нет.
Квантовый принцип суперпозиции является центральным принципом квантовой физики. Применительно к описанию состояний фотона его можно пояснить так. Если фотон может попасть в состояние несколькими способами, результирующая амплитуда попадания в данное состояние равна векторной сумме амплитуд попадания каждым из способов. Надо иметь в виду, что амплитуды складываются только в том случае, когда принципиально невозможно различить, каким из способов произошло попадание в данное состояние. Если же при проведении эксперимента использовать какое либо устройство, позволяющее определить, каким из способов произошло попадание в конечное состояние, то амплитуды не складываются – складываются вероятности осуществления всех способов. В этом случае квантовой интерференции амплитуд вероятности нет.
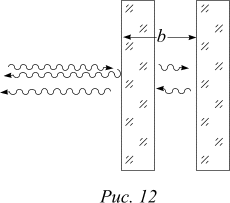
Пример квантовой интерференции. Пучок фотонов одной и той же энергии направим на две параллельные друг другу плоскопараллельные пластинки (интерферометр Фабри-Перо). Будем регистрировать отраженные от системы фотоны.
|
|
|
Описание опыта на классическом языке выглядит так. Электромагнитная волна частично проходит и частично отражается от первой пластинки. С прошедшей частью происходит то же самое. Отраженная волна представляет собой суперпозицию двух волн - отраженной от первой и отраженной от второй пластинки. Если разность хода отраженных волн равна целому числу волн, то будет наблюдаться усиление отраженного света. Если же разность хода отраженных волн равна нечетному числу полуволн, то будет наблюдаться ослабление отраженного света. Поэтому при плавном изменении расстояния между пластинками должно наблюдаться попеременное усиление и ослабление отраженного света. Это предсказание согласуется с опытными данными.
Оказывается, все предсказания на основе классической волновой теории, подтверждаемые экспериментально, следуют и из квантовой теории. Проведем квантовые рассуждения. Падающий на первую пластинку фотон имеет амплитуду отразиться, обозначим ее через a1, и имеет амплитуду пройти, обозначим ее через b1. Очевидно, a1 и b1 должны удовлетворять условию ç a1 ç 2+ ç b1 ç 2=1. Амплитуда вероятности Y2 фотону, отраженному от второй пластинки, выйти из первой пластинки имеет фазу, большую фазы амплитуды вероятности отражения от первой пластинки Y1=a1 на Dj=2kb (для простоты не учитываем показатель преломления пластинок, то есть считаем пластинки бесконечно тонкими), потому что точка выхода фотона, отраженного от второй пластинки, отстоит от точки отражения от первой пластинки вдоль траектории фотона на двойное расстояние между пластинками. Детектор фотонов, установленный перед пластинками, принципиально не может отличить, от первой или второй пластинки отразился фотон. Поэтому, результирующая амплитуда вероятности того, что фотон отразится от системы пластинок, равна векторной сумме амплитуд Y1 и Y2. Из рисунка видно, что при разности фаз амплитуд вероятности, равной целому числу 2p, сумма амплитуд равна сумме длин стрелок, а при разности фаз, равной нечетному числу p, сумма амплитуд равна разности длин стрелок. В первом случае вероятность прохождения равна квадрату суммы длин стрелок, а во втором - квадрату разности длин стрелок. В общем случае вероятность отражения P вычислится по теореме косинусов
P= | Y1 | 2+ | Y2 | 2+2 | Y1 | × | Y2 | cos2kb (3)
Точно так же, как и классическая, квантовая теория предсказывает чередующиеся усиления и ослабления частоты срабатывания детектора при плавном изменении расстояния между пластинками. Если обеспечить выполнение условия ç Y1 ç = ç Y2 ç, то при определенных расстояниях b вероятность отражения может равняться нулю, хотя амплитуды отражения и от первой и от второй пластинок не равны нулю.
|
|
|
Следующая задача является центром занятия.
Задача 4. Через две щели, ширина каждой из которых меньше длины волны амплитуды вероятности l, пропускают пучок электронов. Электроны попадают на экран, расположенный на расстоянии L от щелей. Амплитуды попадания электрона в верхнюю и в нижнюю щели одинаковы. Рассмотрите ситуацию L>>l, b, x.
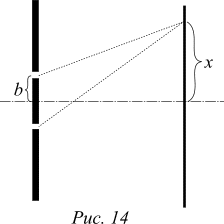 а) Полагая, что модули амплитуд вероятности электрону и из верхней и из нижней щелей попасть на экран в начало координат одинаковы и равны Y, определите частоту срабатывания детектора I, закрепленного на экране на расстоянии x от начала координат. Считайте, что частота срабатывания детектора, установленного в начале координат, равна I0. Полагайте также, что Y не зависит от x.
а) Полагая, что модули амплитуд вероятности электрону и из верхней и из нижней щелей попасть на экран в начало координат одинаковы и равны Y, определите частоту срабатывания детектора I, закрепленного на экране на расстоянии x от начала координат. Считайте, что частота срабатывания детектора, установленного в начале координат, равна I0. Полагайте также, что Y не зависит от x.
б) Получите приближенное выражение расстояния между центральным и первым максимумом интенсивности попадания электронов.
в) Дайте качественное предсказание изменения дифракционной картины в случае, когда модули амплитуд попадания электрона на экран из щелей не равны и обратно пропорциональны расстоянию от щели до места попадания.
г) Как изменится дифракционная картина, если фаза амплитуды вероятности попадания электрона в верхнюю щель меньше фазы амплитуды вероятности попадания электрона в нижнюю щель на p/6?
Решение. а) Поскольку принципиально невозможно определить, из какой щели прилетает электрон в точку x,постольку результирующая амплитуда попадания равна сумме амплитуд. Амплитуды попадания электрона из верхней и нижней щелей имеют разность фаз 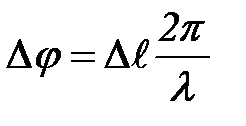 , где D l- разность хода в точку x из верхней и из нижней щелей. Она равна
, где D l- разность хода в точку x из верхней и из нижней щелей. Она равна
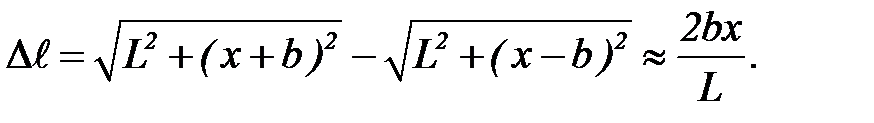 (4)
(4)
Соответствующая разность фаз при этом
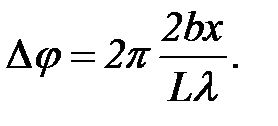 (5)
(5)
Далее складываем амплитуды по теореме косинусов, и определяем вероятность попадания электрона в точку x, как это было сделано в примере
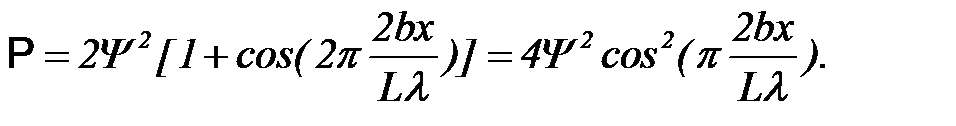 (6)
(6)
Центральный максимум находится в точке x=0. Так как интенсивность срабатывания детектора в центральном максимуме равна I0, то 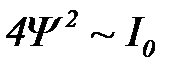 , и интенсивность срабатывания в точке x запишется в виде
, и интенсивность срабатывания в точке x запишется в виде
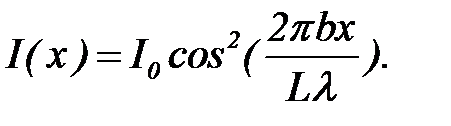 (7)
(7)
б) Расстояние между центральным и первым максимумами определится из условия
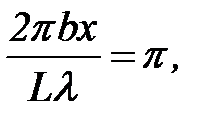 (8)
(8)
Откуда
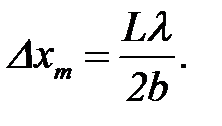 (9)
(9)
в) По мере удаления от центрального максимума при перемещении вдоль экрана будет наблюдаться различие в длинах стрелок амплитуды вероятности. В отличие от ситуации, описываемой формулой (13), которая в точках минимума дает нулевую интенсивность срабатывания детектора, вычитание волн амплитуд вероятности попадания из разных щелей не будет давать нуль. На дифракционную картину будет налагаться монотонная “подсветка”.
г) К разности фаз амплитуд вероятности, задаваемой формулой (5), добавится p/6, поэтому новая разность фаз будет равна
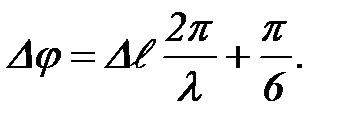 (10)
(10)
Соответственно формула (17) преобразуется к виду
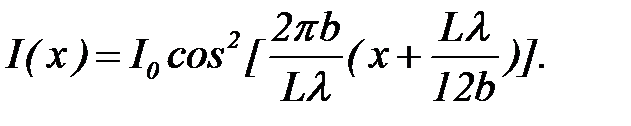 (11)
(11)
|
|
|
Формула (11) говорит, что вся дифракционная картина смещается вниз на расстояние 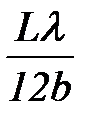 .
.
Подведем итоги решения задачи 4. При рассеянии пучка электронов на двух щелях волны амплитуды вероятности, прошедшие через верхнюю и через нижнюю щель, налагаются друг на друга (интерферируют) и возникает дифракционная картина подобная картине дифракции света на двух щелях. Замечательно, что если по очереди прикрывать ту или иную щель, то картина рассеяния не будет иметь минимумов или максимумов (так как щели очень тонкие). Максимумы и минимумы возникают только в том случае, когда открыты обе щели. Складываются амплитуды вероятности двух возможностей. Нельзя утверждать, что электрон попадает в детектор, прилетев из верхней щели или из нижней щели. Он прилетает сразу из двух щелей. Не смотря на то, что электрон является неделимой частицей, каким-то образом он пролетает сразу через две щели.
Возможность интерференции состояний является главной чертой квантовой физики. Это ее главная суть.
 2015-07-14
2015-07-14 1817
1817








