1. Задача Дирихле для уравнения Лапласа в кольце.
2. Закон больших чисел (теорема о связи 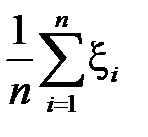 и
и 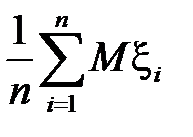 , где
, где 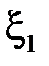 ,
, 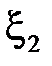 , …,
, …, 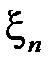 – попарно независимые величины, дисперсии которых ограничены одной и той же const) (с доказательством).
– попарно независимые величины, дисперсии которых ограничены одной и той же const) (с доказательством).
3. Решить смешанную задачу для волнового уравнения
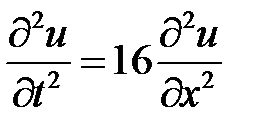 ,
, 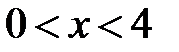 ,
,
ГУ: 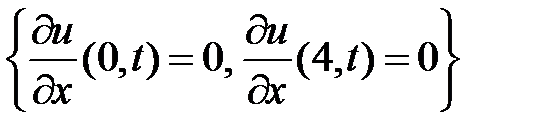 ;
;
НУ: 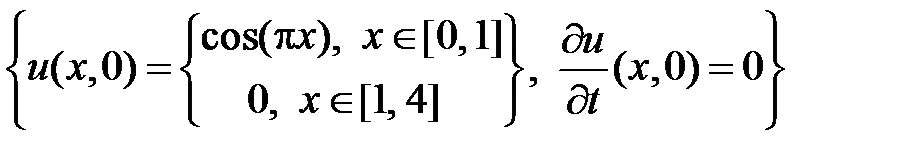 .
.
4. Найти вероятность того, что при семи подбрасываниях двух игральных кубиков пять очков в сумме появятся ровно 3 раза.
1. Уравнением Лапласа называется уравнение вида
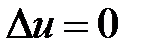 ,
,
где 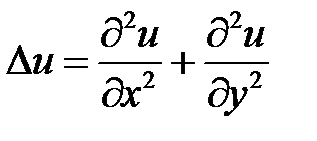 – оператор Лапласа.
– оператор Лапласа.
Задача Дирихле для уравнения Лапласа в кольце ставится следующим образом:
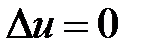 при
при 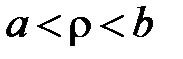 ,
,
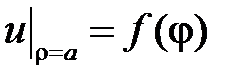 ,
, 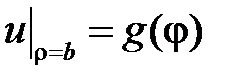 ,
,
где 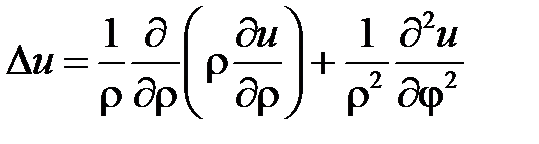 – оператор Лапласа в полярных координатах
– оператор Лапласа в полярных координатах 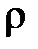 ,
, 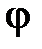 (
(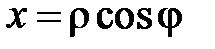 ,
, 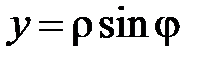 ),
), 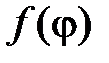 ,
, 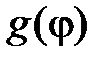 – заданные функция.
– заданные функция.
Из условия однозначности решения вытекает условие периодичности
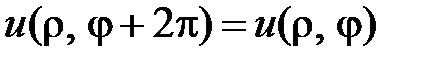 .
.
Для нахождения решения этой задачи используем метод Фурье.
Нетривиальные решения уравнения 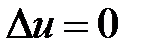 будем искать в виде
будем искать в виде
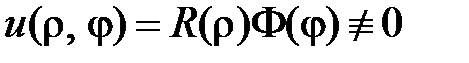 ,
,
Подставляем 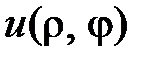 в уравнение и разделяем переменные:
в уравнение и разделяем переменные:
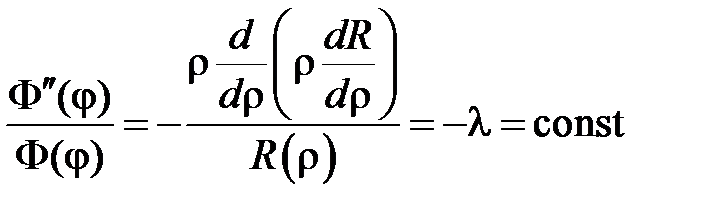 ,
,
откуда
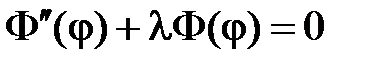 ,
,
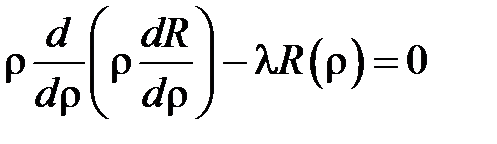 .
.
Из условия периодичности следует, что
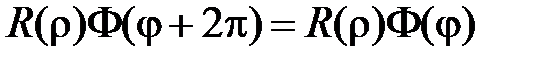 ,
, 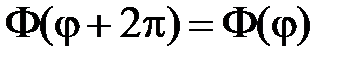 .
.
Таким образом, для  получаем задачу на собственные значения
получаем задачу на собственные значения
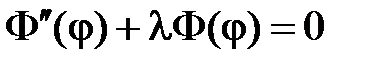 ,
,
|
|
|
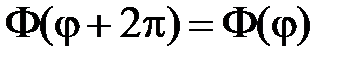 .
.
Если 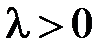 , то
, то
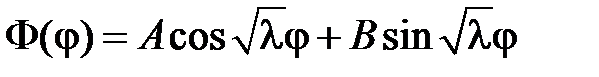 .
.
Применяем условие периодичности:
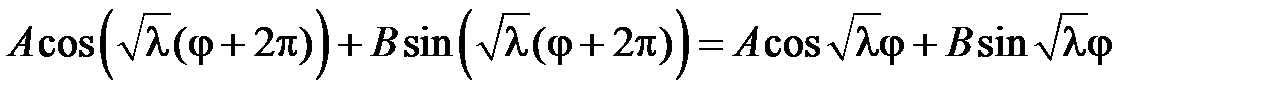 .
.
Отсюда, 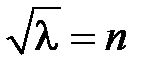 ,
, 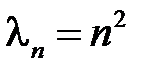 ,
, 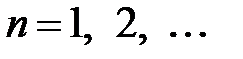 .
.
Если 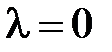 , то
, то
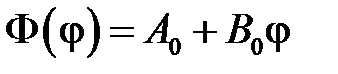 .
.
Следует взять 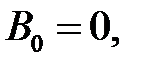 иначе не выполнится условие периодичности.
иначе не выполнится условие периодичности.
При 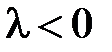 ненулевых периодических решений нет.
ненулевых периодических решений нет.
Окончательно имеем
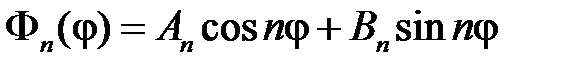 ,
, 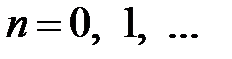 .
.
Чтобы решить уравнение для 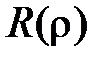 при
при 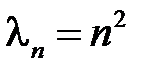 , сделаем замену
, сделаем замену 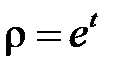 . Получим
. Получим
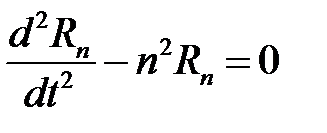 ,
, 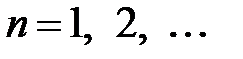 ,
,
откуда
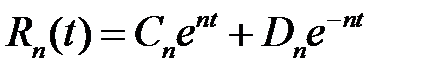 ,
,
т.е.
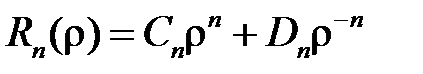 ,
, 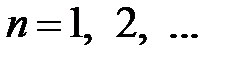 .
.
При 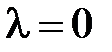 получим
получим 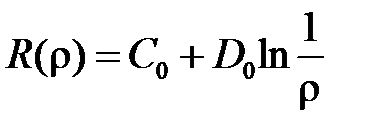 .
.
Таким образом, функции
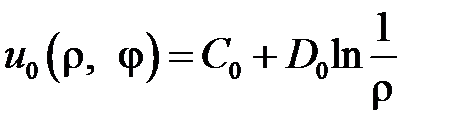 ,
,
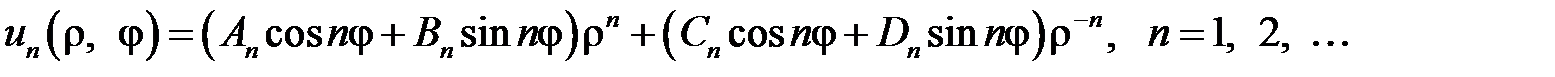
являются частными решениями уравнения 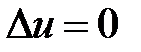 . Составим функцию
. Составим функцию
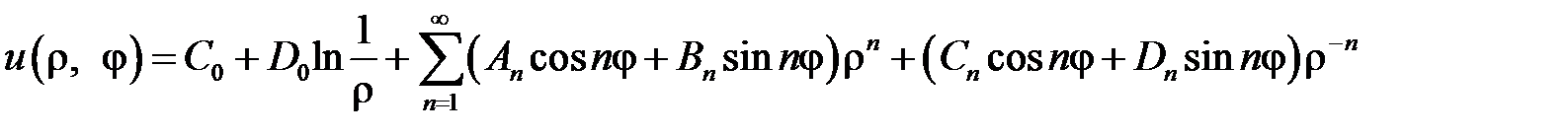 ,
,
которая вследствие линейности и однородности уравнения Лапласа также будет его решением.
Для нахождения  ,
, 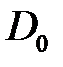 ,
, 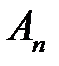 ,
, 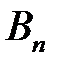 ,
, 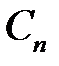 ,
, 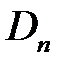 ,
, 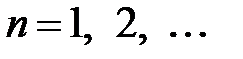 , воспользуемся краевыми условием
, воспользуемся краевыми условием 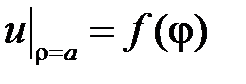 ,
, 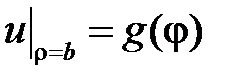 . Разложим функции
. Разложим функции 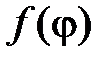 ,
, 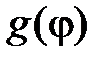 в тригонометрический ряд Фурье в промежутке
в тригонометрический ряд Фурье в промежутке 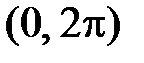 :
:
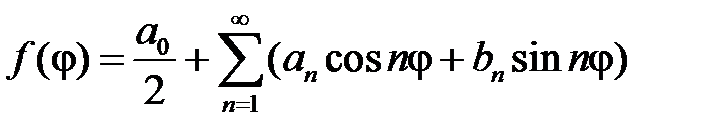 ,
,
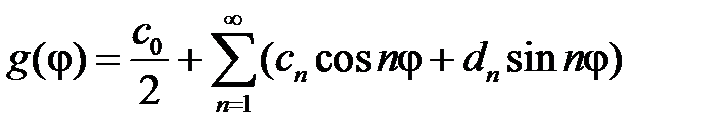 ,
,
где
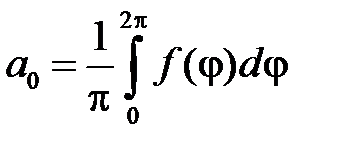 ,
, 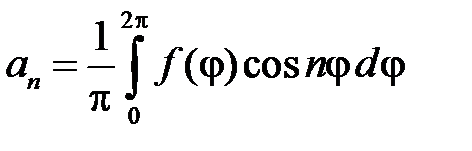 ,
, 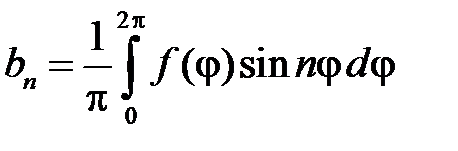 ,
, 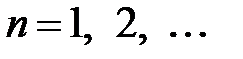 ,
,
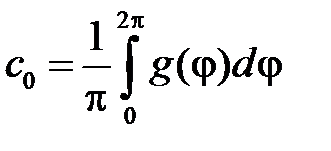 ,
, 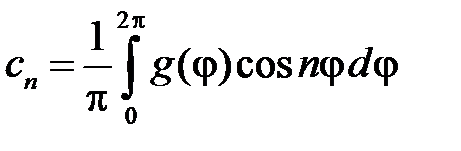 ,
, 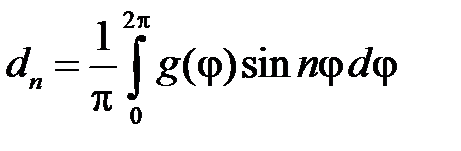 ,
, 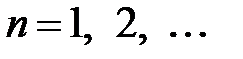 .
.
Тогда краевое условие 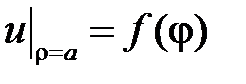 дает равенство
дает равенство
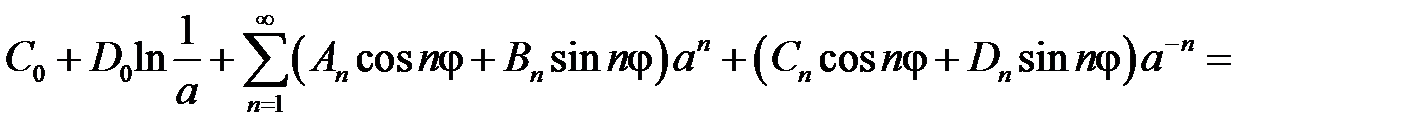
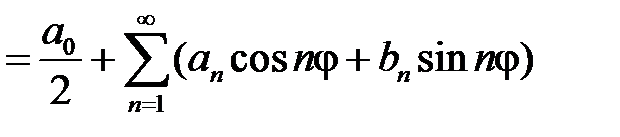 ,
,
откуда
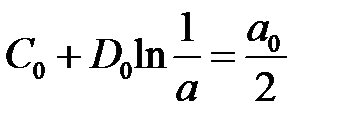 ,
, 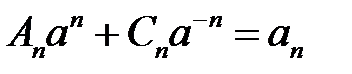 ,
, 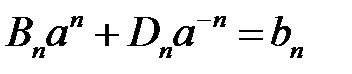 ,
, 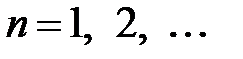 .
.
Краевое условие 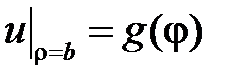 дает равенство
дает равенство
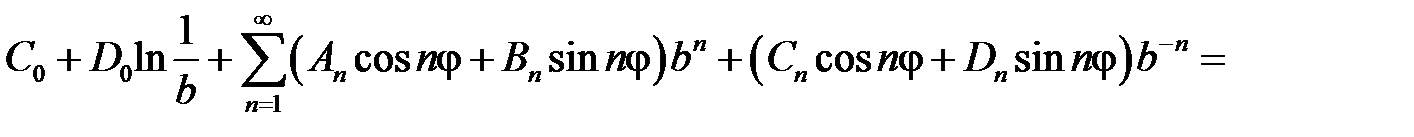
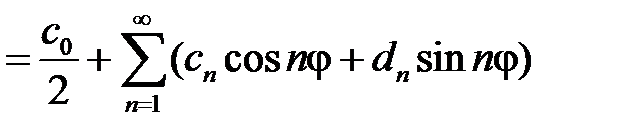 ,
,
откуда
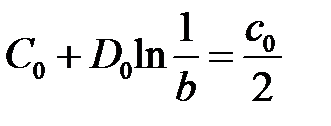 ,
, 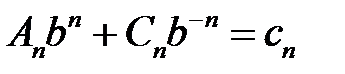 ,
, 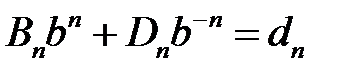 ,
, 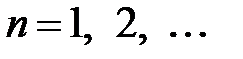 .
.
Тогда
из системы 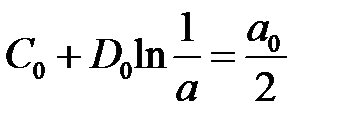 ,
, 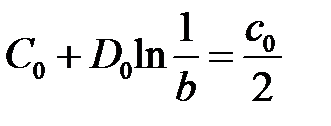 находим
находим
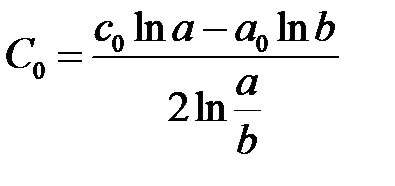 ,
, 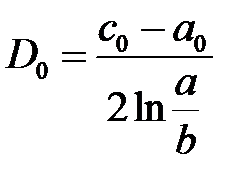 ;
;
из систем 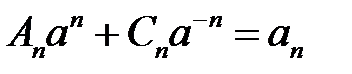 ,
, 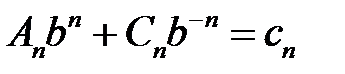 ,
, 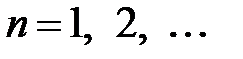 , находим
, находим
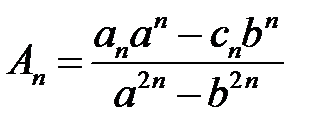 ,
, 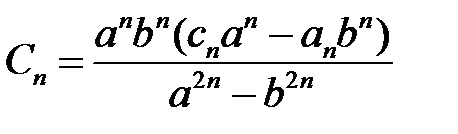 ,
, 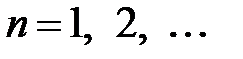 ;
;
из систем 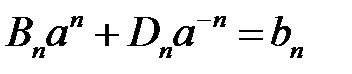 ,
, 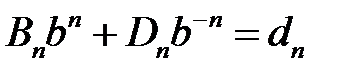 ,
, 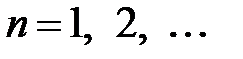 , находим
, находим
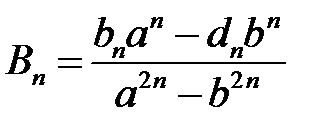 ,
, 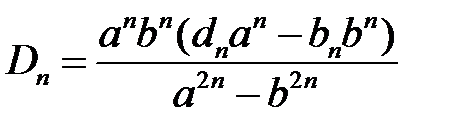 ,
, 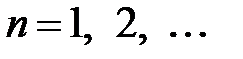 .
.
Окончательно решение задачи Дирихле для уравнения Лапласа в кольце имеет вид
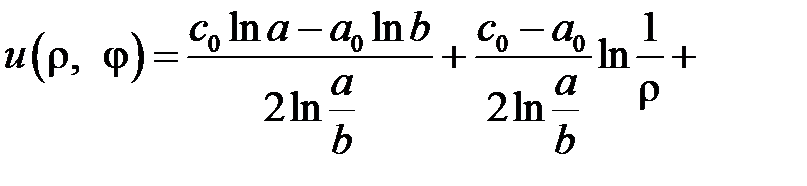
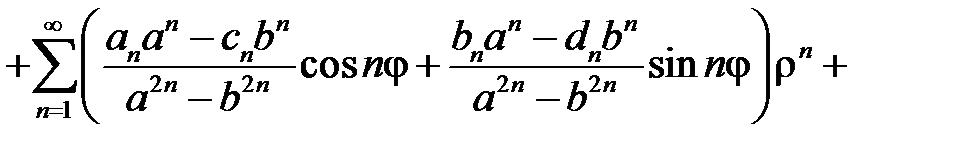
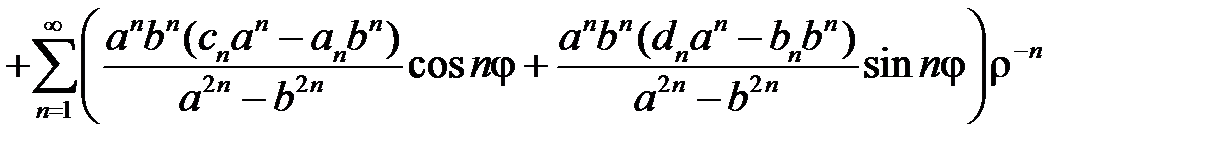 .
.
2. Пусть 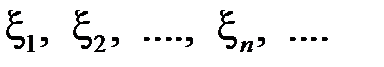 – последовательность случайных величин, для которых определены математические ожидания
– последовательность случайных величин, для которых определены математические ожидания 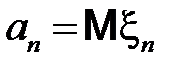 ,
, 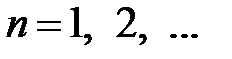 . Кроме того, пусть для любого
. Кроме того, пусть для любого 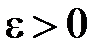
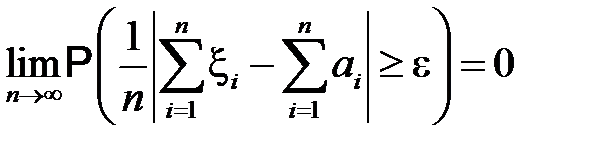 .
.
Математические теоремы, формулирующие условия такой сходимости, носят название закона больших чисел (ЗБЧ).
Рассмотрим закон больших чисел в форме Чебышева.
Введем обозначения
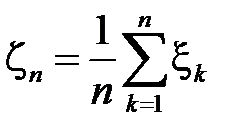 ,
, 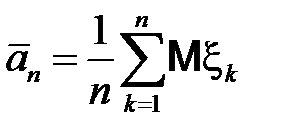 .
.
Теорема Чебышева. Пусть 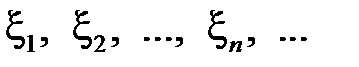 – последовательность независимых случайных величин, имеющих конечные математические ожидания
– последовательность независимых случайных величин, имеющих конечные математические ожидания 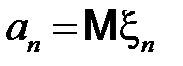 и дисперсии, ограниченные в совокупности:
и дисперсии, ограниченные в совокупности: 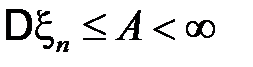 при любом
при любом 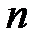 . Тогда для любого
. Тогда для любого 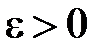
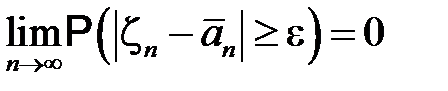 .
.
Доказательство. Поскольку случайные величины 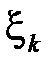 независимы, то
независимы, то
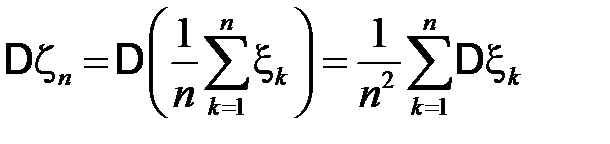 ,
,
Кроме того,
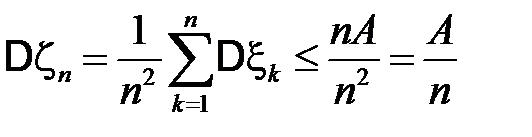 ,
,
поскольку дисперсии 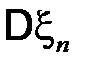 ограничены в совокупности.
ограничены в совокупности.
Применим к вероятности 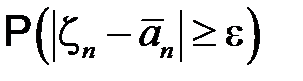 неравенство Чебышева и неравенство для
неравенство Чебышева и неравенство для 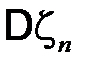 :
:
|
|
|
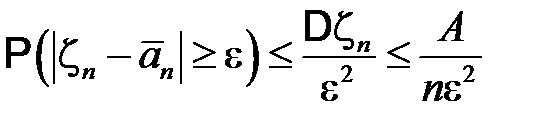 .
.
Последнее при любом 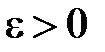 стремится к нулю при
стремится к нулю при 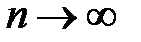 . Теорема доказана.
. Теорема доказана.
3. Для решения задачи воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 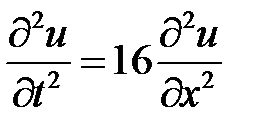 будем искать в виде
будем искать в виде 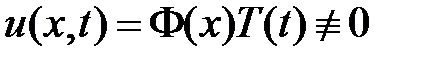 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
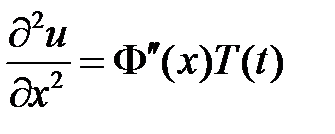 ,
, 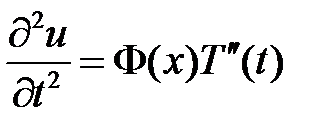 ,
,
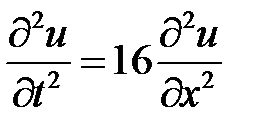 :
: 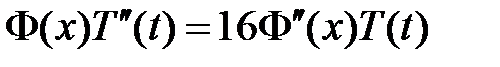 ,
,
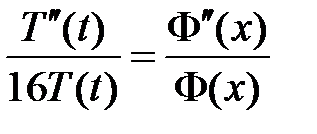 ,
, 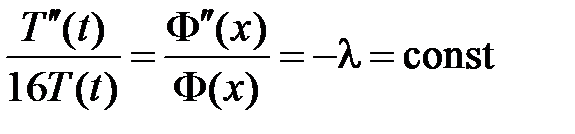 ,
, 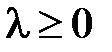 .
.
Тогда функции 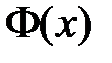 и
и 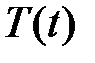 являются соответственно решениями уравнений
являются соответственно решениями уравнений
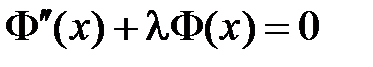 ,
, 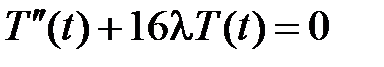 .
.
Из граничных условий 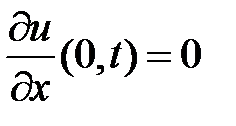 ,
, 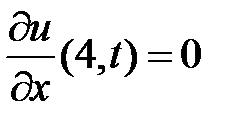 получаем краевые условия для функции
получаем краевые условия для функции 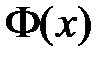 :
: 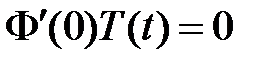 ,
, 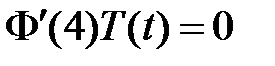 , значит,
, значит, 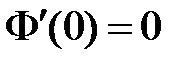 ,
, 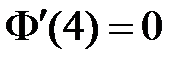 . Таким образом, для определения
. Таким образом, для определения 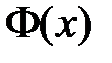 и
и 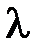 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
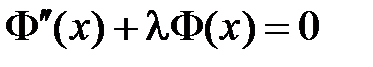
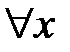 :
: 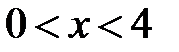 ,
,
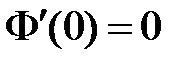 ,
, 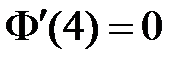 .
.
Поскольку мы имеем дело со второй краевой задачей, то 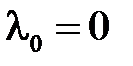 является собственным значением, а
является собственным значением, а 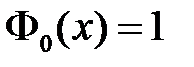 – соответствующей ему собственной функцией.
– соответствующей ему собственной функцией.
Пусть теперь 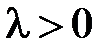 (при
(при 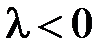 задача имеет только тривиальные решения). Общее решение уравнения
задача имеет только тривиальные решения). Общее решение уравнения 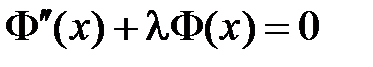 имеет вид
имеет вид
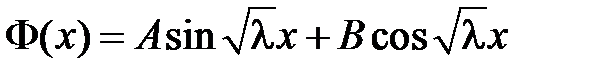 .
.
Тогда 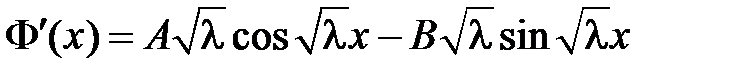 . Из краевого условия
. Из краевого условия 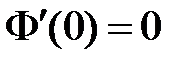 получаем:
получаем: 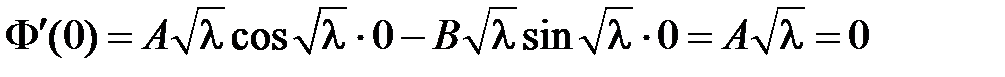 ,
, 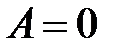 , т.е.
, т.е. 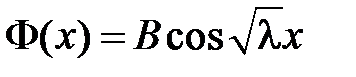 и
и 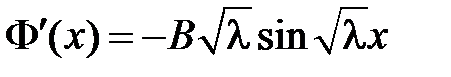 .
.
Из краевого условия 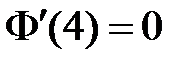 получаем:
получаем: 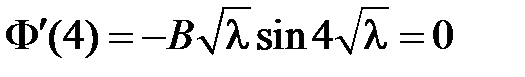 . Поскольку
. Поскольку 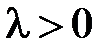 и
и 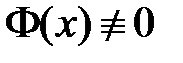 , то
, то 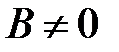 и равенство
и равенство 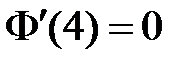 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 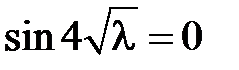 , откуда получаем
, откуда получаем 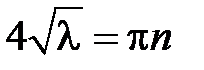 ,
, 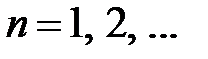 , т.е.
, т.е. 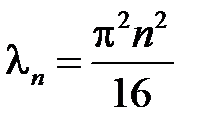 ,
, 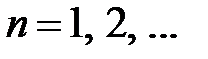 . Тогда получим
. Тогда получим 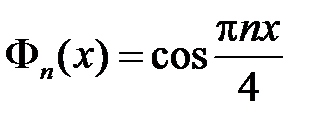 ,
, 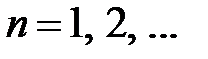 . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 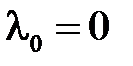 ,
, 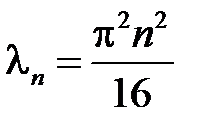 ,
, 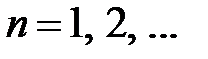 ;
;
собственные функции 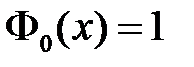 ,
, 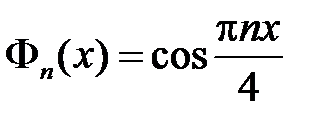 ,
, 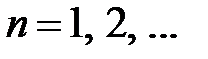 .
.
Теперь при каждом 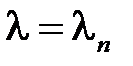 решаем уравнение для
решаем уравнение для 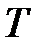 :
:
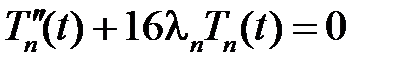 ,
, 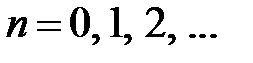 .
.
При 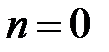 получим уравнение
получим уравнение 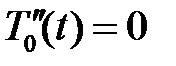 , откуда
, откуда
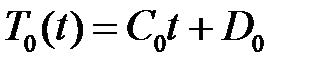 .
.
При 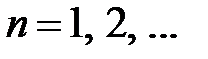 общее решение этого уравнения имеет вид
общее решение этого уравнения имеет вид
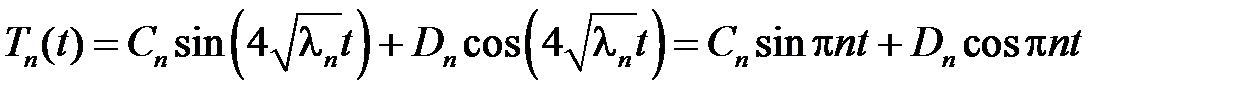 .
.
Тогда
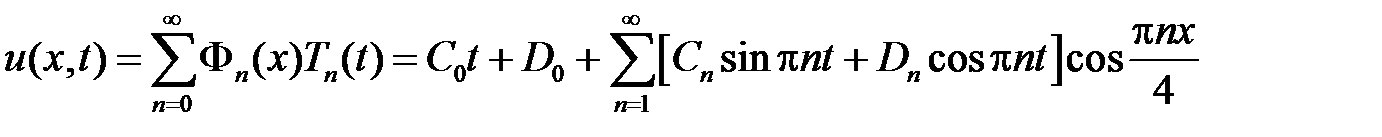 .
.
Для нахождения коэффициентов 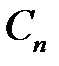 ,
, 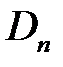 ,
, 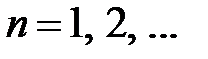 , воспользуемся начальными условиями
, воспользуемся начальными условиями 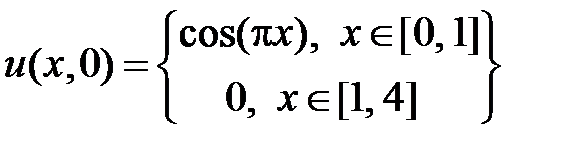 ,
, 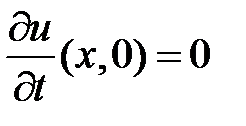 .
.
Разложим функцию 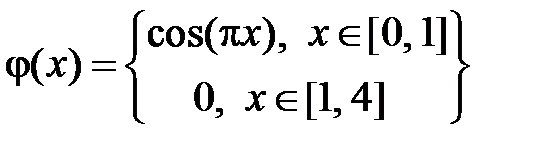 на отрезке
на отрезке  в ряд Фурье по системе
в ряд Фурье по системе  :
:
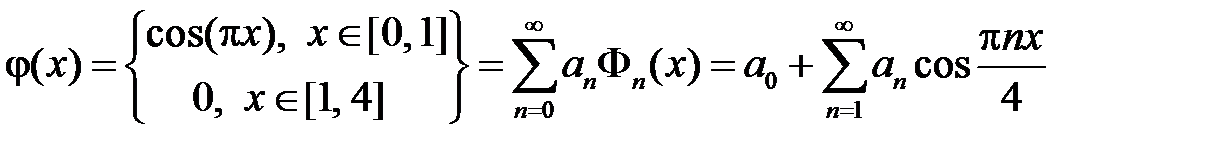 ,
,
где
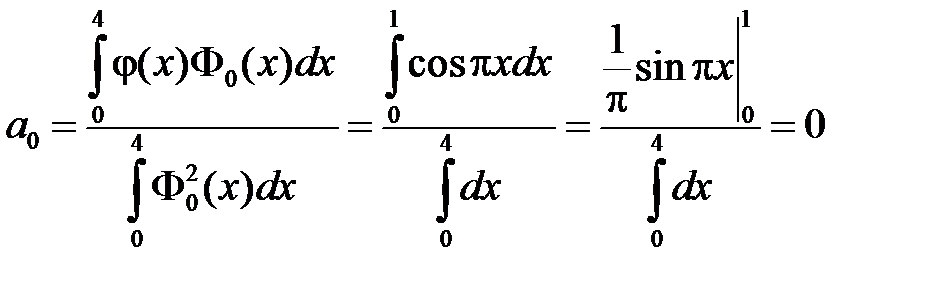 ,
,
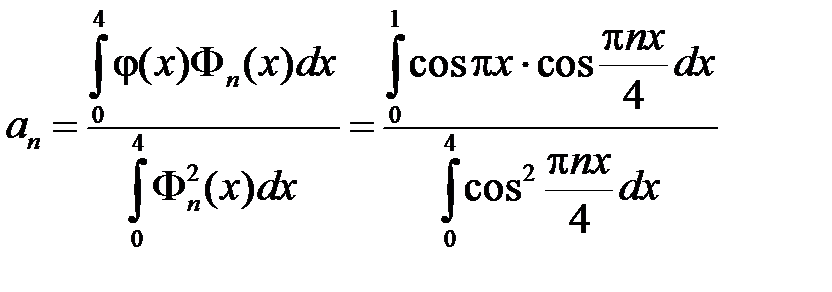 .
.
Находим
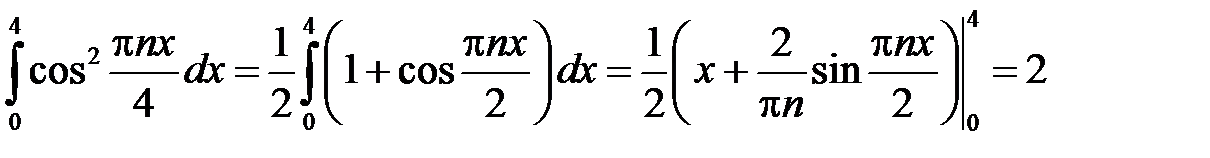 ,
,
при 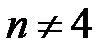
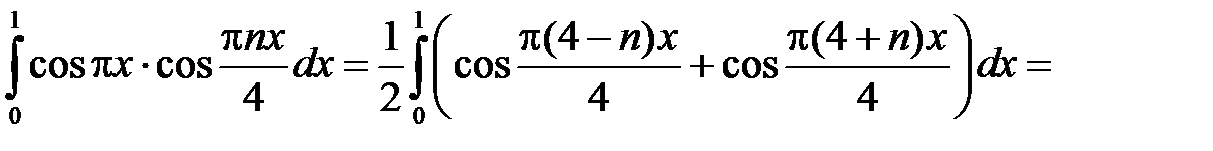
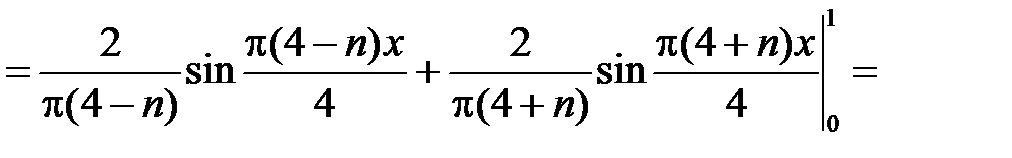
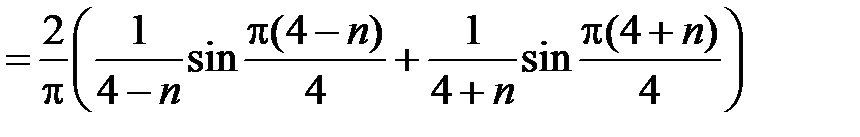 ,
,
при 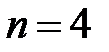
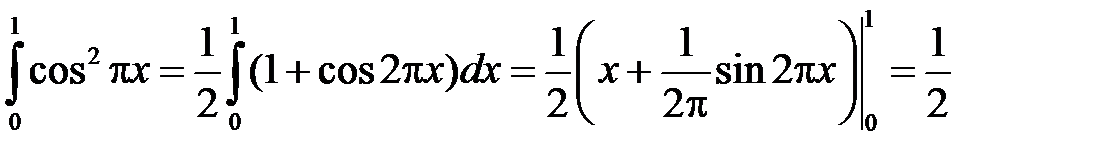 .
.
Итак,
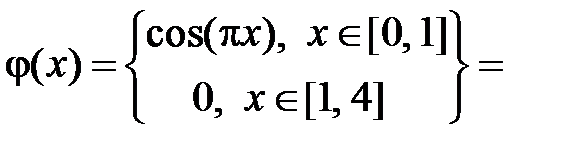
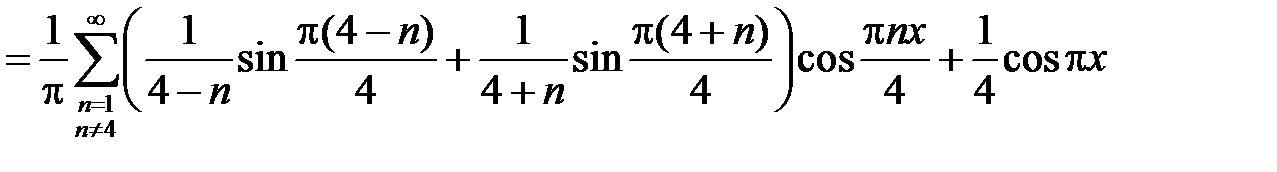 .
.
Тогда начальное условие 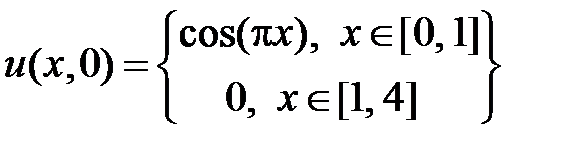 дает
дает
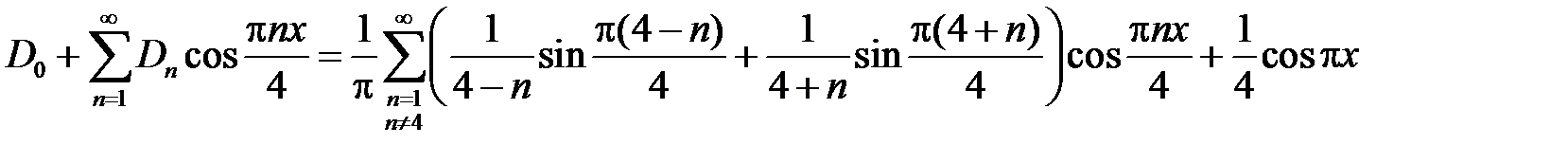 ,
,
откуда
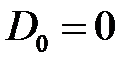 ,
, 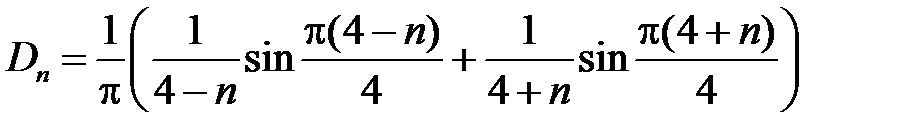 ,
, 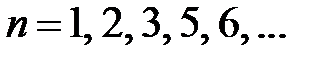 ,
, 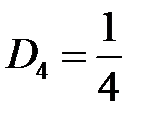 .
.
Находим 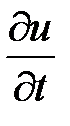 :
:
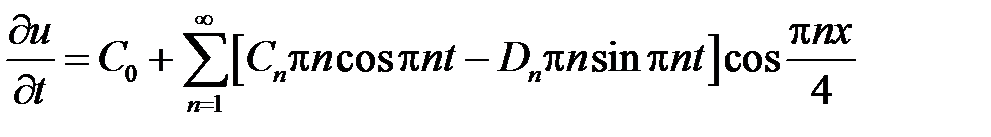 .
.
Тогда начальное условие 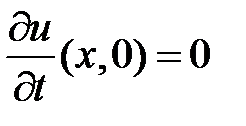 дает
дает
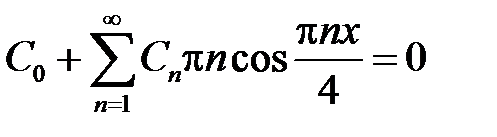 ,
,
откуда
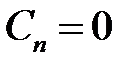 ,
, 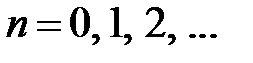 .
.
Тогда решение задачи есть ряд
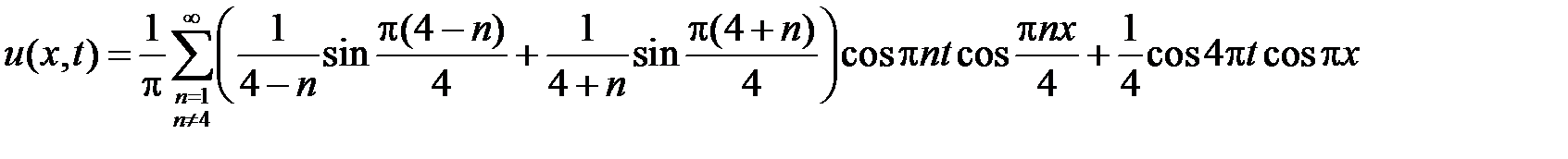 .
.
4. Мы имеем дело с последовательностью независимых испытаний по схеме Бернулли, где событие «успех» – выпадение при подбрасывании двух игральных кубиков в сумме пяти очков. Поскольку при подбрасывании двух игральных кубиков всего возможно 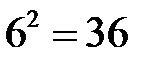 исходов, а сумме 5 может появиться четырьмя способами:
исходов, а сумме 5 может появиться четырьмя способами: 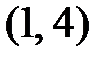 ,
, 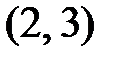 ,
, 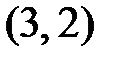 ,
, 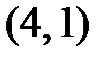 , то вероятность «успеха» равна
, то вероятность «успеха» равна 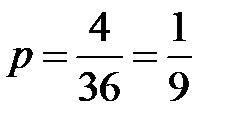 . Проведено
. Проведено 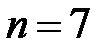 испытаний. Тогда по формуле Бернулли вероятность того, что «успех» появится ровно 3 раза (т.е. при семи подбрасываниях двух игральных кубиков пять очков в сумме появятся ровно 3 раза), равна
испытаний. Тогда по формуле Бернулли вероятность того, что «успех» появится ровно 3 раза (т.е. при семи подбрасываниях двух игральных кубиков пять очков в сумме появятся ровно 3 раза), равна
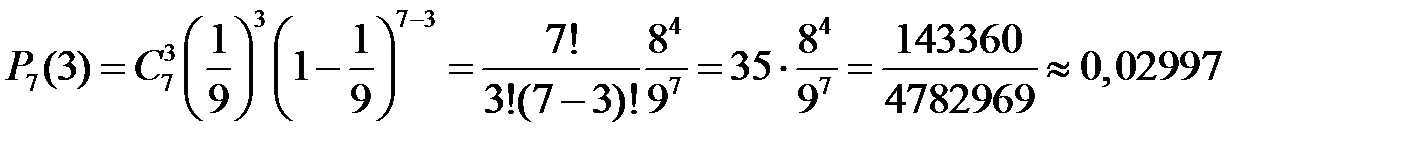 .
.
 2015-07-14
2015-07-14 385
385