Для линейной стохастической функции регрессии характерно то, что ее регрессоры (независимые переменные) не случайные (детерминированные) величины. Однако эта предпосылка не выполняется для многих прикладных моделей, поэтому в группу регрессоров включают стохастические величины и рассматривают обобщенные классические модели. При этом объект исследования представляют регрессионной функцией:
Y = f(x) + U
При изучении связей экономических показателей производства (деятельности) используют различного вида уравнения линейной и нелинейной связи (регрессии).
Нелинейные регрессии делятся на два класса: нелинейные относительно переменных ( но линейные по оцениваемымпараметрам) – полиномы разных степеней,гипербола и другие функции; и нелинейные по оцениваемым параметрам – степенная, показательная, экспоненциальная и др. Внимание к линейным регрессиям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи с помощью простых преобразований, например логарифмирования или замены переменных, можно привести к линейной форме. При этом необходимо чтобы нормальный закон распределения в моделях имел, например, логарифм вектора возмущений, а не вектор как в случае линейной формы связи. Построение уравнения регрессии сводится к оценке ее параметров.
Относительно отклонений 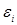 = Y - Ŷ сделаем следующие предпосылки:
= Y - Ŷ сделаем следующие предпосылки:
1) величина 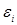 является случайной переменной;
является случайной переменной;
2) математическое ожидание 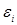 равно нулю;
равно нулю;
3) дисперсия 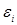 постоянна:
постоянна: 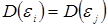 для всех i и j;
для всех i и j;
4) значения 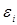 независимы между собой.
независимы между собой.
Эконометрическая модель с двумя переменными (простая модель) имеет вид:
Ŷ = a0 + a1x + ε, (3.1)
где ε - случайная (стохастическая) составляющая. Предположим, что стохастическая составляющая нормально распределенная, имеет нулевое математическое ожидание и постоянную дисперсию. Тогда уравнение регрессии примет вид:
Ŷ = a0 + a1x
Для оценки параметров уравнения используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака (регрессанда) Y от теоретических Ŷ минимальна.
Для линейных и нелинейных уравнений, приводимых к линейным, составляется и решается следующая система нормальных уравнений относительно параметров регрессии а0 и а1:
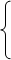 na0 + Σxi.a1 = Σyi
na0 + Σxi.a1 = Σyi
Σxi.a0 + Σxi²a1 = Σ xiyi (3.2)
Можно, так же, использовать формулы, которые следуют из этой системы:






 а0 = y - а1. x; а1 = (x.y - x. y)/ (x2) - (x)2) (3. 3)
а0 = y - а1. x; а1 = (x.y - x. y)/ (x2) - (x)2) (3. 3)
Определив значения а0 и а1 и подставив их в уравнение связи найдем Ŷ.
Известно, что если приведенные выше условия относительно отклонений 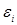 выполняются, то оценки а и b, полученные с помощью метода наименьших квадратов, обладают следующими свойствами:
выполняются, то оценки а и b, полученные с помощью метода наименьших квадратов, обладают следующими свойствами:
1. Оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению: М(а) = 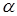 ; М(b) =
; М(b) = 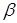 . Это вытекает из того, что М(
. Это вытекает из того, что М(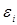 ) = 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.
) = 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.
2. Оценки состоятельны, т. к. дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю:
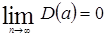 ;
; 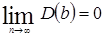
Иначе говоря, надежность оценки при увеличении выборки растет.
3. Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра.
Перечисленные свойства не зависят от конкретного вида распределения величин 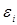 тем не менее обычно предполагается, что они распределены нормально. Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов.
тем не менее обычно предполагается, что они распределены нормально. Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов.
Если предположения 3) и 4) нарушены, т. е. дисперсия возмущений непостоянна или значения 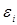 связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойства эффективности - нет.
связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойства эффективности - нет.
К получению параметров модели:
Рассмотрим случай, когда имеется п наблюдений двух переменных х и у. Предположив, что у зависит от х, и необходимо подобрать уравнение
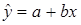 (1.1)
(1.1)
Расчетное значение зависимой переменной 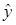 и отклонения
и отклонения 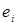 для наблюдения i определяются уравнениями:
для наблюдения i определяются уравнениями:
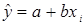
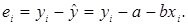
Сумма квадратов отклонений равна:
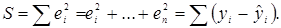
Тогда требование наименьших квадратов записывается в виде:
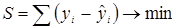 , (1.2)
, (1.2)
т. е. сумма квадратов отклонений фактических ординат точек корреляционного поля от ординат, вычисленных по уравнению (1.1), должна быть наименьшей.
Метод нахождения параметров прямой, удовлетворяющей этому требованию, называется одношаговым методом наименьших квадратов(1-МНК).
Для парной линейной регрессии задача заключается в нахождении неизвестных параметров а и b, минимизирующих сумму квадратов отклонений, т. е. функцию S:
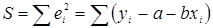
Значения а и b, удовлетворяющие минимуму функции S, находят из уравнений:
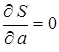 ,
, 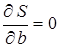
Выразим квадрат i-го остатка:
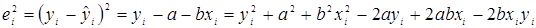 .
.
Суммируя по всем n наблюдениям, запишем S в виде:
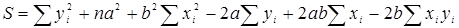
Тогда условия минимизации функции S принимают вид:
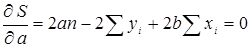
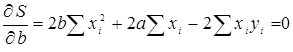
Подставив в первое уравнение 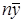 вместо
вместо 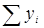 и
и 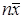 вместо
вместо 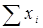 , получим:
, получим:
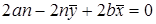
Следовательно,
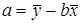
Подставив полученное выражение для а во второе уравнение минимизации, имеем:
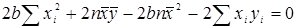
После преобразования получим:
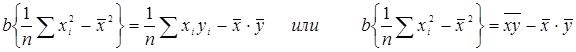
Откуда
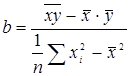 или
или 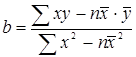
Так как показатель ковариации равен:
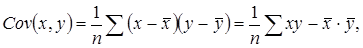
а дисперсия равна:
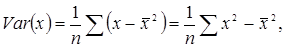
то параметр b можно выразить как:
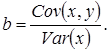
Коэффициент корреляции определяется по формуле:
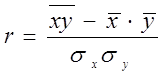
где 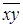 - среднее значение произведений х и у;
- среднее значение произведений х и у; 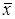 ,
, 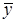 - средние значения соответствующих признаков;
- средние значения соответствующих признаков; 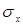 и
и 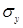 - среднеквадратические отклонения, найденные по признаку х и по признаку у.
- среднеквадратические отклонения, найденные по признаку х и по признаку у.
Коэффициент корреляции можно также установить через показатель ковариации:
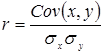
Зная значения 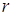 ,
, 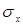 ,
, 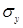 , можно вычислить коэффициенты корреляционного уравнения по следующим формулам:
, можно вычислить коэффициенты корреляционного уравнения по следующим формулам:
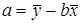
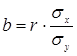 .
.
 2015-07-14
2015-07-14 354
354








