Комплексная цель модуля: освоение конечно-разностных методов решения задач математической физики.
Содержание модуля: понятия аппроксимации, сходимости, устойчивости; явная и неявная схемы метода конечных разностей решения задач для уравнений гиперболического и параболического типов.
§ 16. Вычислительные методы решения краевых задач математической физики.
16.1. Разностные схемы для уравнений с частными производными. Основные понятия. Рассмотрим некоторые основные способы построения разностных схем и проверки их устойчивости примерами разностных схем для уравнений с частными производными. При изложении будем следовать [21].
Определение сходимости. Пусть требуется приближенно вычислить решение 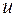 дифференциальной краевой задачи
дифференциальной краевой задачи
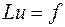 , ,
| (16.1) |
поставленной в некоторой области 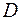 с границей
с границей 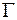 . Для этого следует выбрать дискретное множество точек
. Для этого следует выбрать дискретное множество точек 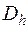 - сетку, - принадлежащее
- сетку, - принадлежащее 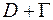 , ввести линейное нормированное пространство
, ввести линейное нормированное пространство 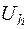 функций, определенных на сетке
функций, определенных на сетке 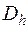 , установить соответствие между решением
, установить соответствие между решением 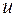 и функцией
и функцией 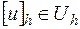 , которую будем считать искомой таблицей решения
, которую будем считать искомой таблицей решения 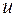 . Для приближенного отыскания таблицы
. Для приближенного отыскания таблицы 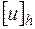 , которую мы условились считать точным решением задачи (16.1), надо на основе задачи (16.1) составить такую систему уравнений
, которую мы условились считать точным решением задачи (16.1), надо на основе задачи (16.1) составить такую систему уравнений
|
|
|
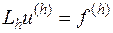
| (16.2) |
относительно функции 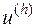 из
из 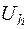 , чтобы имела место сходимость
, чтобы имела место сходимость
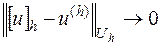 при при 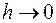 . .
| (16.3) |
Если для решения разностной краевой задачи (16.2) выполнено неравенство
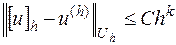
то говорят, что сходимость имеет порядок 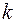 относительно
относительно 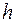 .
.
Задачу построения сходящейся разностной схемы (16.2) разбивают на две – на построение разностной схемы (16.2), аппроксимирующей задачу (16.1) на решении 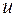 последней, и на проверку устойчивости схемы (16.2).
последней, и на проверку устойчивости схемы (16.2).
Определение аппроксимации. Чтобы это понятие имело смысл, надо ввести норму в пространстве 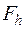 , которому принадлежит правая часть
, которому принадлежит правая часть 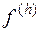 уравнения (16.2). По определению, разностная задача (16.2) аппроксимирует задачу (16.1) на решении
уравнения (16.2). По определению, разностная задача (16.2) аппроксимирует задачу (16.1) на решении 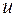 , если в равенстве
, если в равенстве
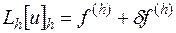
невязка 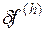 , возникающая при подстановке
, возникающая при подстановке 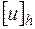 в разностную краевую задачу (16/2), стремится к нулю при
в разностную краевую задачу (16/2), стремится к нулю при 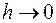 :
:
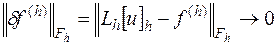 .
.
Если
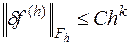 ,
,
где 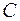 не зависит от
не зависит от 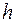 , то аппроксимация имеет порядок
, то аппроксимация имеет порядок 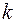 относительно
относительно 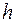 .
.
Построим, например, для задачи Коши
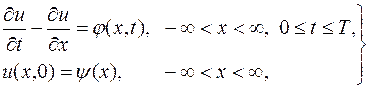
| (16.4) |
одну из аппроксимирующих ее разностных схем. Задача (16.4) записывается в форме (16.1), если положить
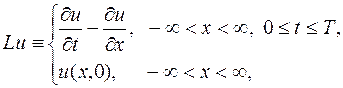
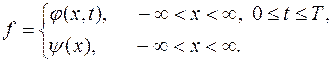
В качестве сетки 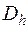 (рис. 16.1) используем совокупность точек пересечения прямых
(рис. 16.1) используем совокупность точек пересечения прямых
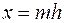 ,
, 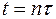 ,
, 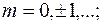
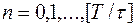 ,
,
где 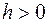 ,
, 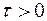 - некоторые числа, a
- некоторые числа, a 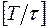 - целая часть дроби
- целая часть дроби 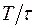 . Будем считать, что шаг
. Будем считать, что шаг 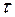 связан с шагом
связан с шагом 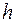 зависимостью
зависимостью 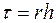 , где
, где 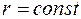 , так что сетка
, так что сетка 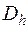 зависит только от одного параметра
зависит только от одного параметра 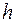 . Искомой сеточной функцией является таблица
. Искомой сеточной функцией является таблица 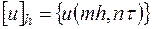 значений решения
значений решения 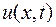 задачи (16.4) в точках сетки
задачи (16.4) в точках сетки 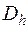 .
.
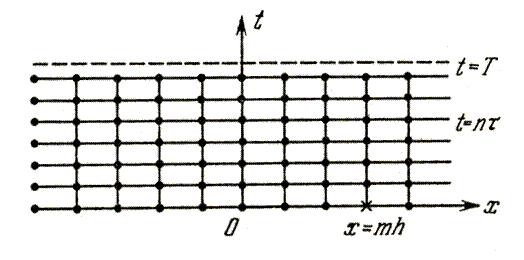
Рис. 16.1
Перейдем к построению аппроксимирующей задачу (16.4) разностной схемы (16.2). Значения сеточной функции 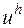 в точках
в точках 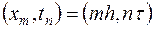 сетки
сетки 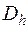 будем обозначать
будем обозначать 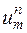 . Схему (16.2) получим, приблизив производные
. Схему (16.2) получим, приблизив производные 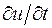 и
и 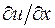 разностными отношениями
разностными отношениями
|
|
|
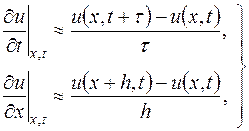
| (16.4′) |
Эта схема имеет вид
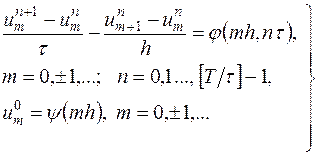
| (16.5) |
Оператор 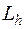 и правая часть
и правая часть 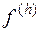 для схемы (16.5) задаются соответственно равенствами
для схемы (16.5) задаются соответственно равенствами
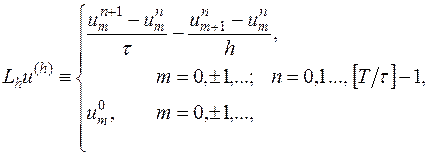
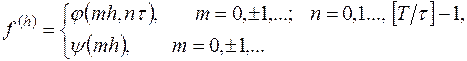
Таким образом, 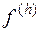 - это пара сеточных функций
- это пара сеточных функций 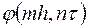 и
и 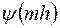 , одна из которых задана на двумерной сетке
, одна из которых задана на двумерной сетке
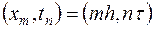 ,
, 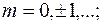
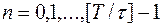 ,
,
(см. рис. 16.1), а другая – на одномерной
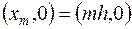 ,
, 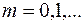
Разностное уравнение (16.5) можно разрешить относительно 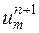 , получив
, получив
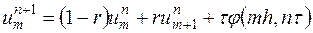
| (6) |
Итак, зная значения 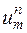 ,
, 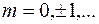 , решения
, решения  в точках сетки при
в точках сетки при 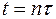 , можно вычислить значения
, можно вычислить значения 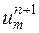 в точках сетки при
в точках сетки при 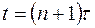 . Поскольку значения
. Поскольку значения 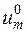 при
при 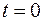 заданы равенствами
заданы равенствами 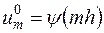 , мы можем шаг за шагом вычислить значения решения
, мы можем шаг за шагом вычислить значения решения 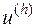 в точках сетки на прямых
в точках сетки на прямых 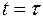 ,
, 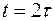 и т.д., т.е. всюду на
и т.д., т.е. всюду на  .
.
Перейдем к выяснению порядка аппроксимации, которым обладает схема (16.5). За  можно принять линейное пространство всех пар ограниченных функций
можно принять линейное пространство всех пар ограниченных функций 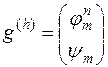 , положив
, положив
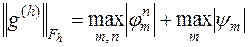
Норма, в которой рассматривается аппроксимация, может быть выбрана многими способами и выбор этот небезразличен. Пока нам будет достаточно в качестве нормы брать верхнюю грань модулей всех компонент, образующих элемент 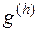 пространства
пространства 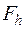 . Будем иметь в виду всюду в этом параграфе именно такую норму.
. Будем иметь в виду всюду в этом параграфе именно такую норму.
Предположим, что решение 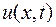 задачи (16.4) имеет ограниченные вторые производные. Тогда по формуле Тейлора
задачи (16.4) имеет ограниченные вторые производные. Тогда по формуле Тейлора
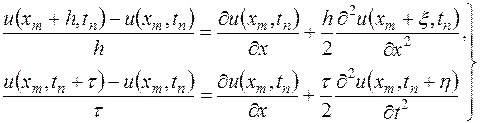
| (16.7) |
где 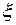 и
и 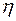 - некоторые числа, зависящие от
- некоторые числа, зависящие от 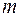 ,
, 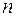 и
и 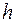 и удовлетворяющие неравенствам
и удовлетворяющие неравенствам 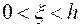 ,
, 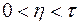 .
.
С помощью формул (16.7) выражение
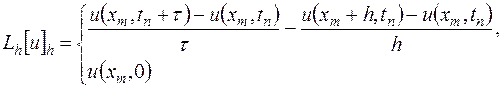
можно записать в виде
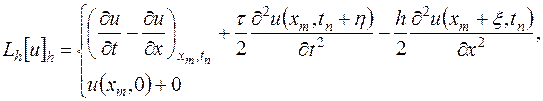

или
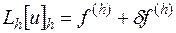 ,
,
где
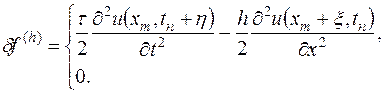
Следовательно,
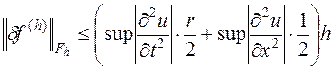 .
.
Таким образом, рассматриваемая разностная схема (16.5) имеет первый порядок аппроксимации относительно 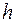 на решении
на решении 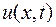 , обладающем ограниченными вторыми производными.
, обладающем ограниченными вторыми производными.
Определение устойчивости. Дадим и проиллюстрируем теперь определение устойчивости. Разностная краевая задача (16.2), по определению, устойчива, если существуют числа 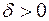 и
и 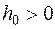 такие, что при любом
такие, что при любом 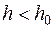 и любом
и любом 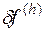 из
из 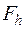 , удовлетворяющее неравенству
, удовлетворяющее неравенству 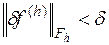 , разностная краевая задача
, разностная краевая задача
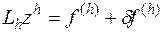
имеет одно и только одно решение, причем выполняется условие
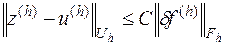 ,
,
где 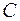 - некоторая постоянная, не зависящая от
- некоторая постоянная, не зависящая от 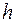 .
.
Можно показать, что в случае линейного оператора 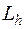 сформулированное определение равносильно следующему.
сформулированное определение равносильно следующему.
Определение. Разностная краевая задача (16.2) устойчива, если существует 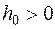 такое, что при
такое, что при 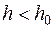 и любом
и любом 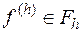 она однозначно разрешима, причем
она однозначно разрешима, причем
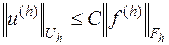
| (16.8) |
где 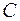 - некоторая постоянная, не зависящая от
- некоторая постоянная, не зависящая от 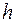 и от
и от 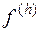 .
.
Свойство устойчивости можно трактовать как равномерную относительно 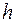 чувствительность решения разностной краевой задачи (16.2) к возмущению
чувствительность решения разностной краевой задачи (16.2) к возмущению 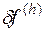 правой части.
правой части.
Подчеркнем, что в силу приведенного определения устойчивость есть некоторое внутреннее свойство разностной краевой задачи. Оно формулируется независимо от какой-либо связи с дифференциальной краевой задачей, в частности независимо от аппроксимации или сходимости.
Сформулируем без доказательства важную теорему: если разностная краевая задача аппроксимирует на решении и дифференциальную и устойчива, то имеет место сходимость (16.3). При этом порядок относительно 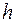 скорости сходимости совпадает с порядком аппроксимации.
скорости сходимости совпадает с порядком аппроксимации.
Покажем, что разностная схема (16.5) при 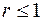 устойчива. При этом норму
устойчива. При этом норму 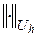 определим равенством
определим равенством
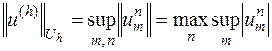 .
.
Норму 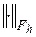 будем понимать, как выше: если
будем понимать, как выше: если 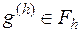 ,
,
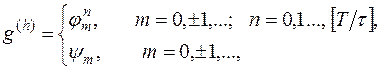
то
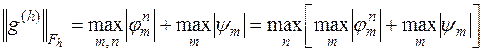 .
.
Разностную задачу
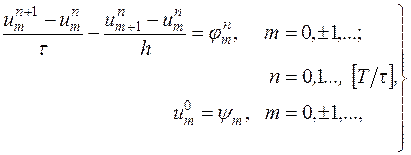
| (16.5′) |
которая отличается от задачи (16.5) только тем, что 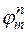 и
и 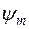 - произвольные правые части, вообще говоря, не совпадающие с
- произвольные правые части, вообще говоря, не совпадающие с 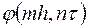 и
и 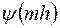 , перепишем в форме
, перепишем в форме
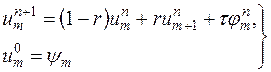
| (16.6′) |
Поскольку 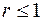 , то
, то 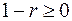 . В этом случае справедлива оценка
. В этом случае справедлива оценка
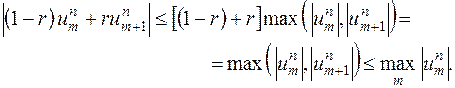
Используя эту оценку, выводим из (16.6′) неравенство
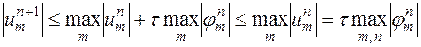
| (16.6′′) |
Отметим, что в случае 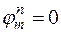 из неравенства (16.6′′) следует, что
из неравенства (16.6′′) следует, что 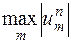 не возрастает с ростом
не возрастает с ростом 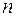 . Отмеченное свойство разностной схемы принято называть принципом максимума. Для краткости будем иногда пользоваться этим названием для всего неравенства
. Отмеченное свойство разностной схемы принято называть принципом максимума. Для краткости будем иногда пользоваться этим названием для всего неравенства
|
|
|
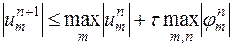 .
.
Правая часть этого неравенства не зависит от 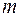 , так что в левой части вместо
, так что в левой части вместо 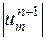 можно написать
можно написать 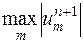 , получив неравенство
, получив неравенство
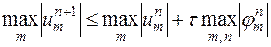 .
.
Аналогично получаем неравенства
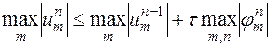 ,
,
...................,
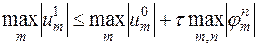
После почленного сложения этих неравенств и приведения подобных членов получим
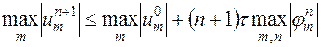 .
.
Отсюда непосредственно следует
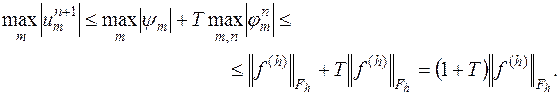
Доказанное неравенство
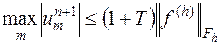
имеет место для всех  , так что оно остается справедливым, если вместо
, так что оно остается справедливым, если вместо  написать
написать 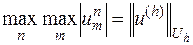 :
:
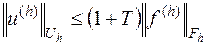 . .
| (16.9) |
Неравенство (16.9) означает устойчивость линейной задачи (16.5), поскольку существование и единственность решения задачи (16.6′) при произвольных ограниченных  и
и  , очевидно, имеют место. Роль постоянной
, очевидно, имеют место. Роль постоянной 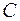 в неравенстве (16.8) играет здесь число
в неравенстве (16.8) играет здесь число 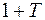 .
.
Не следует думать, что одна только аппроксимация дифференциальной краевой задачи (16.1) разностной краевой задачей обеспечивает устойчивость и, следовательно, сходимость (16.3).
В случае уравнений с частными производными непригодность наудачу взятой аппроксимирующей разностной схемы является правилом, а выбор устойчивой (и, следовательно, сходящейся) разностной схемы – постоянной заботой вычислителя.
Напомним, например, что доказательство устойчивости разностной схемы (16.5) мы провели в предположении, что 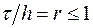 . В случае
. В случае 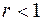 разностная задача (16.5) по-прежнему аппроксимирует задачу (16.4), но наше доказательство устойчивости не проходит.
разностная задача (16.5) по-прежнему аппроксимирует задачу (16.4), но наше доказательство устойчивости не проходит.
16.2. Вычислительная практика
Целью настоящей работы является освоение техники решения уравнений гиперболического и параболического типов при помощи явной и неявной схем МКР.
 2015-07-14
2015-07-14 716
716