Интегрирование рациональных функций

Краткое содержание лекции

Интегрирование функций, содержащих квадратный трехчлен.

Здесь мы рассмотрим метод нахождения интегралов вида 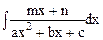и .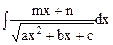

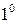. Выносим из квадратного трехчлена 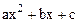коэффициент 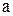и выделяем в нем полный квадрат.

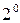Делаем в интеграле замену переменной 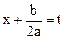, , 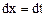в результате он приводится к виду 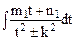или .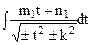

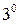Записываем интеграл в виде суммы двух интегралов в соответствии с двумя слагаемыми числителя. В первом интеграле делаем замену переменной 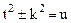. В результате оба слагаемых - табличные интегралы.

Интегрирование рациональных функций

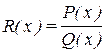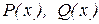Самый важный класс функций, интегралы от которых всегда выражаются через элементарные функции, представляют рациональные функции: , где - многочлены.

Если рациональная дробь неправильная, то с помощью деления 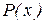на 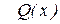можно выделить из нее целую часть и правильную рациональную дробь. Например:

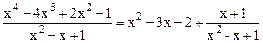
Далее рассматриваем интегрирование только правильных рациональных дробей (т.е. дробей у которых степень многочлена в числителе ниже степени многочлена в знаменателе).

Рассмотрим вопрос о разложении рациональных дробей на простые дроби. Из алгебры известно, что всякий многочлен с вещественными коэффициентами степени выше второй разлагается единственным образом на линейные и квадратичные множители с вещественными коэффициентами.

Пусть многочлен 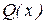разложен на множители в следующем виде:

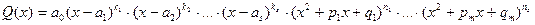
Например. 1) 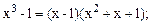2)

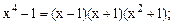
3)

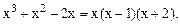
Интегрирование функций вида 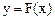, где 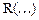- рациональная функция относительно аргументов

С помощью выделения полного квадрата в квадратном трехчлене и замены переменной 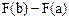интеграл 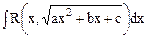приводится к одному из следующих трех видов ( 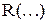-рациональная функция);

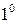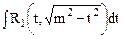. . Здесь с помощью замены переменной 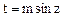, 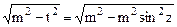= 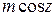, 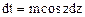этот интеграл преобразуется к виду .

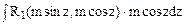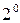. Интегралы вида 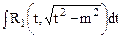находятся с помощью замены 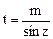, при этом 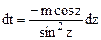, тогда .

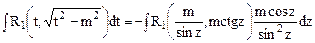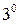. Интегралы вида 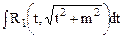находятся с помощью замены 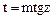, при этом

.

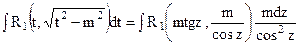Для специальных видов рациональной функции 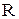иногда проще использовать другие методы нахождения интегралов. Рассмотрим два из них.

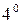. Интегралы вида 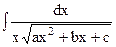находятся с помощью замены переменной , .

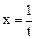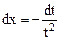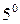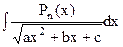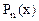. Интеграл , где - многочлен 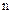-ой степени можно записать в ви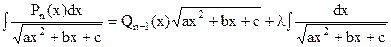де где 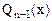- некоторый многочлен степени 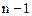, 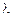-число. Коэффициенты 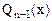и 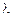находятся методом неопределенных коэффициентов после дифференцирования обеих частей записанного равенства.