Уравнение Шафранова–Грэда

Рассмотрим равновесное стационарное состояние плазмы в системе с замкнутыми магнитными поверхностями. Оно описывается уравнениями двухжидкостной гидродинамики для электронов и ионов соответственно:

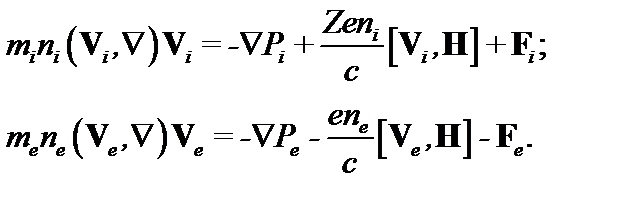(1.1.1)

Здесь F – сила трения между электронами и ионами. Если скорость макроскопического движения плазмы V мала по сравнению с тепловой скоростью V_T, то инерционными членами в левых частях (1.1.1) можно пренебречь. Действительно, градиент давления в правых частях можно представить как nmV_T ²/2 a, где a – характерный масштаб профиля давления. Если масштаб изменения профиля скорости имеет тот же порядок, что и профиль давления, то инерционный член в левых частях (1.1.1) мал по сравнению с градиентом давления. Применимость указанного приблиения нарушается также, если скорость существенно меняется на масштабах, много меньших a. Сложив два уравнения, c учётом j _i = Ze V _i, j _e= ‒ en V _e, j = j _e + j _i, P=P_e+P_i, получаем условие равновесия при дозвуковых скоростях вращения плазмы:

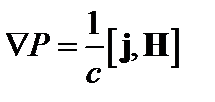. (1.1.2)

Заметим, что мы пренебрегли вязкостью плазмы.

В случае околозвуковых или сверхзвуковых течений член m_i n_i(( 6. ) V _i следует сохранять.

К уравнению (1.1.2) следует добавить стационарные уравнения Максвелла

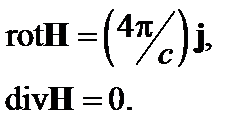(1.1.3)

Умножая скалярно (1.1.2) на H, получаем

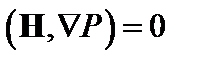. (1.1.4)

Таким образом, давление постоянно вдоль силовых линий.

Умножая то же уравнение на j скалярно, находим, что давление постоянно вдоль линий тока

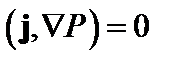. (1.1.5)

В замагниченной плазме можно ввести магнитное давление 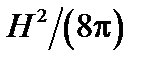. Тогда, используя уравнение (1.1.3) иравенство

,

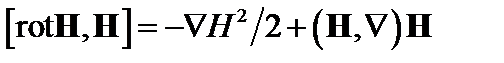условие равновесия (1.1.2) можно переписать через полное давление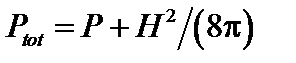

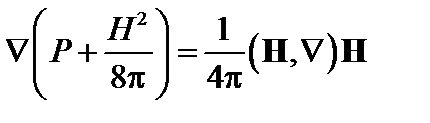. (1.1.6)

В качестве примера рассмотрим простейшую цилиндрически симметричную плазменную конфигурацию, ось которой совпадает с осью z. Пусть ток в такой конфигурации течёт вдоль этой оси. Магнитное поле имеет две составляющие, осевую H_z (r), направленную вдоль оси z, и азимутальную 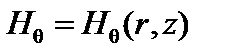. Тогда r и z -компоненты уравнения (1.1.6) имеют вид

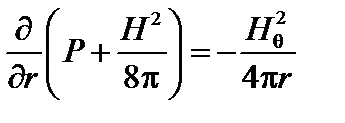; (1.1.7)

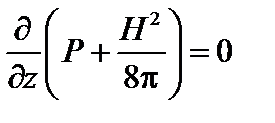. (1.1.8)

Уравнение (1.1.8) означает лишь однородность конфигурации вдоль оси z. Уравнение (1.1.7) должно быть дополнено уравнениями Максвелла. Полученные уравнения выражают давление через магнитное поле, но не могут служить для определения того и другого по отдельности. Эту задачу можно решить только с использованием уравнений переноса.

Для рассмотрения реальных плазменных конфигураций, например, токамака, используется так называемое уравнение Шафранова–Грэда. Оно было получено сначала В.Д. Шафрановым, а затем, независимо от него, Грэдом. Тороидально симметричная конфигурация описывается с помощью системы координат, в которой координатными являются поверхности, параллельные магнитному полю, и перпендикулярные ему. В простейшем случае, описанном выше, такими поверхностями являются поверхност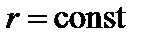и и 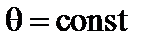соответственно.

Введем цилиндрическую систему координат 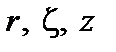, ось симметрии z которой совпадает с осью тора (рис. 1).

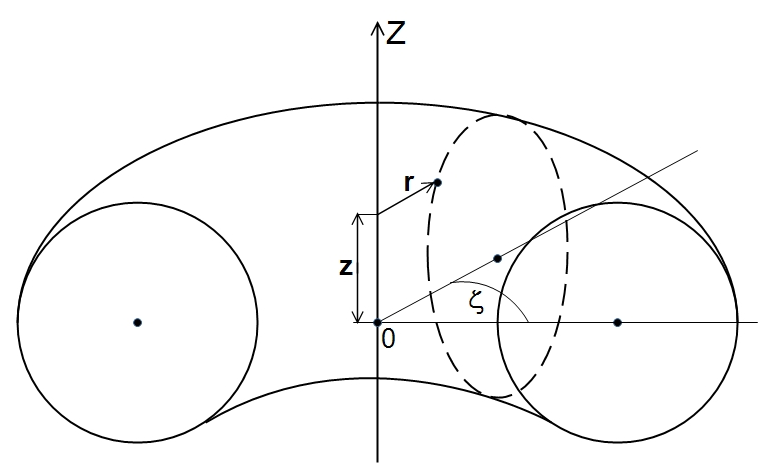
Рис. 1. Тороидальная плазменная конфигурация

Магнитное поле в такой системе может быть описано с помощью двух компонент векторного потенциала 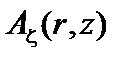и 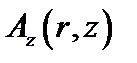. Компоненты магнитного поля выражаются через них следующим образом:

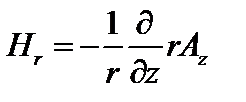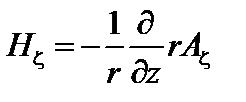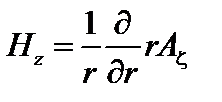_{, , .} (1.1.9)

Здесь мы для удобства правые части разделили и умножили на r.

Введем функцию 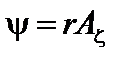. Тогда равенства (1.1.9) перепишутся следующим образом:

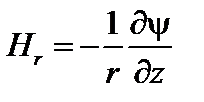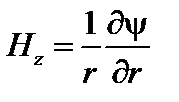; . (1.1.10)

В силу цилиндрической симметрии давление плазмы не зависит от угла 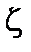. Поэтому условие (1.1.5) можно записать в виде

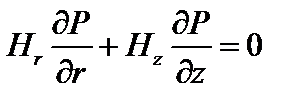. (1.1.11)

Подставляя (1.1.10) в (1.1.11) и учитывая, что 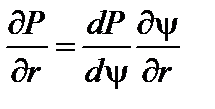и 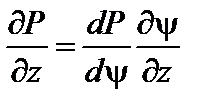, видим, что это условие выполняется, если давление 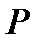зависит только от .

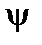Используя (1.1.10), легко видеть, что (H, 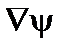) = 0. Это означает, что силовые линии магнитного поля лежат на поверхностях .

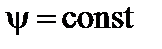В стационарном случае сумма уравнений непрерывности для электронов и ионов дает

div j = 0. (1.1.12)

Таким образом, для тока можно проделать те же операции, что и для H. Аналогично функции 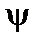можно ввести функцию I, через которую выражаются компоненты тока:

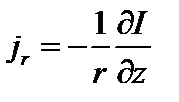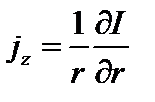; . (1.1.13)

Из условия (j, 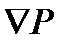) = 0 получаем, что давление плазмы является функцией I.

Тороидальная составляющая магнитного поля легко выражается через функцию I. Действительно, радиальная и осевая составляющие уравнения

rot H = 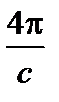j (1.1.14)

принимают вид

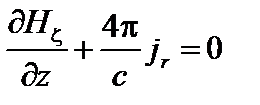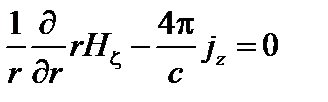; . (1.1.15)

Выражая ток через I, получаем

,

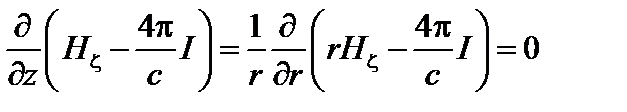то есть

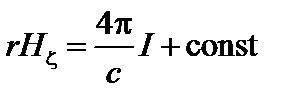, (1.1.16)

причём без ограничения общности константу можно положить равной нулю.

Рассмотрим теперь z -ю составляющую уравнения (1.1.14).

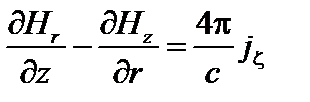. (1.1.17)

Выражая магнитные поля через , это уравнение можно привести к виду

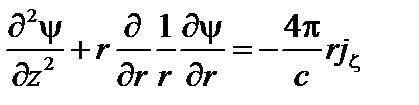. (1.1.18)

Воспользуемся радиальной составляющей уравнения равновесия (1.1.2) и подставим в неё H_z из (1.1.10) и 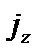из (1.13). Кроме того, учтём, что давление Р зависит только от 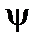. В результате, сократив левую и правую части уравнения на 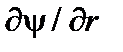, получаем следующее выражение для азимутальной составляющей тока:

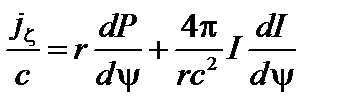. (1.1.19)

Окончательно, подставив теперь это выражение в (1.1.18), получим уравнение Шафранова–Грэда

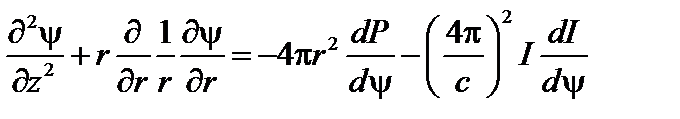. (1.1.20)

Если задать давление и ток как функции магнитных поверхностей, то есть 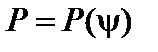, 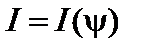(напомним, что ток выражается через производные от функции I), можно найти форму этих поверхностей. Если задать форму магнитных поверхностей 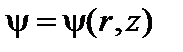, можно найти связь между током и давлением.

В качестве примера рассмотрим тороидально симметричную конфигурацию «сферомак». Его можно представить себе как кольцо с током радиуса R, помещенное во внешнее однородное магнитное поле. Ось симметрии кольца по направлению совпадает с направлением этого поля (рис. 2).

В такой конфигурации полоидальная составляющая тока равна нулю, то есть можно положить 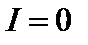. Профиль давления зададим как

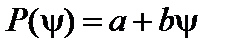. (1.1.21)

Уравнение Шафранова–Грэда в этом случае принимает вид

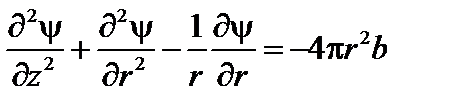. (1.1.22)

Решение этого уравнения можно представить в виде

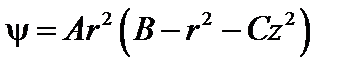, (1.1.23)

если константы A и C связаны соотношением .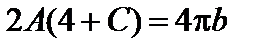

Переопределив константы, выражение (1.1.23) можно переписать в виде

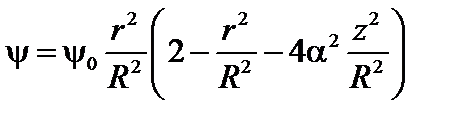. (1.1.24)

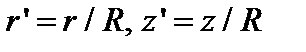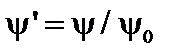Введем безразмерные переменные и . Уравнение магнитных поверхностей 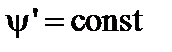в новых переменных принимает вид

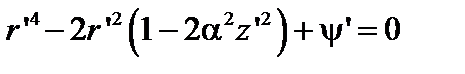(1.1.25)

или

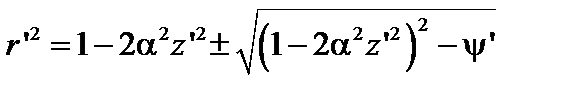. (1.1.26)

Рассмотрим форму магнитных поверхностей при различных значениях :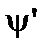

а) 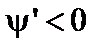. В этом случае для 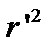имеется одно положительное решение при всех 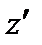. Геометрическим местом точек, соответствующих этому решению, являются цилиндрические поверхности, простирающиеся вдоль оси 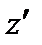от до . В этой области частицы удерживаться не могут.

б) . В этом случае одно из решений представляет собой точку в центре, а другое – эллипсоид, который является сепаратрисой, отделяющей замкнутые магнитные поверхности от разомкнутых.

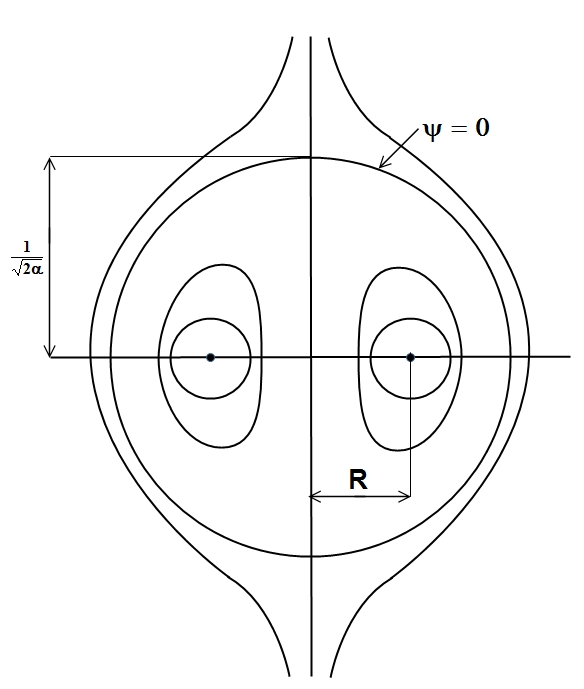
Рис. 2. Сечение магнитных поверхностей сферомака плоскостью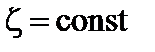

в) 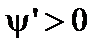. Геометрическими местами точек, соответствующих этому решению, является система вложенных тороидальных поверхностей. Эта область – область удержания плазмы.

Поверхность 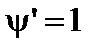вырождается в кольцо, соответствующее магнитной оси системы.

На рис. 2 представлено сечение системы поверхностей плоскостью .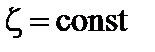

Итак, первым этапом расчёта системы для магнитного удержания плазмы является расчёт равновесия плазмы в магнитном поле. Уравнение Шафранова–Грэда – это статическое нелинейное уравнение. Во-первых, оно может быть обобщено на случай вращающейся плазмы. Во-вторых, оно нелинейное и, следовательно, допускает не единственное решение при одних и тех же граничных условиях.