Геометрическая алгебра

Что же побудило греков избрать геометрический путь развития математики? Почему именно пифагорейцы, научным кредо которых был тезис: «Все есть число», — отвернулись от чисел и перешли к изучению исключительно фигур? Помимо врожденного у греков чувства преклонения перед пластическими формами и зримыми образами, помимо врожденной влюбленности в мягкие линии античной скульптуры и строгую прямолинейность архитектурных памятников тому были и более глубокие причины. Главная из них — это открытие несоизмеримости.

Открытие несоизмеримости разрушало философскую систему пифагорейцев, ибо уже такой простой геометрический объект, как диагональ квадрата со стороной, равной единице, не могла быть измерена известными им числами — целыми числами и их отношениями. Пифагорейцы предприняли интенсивные попытки выхода из этого тупика, и здесь, естественно, просматривалось два пути: либо расширить понятие числа так, чтобы новыми числами стало возможным характеризовать отношение любых двух геометрических отрезков; либо строить математику не на основе арифметики целых чисел и их отношений, а на основе геометрии, определив для геометрических величин все алгебраические операции.

Первый путь на столь ранней ступени развития математики представлял огромные трудности, которые, заметим, были окончательно преодолены лишь в конце XIX в. И пифагорейцы пошли по второму пути — по пути построения алгебры на основе геометрии, по пути геометрической алгебры.

Пифагорейцы отказались от традиционного, ими же разработанного представления чисел в виде дискретных «камешков», укладываемых в правильные фигуры, а стали мыслить числа в виде отрезков, полученных повторением конечного числа раз некоего единичного отрезка. Сложение чисел-отрезков производилось путем приставления одного отрезка к другому вдоль некоторой прямой, вычитание — путем отбрасывания от большего отрезка меньшего. Умножение двух чисел-отрезков представлялось в виде построения прямоугольника на этих отрезках, площадь которого и выражала произведение чисел. Складывать и вычитать, естественно, позволялось только однородные величины (либо только отрезки, либо только площади), поэтому исчисление отрезков было ступенчатым. Наконец, деление определялось как задача «приложения площадей»: «приложить» к данному отрезку c прямоугольник, равновеликий данному прямоугольнику ab, т. е. найти вторую сторону x прямоугольника так, чтобы .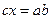

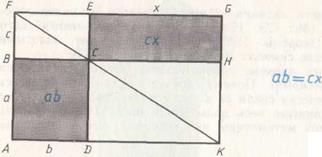
Рис. 63.

«Геометрическое деление» производилось следующим образом. К стороне 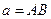прямоугольника ab приставлялся отрезок c, на котором достраивался прямоугольник BCEF (рис. 63). Затем проводилась диагональ FC до пересечения с продолжением стороны AD в точке K и строился внешний прямоугольник AKGF. Тогда затушеванные на рисунке 63 прямоугольники ABCD и CEGH оказывались равновеликими, так как они получались из равных треугольников AFK и FKG путем отбрасывания двух равных часте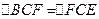й: и 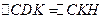. Итак, сторона FG, равная стороне CH прямоугольника CEGH, и есть искомая сторона x.

Геометрически выводились и многие алгебраические соотношения. Например:

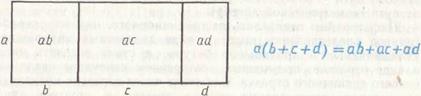
Рис. 64.

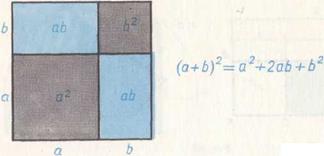
Рис. 65.

Доказательство первых двух тождеств очевидно из рисунков 64 и 65. Для доказательства третьего к прямоугольнику 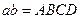достроим квадрат 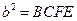, найдем точку G, делящую отрезок AE пополам, т. е. 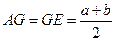, и построим квадрат 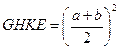(рис. 66). По построению прямоугольник AGMD равен прямоугольнику BEKL, поэтому исходный прямоугольник ABCD равновелик гномону GEKLCM, так как у них GBCM — общая часть, а остальные части равны. Но гномон GEKLCM является разностью двух квадратов: 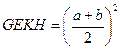и . 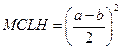Таким образом, 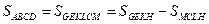, откуда .

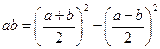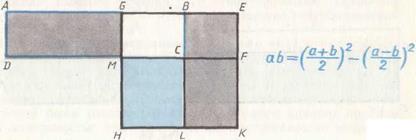
Рис. 66

Однако уже геометрическое представление произведения трех величин требовало пространственных построений, а произведение большего числа сомножителей вообще не поддавалось геометрической интерпретации в пространстве трех измерений. Вот почему античная геометрическая алгебра ограничивалась произведениями двух сомножителей, т. е. основывалась на планиметрии, в которой все построения делались с помощью циркуля и линейки. По этой же причине геометрическая алгебра оказалась хорошо приспособленной для решения квадратных уравнений и фактически этим и ограничивалась.

Пифагорейцами рассматривались три типа геометрических задач, эквивалентных квадратным уравнениям:

1. Построить квадрат, равновеликий прямоугольнику 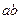. На языке алгебры это означает решить уравнение

2. К данному отрезку a приложить прямоугольник, равновеликий прямолинейной фигуре площади S, так, чтобы «недостаток» был квадратом. Иначе, на отрезке 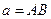построить прямоугольник ACDE площади S так, чтобы прямоугольник CBFD был квадратом (рис. 67). Обозначая сторону квадрата через x, приходим к уравнению

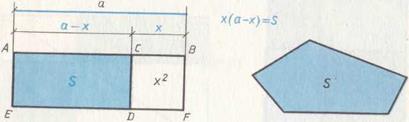
Рис. 67.

3. К данному отрезку a приложить прямоугольник, равновеликий прямолинейной фигуре площади S, так, чтобы «избыток» был квадратом. Иначе, на отрезке построить прямоугольник ACDE площади S так, чтобы прямоугольник BCDF был квадратом (рис. 68). Обозначая сторону квадрата через x, имеем

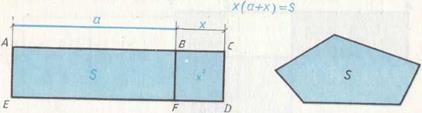
Рис. 68.

Задачи 1 — 3 решались геометрически путем преобразования произведени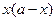й , и 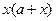в разности квадратов по формуле (2.5.3). Уравнение (2.5.4) при этом принимало вид

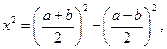
т. е. x, согласно теореме Пифагора, находился как катет прямоугольного треугольника с гипотенузой 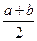и другим катетом 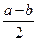. Построением такого треугольника и заканчивается II книга Евклидовых «Начал».

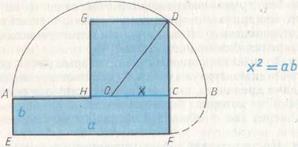
Рис. 69.

Для этого на отрезке 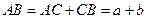как на диаметре строим окружность (рис. 69). Из точки C к прямой AB восстанавливаем перпендикуляр до пересечения с окружностью в точке D. Тогда в треугольнике ODC 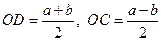и, следовательно, по теореме Пифагора CD и есть искомая величина x. Таким образом, квадрат 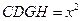будет равновеликим прямоугольнику 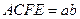. Итак, уравнение 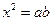решено геометрически, или из величины 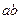геометрически извлечен квадратный корень.

Задачи 2, 3 решаются аналогично, причем задача 2 называлась эллиптической (от ελ-λειψις — недостаток), а задача 3 — гиперболической (от υπερ-βαλλων — избыток). Древнегреческие математики не только нашли общее решение этих задач, но для эллиптической задачи указали ограничение на начальные данные, при котором это решение возможно, а именно

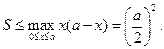
Заметим, что проведенное нами на с. 155 геометрическое построение золотого сечения, т. е. геометрическое построение решения (2.2.2), есть не что иное, как решение гиперболической задачи (2.5.6) при .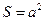

Итак, все задачи, связанные с решением квадратных уравнений, решались пифагорейцами геометрически с помощью циркуля и линейки. Можно доказать и обратное: все задачи на построение циркулем и линейкой эквивалентны решению конечной цепочки квадратных уравнений. Геометрические методы решения этих уравнений были хорошо разработаны, причем никаких проблем с несоизмеримостью при геометрических построениях не возникало. (В самом деле, мы без труда построили золотое сечение или диагональ единичного квадрата, которые, как известно, являются иррациональными величинами.) Казалось, в геометрической алгебре надолго воцарился безоблачный покой.

Однако уже в V в. до н. э. появились задачи, которые никак не удавалось решить с помощью циркуля и линейки. Это знаменитые три классические задачи древности, сыгравшие выдающуюся роль в истории математики и которые были окончательно решены только в XIX в., т. е. через два с половиной тысячелетия! Вот эти задачи:

1. Удвоение куба. Построить куб, объем которого в два раза больше объема данного куба.

2. Трисекция угла. Произвольный угол разделить на три равные части.

3. Квадратура круга. Построить квадрат, равновеликий данному кругу.

Мы остановимся подробно лишь на первой задаче, поскольку ее поразительное по красоте решение было найдено на рубеже V — IV вв. до н. э. последним и наиболее выдающимся представителем пифагорейской школы Архитом. Что касается двух других классических задач, то они также были решены примерно в это же время софистом Гиппием из Элиды и его учеником Диностратом. Гиппий дал способ построения особой линии, называемой квадратрисой [48], с помощью которой и было найдено решение задач о трисекции угла и квадратуре круга. Но ни решение Архита, ни решения Гиппия и Динострата не были классическими решениями классических задач древности, так как они либо привлекали другие построения, кроме построений циркулем и линейкой, либо (как у Архита) выходили из плоскости в пространство.

Начиная с эпохи Возрождения, с возрождением интереса к античному наследию и развитием математики, страсти вокруг классических задач разгораются с новой силой. Простота постановки задач завораживала и притягивала как магнит. Поток «решений» рос как снежный ком, так что в 1775 г. Парижская Академия наук, а вслед за ней и другие академии стали отказываться от рассмотрения этих «решений». Лишь в 1837 г. французский математик Пьер Ванцель (1814 — 1848) доказал, что задачи удвоения куба и трисекции угла сводятся к решению кубических уравнений

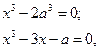
которые неразрешимы в квадратичных радикалах и, значит, не могут быть решены с помощью циркуля и линейки. Еще через 50 лет, в 1882 г., немецкий математик Карл Линдеман (1852 — 1939) доказал трансцендентность (от лат. transcendens — выходящий за пределы) числа π (т. е. тот факт, что число π не удовлетворяет никакому алгебраическому уравнению с целыми коэффициентами), а значит, и невозможность построения квадратуры круга с помощью циркуля и линейки. Так лишь в конце XIX в. была поставлена последняя точка над i в трех классических задачах древности.

Но вернемся к задаче об удвоении куба. Эту задачу называют еще делосской проблемой, ибо с ней связана красивая легенда. Однажды на острове Делос вспыхнула эпидемия чумы. Испуганные жители острова обратились за советом к Дельфийскому оракулу, который сказал, что нужно удвоить золотой жертвенник богу Аполлону, имеющий форму куба. Простодушные делосцы отлили еще один куб и поставили его на первый. Однако чума не унималась. Тогда они вновь обратились к оракулу, и оракул ответил, что они не решили поставленной задачи: новый жертвенник имел вдвое больший объем, но не имел формы куба. Не найдя нужного решения, жители Делоса обратились к Платону, но великий философ ответил уклончиво: «Боги недовольны вами за то, что вы мало занимаетесь геометрией». Платон сам не знал решения задачи, которую вскоре блестяще решил его друг Архит.

Архит из Тарента (ок. 428 — 365 до н. э.) — ярчайшая личность в античной истории. Живое воплощение пифагорейского идеала калокагатии, последний пифагореец, Архит «вызывал к себе удивление народа по причине своего совершенства во всех отношениях» (Диоген Лаэртский). Математик и механик, философ и музыкант, полководец и политический деятель, крупнейший пифагорейский теоретик музыки, Архит первым упорядочил механику на основе математики, работал над деревянной моделью летающего голубя. Как доказал ван дер Варден, Архит является автором арифметической теории пропорций, изложенной в VIII книге «Начал» Евклида. В родном Таренте Архит пользовался исключительным уважением и семь раз избирался стратегом, хотя закон демократического Тарента запрещал одному лицу занимать этот пост дважды. Путем искусных дипломатических маневров Архит вызволил из плена Платона и тем самым спас жизнь великому философу. Таков был «Славный Архит, земель, и морей, и песков исчислитель...» (Гораций).

И все-таки самой яркой страницей в научной биографии Архита является решение делосской проблемы. Если ребро данного куба равно a, а ребро искомого — x, то задача об удвоении куба приводит к уравнению

Сегодня его решение без труда найдет каждый школьник

но вот построит ли он циркулем и линейкой ?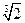

Пифагорейцы не знали иррациональных чисел, поэтому они искали геометрическое решение задачи. В V в. до н. э. Гиппократ Хиосский показал, что решение делосской проблемы можно свести к отысканию двух средних пропорциональных x и y, называемых вставками, которые, будучи «вставленными» между данными величинами a и 2 a, образуют непрерывную пропорцию

В самом деле, из первого равенства имеем 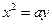, а из второго — 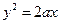. Следовательно,

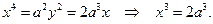
Итак, первая вставка x и есть ребро искомого куба.

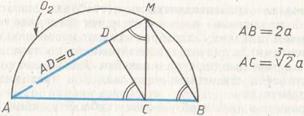
Рис. 70. Треугольник Архита.

Архит заметил, что если из вершины M прямоугольного треугольника, опирающегося на диаметр, опустить перпендикуляр в точку C, а из C опустить перпендикуляр на другой катет (рис. 70), то получится пять подобных треугольников. Назовем их треугольниками Архита. Достаточно рассмотреть три из них:

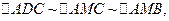
откуда

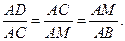
Это и есть непрерывная пропорция вида (2.5.9).

Пусть теперь 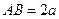и пусть точка M движется по полуокружности диаметра 2 a от точки B к точке A. Тогда точка C будет двигаться по диаметру AB от точки B к точке A, а длина отрезка AD примет все возможные значения от 2 a (при 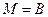) до 0 (при 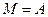). Следовательно, найдется такое промежуточное положение точки M, при котором 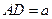. Тогда 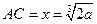и 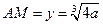. Это и будет решение делосской проблемы. Осталось только найти его.

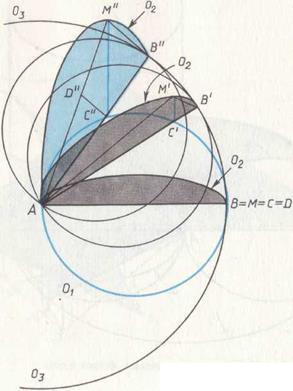
Рис. 71. Пересечение цилиндра и тора.

Для этого Архит фиксирует в плоскости окружность диаметра . Назовем ее . На диаметре AB строится окружность в перпендикулярной плоскости (по этой окружности и будет пробегать точка M). Далее Архит начинает вращать 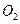вокруг точки A, причем положение точки M на 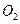определяется положением точки C, которая все время движется по 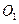. Таким образом, точка M пробегает 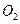от точки B к точке A (рис. 71). Поверхность, которую окружность 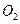опишет в пространстве, будет тором с внутренним диаметром, равным нулю. Поверхность, описываемая в пространстве перпендикуляром CM, будет круговым цилиндром с радиусом a и образующей CM. Наконец, траектория точки M будет линией пересечения 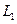тора и цилиндра. Линия 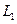в плоскостях, перпендикулярных плоскости окружности 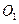, определяет совокупность треугольников Архита (рис. 71), у которых наибольшая гипотенуза постоянна 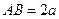, а катет AD изменяется от 2 a (когда ) до 0 (когда ).

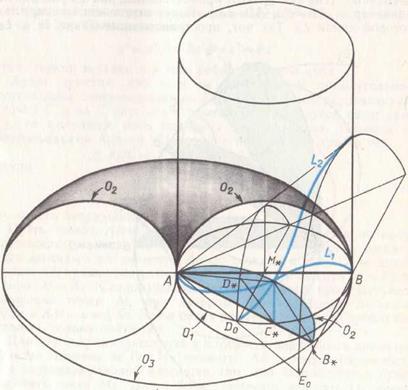
Рис. 72. Пересечение цилиндра, конуса и тора.

Остается «поймать» нужное положение точки M на 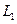, при котором 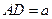. Для этого Архит делает следующее построение (рис. 72). (Для большей наглядности на рисунках 72 — 74 прямая 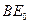показана не как касательная.) Из точки A на окружности 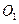откладывается хорда 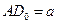, прямая 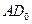продолжается до пересечения в точке 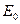с касательной к 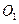в точке B, и затем строится конус с образующей 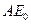и осью AB. Угол полураствора конуса 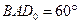(так как 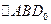прямоугольный, как опирающийся на диаметр, и 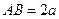, 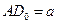). Конус пересекает цилиндр по некоторой линии 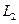. 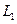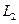Так вот, пространственные линии и пересекаются и их точка пересечения M * и дает искомое положение точки M на окружности 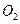или торе. Докажем это.

Рис. 73. Пересечение цилиндра и конуса.

Пусть 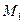— произвольная точка на 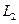(рис. 73). Образующая цилиндра, проходящая через 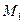, пересекает 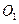в точке 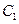. Пусть 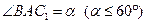, перпендикуляр, опущенный из точки 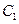на 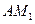, попадает в точку 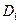, а перпендикуляр, восставленный из точки 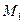к 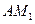, попадает в точку 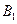и пусть проходящее через 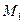круговое сечение конуса пересекает AB в точке 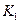. Тогда линия 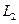также будет определять совокупность треугольников Архита, которые также располагаются в плоскостях, перпендикулярных плоскости окружности 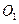. Рассмотрим подробнее эти треугольники.

Из 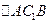находим

Из 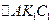, учитывая (2.5.10), имеем

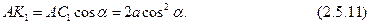
Из 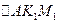, учитывая (2.5.11), находим

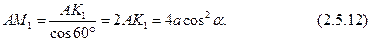
Из 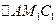, обозначая 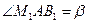и учитывая (2.5.10) и (2.5.12), имеем

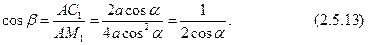
Наконец, из 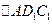, учитывая (2.5.10) и (2.5.13), находим

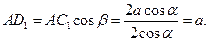
Итак, точк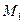и линии 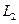определяют треугольники Архита, у которых катет 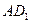постоянен и равен a: 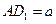, а наибольшая гипотенуза 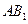изменяется от a (при 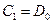) до 8 a (при ).

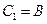Таким образом, линия 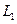определяет треугольники Архита с постоянной гипотенузой 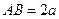, а линия 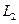в тех же плоскостях определяет треугольники Архита, у которых наибольшая гипотенуза 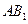изменяется от a до 8 a, а катет 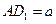постоянен. Из соображений непрерывности следует, что найдется такая точка M * на 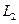, в которой 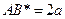. При этом точка 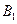треугольников Архита, определяемых линией 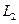(см. рис. 73), попадает на окружность 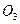, т. е. лежит на поверхности тора (см. рис. 72). 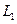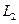Следовательно, линии и пересекаются, и в точке их пересечения у треугольников Архита 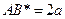, 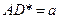и, значит, 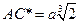, что и дает решение делосской проблемы.

Итак, проекция точки пересечения цилиндра, тора и конуса на окружность 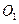— точка C * — определяет решение задачи об удвоении куба.

Не правда ли, полет фантазии Архита поразителен?! «Архита, должно быть, осенило некое поистине божественное вдохновение, когда он нашел это построение»,— писал ван дер Варден. Нам, людям XX в., подчас слишком гордым достижениями века науки и порой высокомерно забывающим, что история цивилизации началась не с нашим пришествием, трудно, но поучительно осознать, что столь блестящие озарения посещали человечество и более двух тысячелетий назад!

И все-таки две тысячи лет развития человечества не прошли даром. Сегодня, когда известны иррациональные числа, аналитическое решение делосской проблемы находится в два действия (см. с. 177), а пользуясь методами аналитической геометрии, можно чисто алгебраически, избегая головоломных построений, найти точку пересечения цилиндра, конуса и тора. Наиболее простое решение задачи получается в цилиндрической системе координат, его любезно предоставил для этой книги студент Московского физико-технического института Роман Малков.

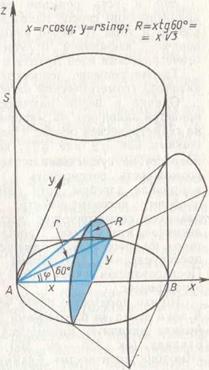
Рис. 74.

Итак, рассмотрим декартову систему координат с началом в центре тора, осью x, совпадающей с осью конуса, осью y, лежащей в плоскости окружности 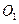и перпендикулярной оси x, и осью z, совпадающей с образующей цилиндра AS. Рассмотрим также цилиндрическую систему координат с тем же центром и той же осью z. Угол φ в цилиндрической системе координат отсчитывается от оси x против часовой стрелки, а полярный радиус r — от начала системы координат в плоскости окружности 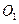Связь декартовой и цилиндрической систем координат очевидна из рисунка 74.

Поскольку тор есть набор окружностей постоянного радиуса a с центром на заданной окружности (в нашем случае — окружности радиуса a), то уравнение тора в цилиндрической системе координат будет иметь вид

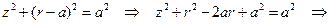
Уравнение цилиндра в декартовой системе координат имеет вид

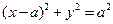
откуда, учитывая связь декартовых координат с цилиндрическими:

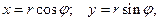
получаем уравнение цилиндра в цилиндрической системе координат:

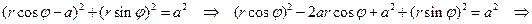
Наконец, конус — это набор окружностей переменного радиуса R с центрами на оси x. Так как угол полураствора конуса равен 60°, то радиус конуса связан с координатой x соотношением 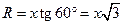. Таким образом, уравнение конуса в декартовой системе координат имеет вид

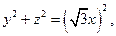
а в цилиндрической системе координат соответственно

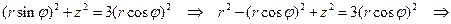
Итак, мы приходим к системе уравнений (2.5.14) — (2.5.16), которая определяет пересечение поверхностей тора, цилиндра и конуса:

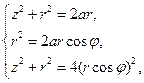
или, вводя новую переменную 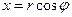, системе вида

Из первого и третьего уравнений системы (2.5.17) имеем

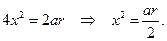
Возводя второе уравнение (2.5.17) в квадрат и подставляя туда найденное выражение для 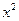, находим

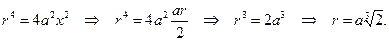
Это и есть решение делосской проблемы. Как видим, аналитический способ нахождения точки пересечения цилиндра, конуса и тора не менее изящен, нежели геометрический, хотя, конечно, изюминкой и этого решения остается блестящая геометрическая идея Архита о пересечении трех поверхностей.

Таково решение делосской проблемы Архита — жемчужины античной геометрической алгебры.

Однако в целом разговор о геометрической алгебре нам придется закончить на минорной ноте. Хотя построение алгебры на геометрической основе и позволило оперировать с величинами (такими, как 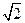или 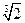), которые в античной теории чисел попросту не существовали, хотя геометрическая форма и дала возможность рассмотреть с общих позиций многие теоремы и правила алгебры, хотя геометрическая алгебра и устранила проблему несоизмеримости, тем не менее при дальнейшем развитии геометрические доспехи, как панцирь, сковали тело античной математики. Прошло время, и «геометрический раствор», на котором была замешена античная алгебра, застыл, и это предопределило дальнейшее увядание античной математики. Последовавшая вскоре гибель всей античной культуры завершила этот процесс.

Но это произошло почти через 1000 лет после пифагорейцев. А пока вслед за блестящими работами последнего пифагорейца Архита античную математику ждали энциклопедический труд Евклида (ок. 356 — ок. 300 до н. э.), гениальное творчество «Ньютона античности» Архимеда (ок. 287 — 212 до н. э.), фундаментальная теория конических сечений Аполлония из Перги (ок. 260 — 170 до н. э.).

Взращенное пифагорейцами древо геометрии еще ждали могучие побеги.

МУЗЫКА