Методические указания
к практическим занятиям по курсу «Молекулярная физика»
Содержание
§1. Таблица необходимых интегралов. 2
§2. Системы координат. 2
Тема 1. Газовые законы.. 7
Тема 2. Уравнение Клапейрона - Менделеева. 7
Тема 3. Вероятность. 8
Тема 4. Статистические распределения. 8
Тема 5. Распределение Максвелла. 9
Тема 6. Применение распределения Максвелла. 10
Тема 7. Распределение Больцмана. 10
Тема 8. Температура. 10
Тема 9. Первое начало термодинамики. 12
Тема 10. Процессы в идеальном газе. 12
Тема 11. Применение первого начала термодинамики. 12
Тема 12. Циклические процессы.. 12
Тема 13. Энтропия. 13
Тема 14. Изменение энтропии в необратимых процессах. 13
Тема 15. Реальные газы.. 13
Тема 16. Эффект Джоуля - Томсона. 14
Тема 17. Фазовые превращения. 14
Тема 18. Критическое состояние вещества. 14
Тема 19. Поверхностное натяжение. 14
Тема 20. Столкновения в газах. 15
Тема 21. Явление переноса в газах. 15
Ответы.. 15
НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ ВОПРОСЫ
Решение задач по физике требует хорошей математической подготовки. В этом разделе даются сведения по математике, которые могут понадобиться при решении задач молекулярной физики.
|
|
|
Таблица необходимых интегралов
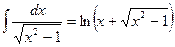
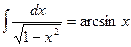
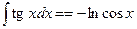
| 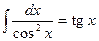
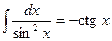
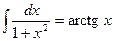
|
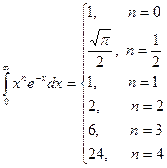
| 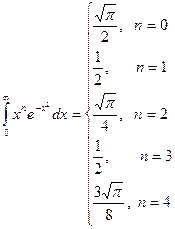
|
Системы координат
Наиболее важными и часто употребляемыми системами координат являются следующие:
1). На плоскости:
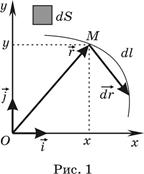 а). Прямоугольная декартова система координат. Начало отсчёта и две взаимно-перпендикулярные оси x и y выбираются произвольно, наиболее рациональным образом для каждой конкретной задачи. Положительные направления осей x и y задаются взаимно-перпендикулярными единичными векторами, соответственно,
а). Прямоугольная декартова система координат. Начало отсчёта и две взаимно-перпендикулярные оси x и y выбираются произвольно, наиболее рациональным образом для каждой конкретной задачи. Положительные направления осей x и y задаются взаимно-перпендикулярными единичными векторами, соответственно, 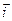 и
и 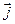 (
(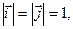
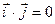 ), образующими векторный базис системы, одинаковый для всех точек плоскости (рис. 1).
), образующими векторный базис системы, одинаковый для всех точек плоскости (рис. 1).
Положение любой точки плоскости, например точки М, задаётся двумя числами, x, и y (x, y Î 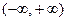 ). Положение точки более компактно можно задать с помощью радиус-вектора
). Положение точки более компактно можно задать с помощью радиус-вектора 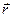 (рис. 1)
(рис. 1)
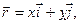 (1)
(1)
Длина радиус-вектора
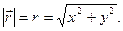 (2)
(2)
Произвольный вектор 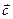 записывается в виде
записывается в виде
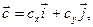 (3)
(3)
где сх и су, соответственно, проекции 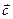 на оси x и y. Длина вектора
на оси x и y. Длина вектора 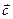
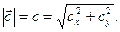 (4)
(4)
Элемент длины дуги кривой (рис. 1)
 (5)
(5)
Площадь элементарной площадки (рис. 1)
dS = dx×dy. (6)
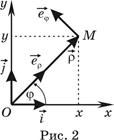
 б). Полярная система координат (рис. 2). Положение произвольной точки плоскости (точки М) задаётся двумя числами r и j
б). Полярная система координат (рис. 2). Положение произвольной точки плоскости (точки М) задаётся двумя числами r и j 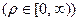 ,
, 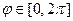 , где r – расстояние от выбранного начала отсчёта до точки М, j – угол, отсчитываемый против часовой стрелки от произвольного направления до направления на эту точку. Ортонормированный базис
, где r – расстояние от выбранного начала отсчёта до точки М, j – угол, отсчитываемый против часовой стрелки от произвольного направления до направления на эту точку. Ортонормированный базис 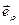 и
и 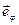 вводится для каждой точки плоскости, т.е. является локальным.
вводится для каждой точки плоскости, т.е. является локальным.
Между декартовыми и полярными координатами точки и базисными векторами существует связь, которую легко найти (рис. 2)
|
|
|
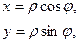
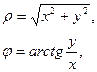 (7)
(7)
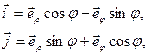
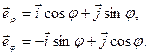 (8)
(8)
Радиус-вектор точки
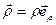 . (9)
. (9)
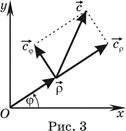
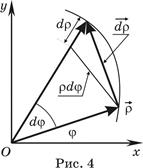 Произвольный вектор
Произвольный вектор 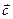 (рис. 3), имеющий начало в точке с координатами r и j записывается в виде
(рис. 3), имеющий начало в точке с координатами r и j записывается в виде
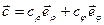 , (10)
, (10)
а его длина
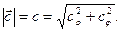 (11)
(11)
Здесь 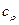 и
и 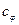 – проекции вектора
– проекции вектора 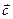 на направления, определяемые векторами
на направления, определяемые векторами 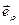 и
и 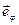 (рис. 3).
(рис. 3).
 Элемент длины дуги некоторой кривой (рис. 4)
Элемент длины дуги некоторой кривой (рис. 4)
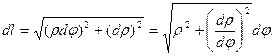 (12)
(12)
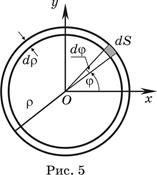
Площадь элементарной площадки (рис. 5)
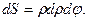 (13)
(13)
В частности, площадь кольца радиуса r и толщины dr легко получить из (13), проинтегрировав по j, (рис. 5)
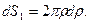 (14)
(14)
2). В пространстве:
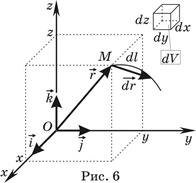 а). Прямоугольная декартова система координат. Положение любой точки в пространстве (например, точки М, рис. 6) определяется тремя числами x, y, z (x, y, z
а). Прямоугольная декартова система координат. Положение любой точки в пространстве (например, точки М, рис. 6) определяется тремя числами x, y, z (x, y, z 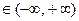 ). Начало отсчёта и направление осей задаётся произвольно тремя взаимно-перпендикулярными единичными векторами
). Начало отсчёта и направление осей задаётся произвольно тремя взаимно-перпендикулярными единичными векторами 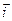 ,
, 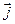 ,
, 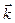 (
(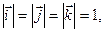
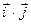 =
= 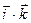 =
= 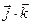 = 0,
= 0, 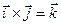 ,
, 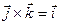 ,
, 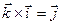 ). Векторы
). Векторы 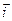 ,
, 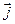 ,
, 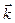 образуют векторный базис, одинаковый для всех точек пространства.
образуют векторный базис, одинаковый для всех точек пространства.
Радиус-вектор точки
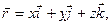 (15)
(15)
его длина
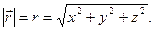 (16)
(16)
Произвольный вектор 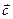 записывается в виде
записывается в виде
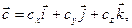 (17)
(17)
где сх, су, сz – проекции 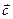 на оси x, y, z. Длина вектора
на оси x, y, z. Длина вектора 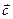
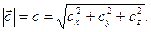 (18)
(18)
Бесконечно малое изменение радиус-вектора при бесконечно малом перемещении точки М вдоль некоторой кривой (рис. 6)
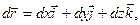 (19)
(19)
Бесконечно малый элемент dl дуги кривой можно считать отрезком прямой, длина которого равна модулю вектора 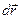 , соединяющего концы этого элемента:
, соединяющего концы этого элемента:
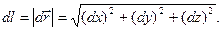 (20)
(20)
Элементарный объём (объём элементарного кубика, рис. 6)
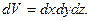 (21)
(21)
Площади элементарных площадок, перпендикулярных осям координат, равны площадям dy×dz, dz×dx, dx×dy соответствующих боковых граней элементарного кубика (рис. 6)
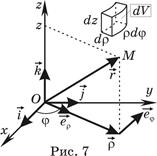
б). Цилиндрическая система координат. Положение точки M пространства (рис. 7) определяется тремя числами r, j, z (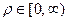 ,
, 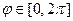 ,
, 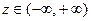 ).
).
 Для каждой точки пространства вводится локальный базис
Для каждой точки пространства вводится локальный базис 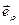 ,
, 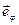 ,
, 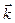 (рис. 6), (
(рис. 6), (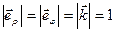 ,
, 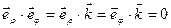 ,
, 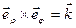 ,
, 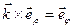 ,
, 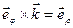 ).
).
Радиус-вектор точки
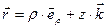 , (22)
, (22)
его длина
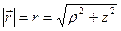 . (23)
. (23)
Между декартовыми и цилиндрическими координатами точки и базисными векторами существует связь
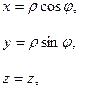
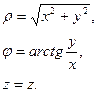 (24)
(24)
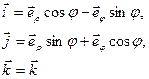
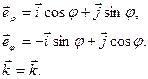 (25)
(25)
Длина элемента дуги кривой
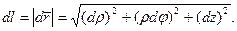 (26)
(26)
Площадь элементарной площадки цилиндрической поверхности, радиус которой r
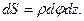 (27)
(27)
Элементарный цилиндрический объём на расстоянии r от оси z (рис. 7)
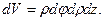 (28)
(28)
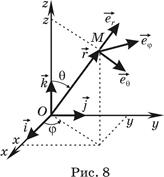 в). Сферическая система координат. Положение точки M пространства определяется тремя числами r, q, j (
в). Сферическая система координат. Положение точки M пространства определяется тремя числами r, q, j (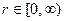 ,
, 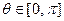 ,
, 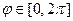 ). Ортонормированный базис
). Ортонормированный базис 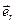 ,
, 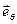 ,
, 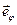 также является локальным и вводится, как показано на рисунке 8: (
также является локальным и вводится, как показано на рисунке 8: (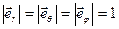 ,
, 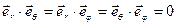 ,
, 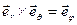 ,
, 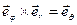 ,
, 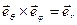 ).
).
Радиус-вектор точки
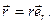 (29)
(29)
Из рисунка 8 нетрудно найти связь между декартовыми и сферическими координатами точки, а также связь между базисными векторами
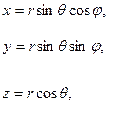
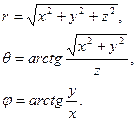 (30)
(30)
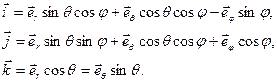 (31)
(31)
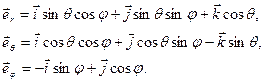 (32)
(32)
Длина элемента дуги кривой
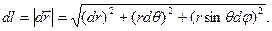 (33)
(33)
Площадь элементарной сферической поверхности радиуса r
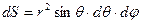 . (34)
. (34)
Объём элементарного кубика
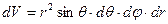 . (35)
. (35)
В частности, объём сферического слоя радиуса r и толщины dr легко находится из (34) путём интегрирования по углам q и j:
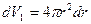 . (36)
. (36)
Кроме углов на плоскости, в математике и физике используются объёмные или телесные углы, которые характеризует угол зрения, под которым из точки (вершины угла) видно тело или некоторая поверхность.
Телесный угол – это часть пространства, ограниченная поверхностью, образованной прямыми линиями, проведенными из одной точки (вершины) ко всем точкам видимой границы тела или поверхности. Телесный угол, под которым из центра сферы радиусом r видна площадь DS её поверхности,
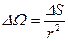 . (37)
. (37)
В сферической системе координат бесконечно малый телесный угол
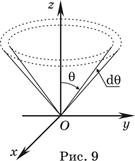
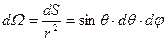 . (38)
. (38)
Интегрируя по углу j в пределах от 0 до 2p, получим выражение для бесконечно малого телесного угла, заключённого между двумя коническими поверхностями с общей вершиной и осью z, углы раствора которых равны q и q + dq (рис. 9).
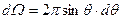 . (39)
. (39)
Интегрируя последнее соотношение по q в пределах от 0 до q, получим выражение для конечного телесного угла
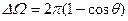 . (40)
. (40)
При q = p получаем полный телесный угол
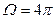 . (41)
. (41)
Для описания движения молекул в некоторых случаях удобно использовать математическое пространство скоростей, в котором координаты x, y. z заменяются проекциями скоростей ux, uy, uz, а радиус-вектор 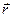 – вектором скорости
– вектором скорости 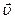 .
.
|
|
|
 2015-09-06
2015-09-06 1155
1155







