Что, несомненно, должен знать и уметь делать каждый грамотный пользователь теста — это понимать, что такое тестовые нормы и как ими пользоваться.
Первоначальный суммарный балл, подсчитанный с помощью ключа, не является показателем, который можно диагностически интерпретировать. Его называют в тестологии «сырым тестовым баллом». Применение тестовых норм в профессионально организованной психодиагностике основывается на переводе тестовых баллов из «сырой» шкалы в «стандартную». Эта процедура называется «стандартизация тестового балла».
■
Психодиагностика как научная технология
Пусть мы провели тест из 20 заданий и испытуемый дал 12 правильных ответов. Можно ли при этом сказать, что способность у испытуемого выражена лучше или хуже, чем в среднем? Нет. Для такого вывода нужно сравнить балл 12 со средним баллом по представительной выборке испытуемых.
Выборка, на которой определяются статистические тестовые нормы, называется ВЫБОРКОЙ СТАНДАРТИЗАЦИИ. Ее численность, как правило, не меньше 200 человек. Столько должны принять участие в психометрическом эксперименте по определению тестовых норм — в эксперименте по стандартизации теста.
Если после стандартизации теста выясняется, к примеру, что среднее арифметическое по сырой шкале теста равно 14, то оказывается балл 12 — это не лучше, а хуже среднего (хотя испытуемый и справился больше, чем с половиной заданий). Просто в данном случае тест содержит слишком простые задания, несколько отклоняется по этому параметру от оптимальной трудности.
Простейшая ЛИНЕЙНАЯ СТАНДАРТИЗАЦИЯ тестового балла производится по формуле
■ 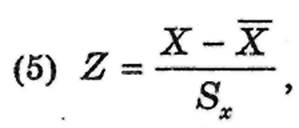
где Z — стандартный балл на так называемой стандартной шкале Z (с центром 0 и отклонением 1), X — сырой балл по тесту,. 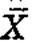 — средний балл по выборке стандартизации, S — стандартное отклонение по выборке стандартизации.
— средний балл по выборке стандартизации, S — стандартное отклонение по выборке стандартизации.
После получения стандартного балла Z можно перевести тестовый балл в любую стандартную тестовую шкалу, принятую в психодиагностике. Например, перевод в шкалу IQ производится по формуле
Основы психодиагностики
IQ= Z..15 + 100.
Напомним, что в шкале IQ центр равен 100, а отклонение равно 15.
Если перевод требуется в так называемую шкалу «стенов» (от английского «standard ten» — стандартная десятка), то формула пересчета из шкалы Z выглядит так:
Sten = Z...2+ 5.5,
так как в шкале стенов центр равен 5.5, а отклонение равно 2.
Обобщенная формула перевода сырого балла в заданную стандартную шкалу имеет вид:
(6) Y =Ss • Z + М,
где Y — стандартный балл по произвольной шкале с центром М и отклонением S$.
Для серьезных профессиональных тестов вместо описйнной здесь простейшей линейной'стандартизации используется более сложная процедура нелинейной нормализации (форсированный переход к нормальному распределению). В результате этой, более точной, процедуры разработчики снабжают пользователей теста так называемой «КОНВЕРСИОННОЙ ТАБЛИЦЕЙ» для перевода сырых баллов в стандартные баллы по заданной шкале. В ней приводится полный перечень соответствий между интервалами сырой шкалы и интервалами стандартной.
Ниже приведен пример того, как может выглядеть конверсионная таблица для некоторого теста арифметических вычислений из 30 заданий. Простейшая процедура подсчета баллов (за правильный ответ — 1 очко, за ошибку — 0) дает нам сырую шкалу от 0 до 30:
Психодиагностика как научная технология
Таблица 1
Пример фрагмента конверсионной таблицы для перевода сырых баллов в стены
| Сырой балл | 0-6 | 7-8 | 8-9 | 10-13 | 14-16 | 17-19 | 20-22 | 23-24 | 26-30 | |
| Стены |
Как пользоваться таблицей? Если испытуемый показал 5 сырых очков (решил только 5 заданий), то ему ставится минимальный стандартный балл 1. Если испытуемый решил 25 заданий, то — балл 9.
После того, как балл по тесту стандартизирован, можно выносить диагностическое заключение. Общее правило здесь таково: если стандартный балл У превышает единицу «верхней» (или «высокой») группы M+Ss, то данному испытуемому приписывается повышенное значение измеренного психического свойства. Например, про ученика говорят, что он является определенно более дисциплинированным, чем средний ученик в российской школе (или московской, или иркутской — в зависимости от того, на какой выборке стандартизации получены нормы). Если же стандартный балл Y ниже границы «нижней» («низкой») группы M-Ss, то о данном испытуемом формулируется заключение, соответствующее низкому полюсу измеряемого свойства. Если стандартный тестовый балл Y заключен в пределах центрального интервала (M-Ss, M+Ss), то про испытуемого говорят, что у него измеренное свойство выражено в средней степени — как у большинства
людей.
На шкале стенов граница «верхней» группы равна 7.5, а «нижней» — 3.5, то есть при получении 8 стенов и больше испытуемый зачисляется в «верхнюю» группу; а при получении 3 стенов и меньше —
■
в «нижнюю».
Если мы имеем дело с биполярным (двухполюсным) психическим свойством, например, «гибкость — ригидность», то для «высокой» группы формулируется заключение как для «гибких» людей, а для «низкой» группы — как для ригидных людей. Соответственно средняя группа из центрального интервала признается нейтральной, неполяризованнои по данному тестовому параметру.
Любые тестовые заключения при использовании статистических тестовых норм являются относительными. Они зависят от той выборки, на которой производилась стандартизация теста. То, насколько выборка стандартизации позволяет применять тест на широкой популяции, называется РЕПРЕЗЕНТАТИВНОСТЬЮ тестовых норм. [Примечание. Под популяцией обычно понимают категорию испытуемых определенной социальной, профессиональной или половозрастной принадлежности]. Репрезентативность— третье важнейшее психометрическое свойство теста. Понимание смысла этого требования к тесту помогает правильно учитывать ограничения в сфере применения теста.
Например, если тест проходил стандартизацию на студентах, то перед его применением на школьниках следует вначале произвести РЕСТАНДАРТИ-ЗАЦИЮ, то есть снова собрать тестовые нормы на представительной выборке, сформированной именно из школьников. В противном случае диагностические выводы будут производиться по неадекватным тестовым нормам и будут неточны и неверны.
Проверка репрезентативности тестовых норм осуществляется с помощью анализа так называемого распределения частот тестовых баллов. Одним из простейших методов является проверка нормальности этого распределения. Более сложный и универсальный подход предполагает сравнение двух рас-
Психодиагностика как научная технология
пределений, построенных для двух случайных половин выборки стандартизации. Если два этих распределения оказываются практически тождественными, то можно говорить о репрезентативности тестовых норм (более подробно об этом см. уже указанные специализированные издания по психометрике).
Введение понятия репрезентативности позволяет нам дать более строгое определение того, что такое стандартизация теста. О СТАНДАРТИЗАЦИИ ТЕСТА в строгом смысле можно говорить, когда задана полная таблица соответствия сырой шкалы и стандартной шкалы и содержание этой таблицы обосновано статистической структурой распределения тестовых баллов на выборке стандартизации.
Кроме статистических тестовых норм в современных тестах часто используются КРЙТЕРИАЛЬНЬШ НОРМЫ. Они особенно важны для сферы образования. Действительно, что дает нам знание о том, что Петров выполнил тест лучше среднего испытуемого, если средний испытуемый тоже не справился с боль-: шинством заданий и мы прогнозируем, что подавляющее большинство испытуемых без специального дополнительного обучения не смогут показать требуемого уровня эффективности в будущей деятельности.
При построении так называемого «теста по критерию» шкала сырых тестовых баллов калибруется особыми реперными точками, которые соответствуют уровням рассчитанной вероятности достижения какого-то критерия (заданной эффективности деятельности). Например, если оператор АЭС был точен в 45 из 48 процентов заданий, то это может еще и не соответствовать требуемому уровню критериальной «надежности оператора» (в данном случае «надежность» — измеряемое свойство), а вот если он был точен в 47 из 48 заданий, то это может считаться достаточным уровнем «надежности». Таким образом,
Основы психодиагностики
при построении диагностических заключений по критериальным тестам мы интересуемся не степенью отклонения балла от центра шкалы, а достижением или недостижением какого-то критического уровня на шкале.
 2015-10-13
2015-10-13 822
822








