Каждой квадратной матрице 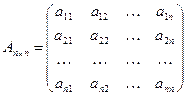 можно поставить в соответствие выражение, которое называется определителем (детерминантом) матрицы
можно поставить в соответствие выражение, которое называется определителем (детерминантом) матрицы 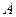 , и обозначается символом:
, и обозначается символом: 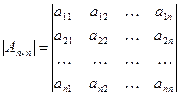 или
или 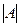 (det
(det 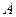 ).
).
Определителем квадратной матрицы второго порядка 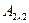 называется число, обозначаемое символом
называется число, обозначаемое символом 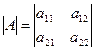 и определяемое равенством
и определяемое равенством
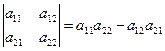 . (2.1)
. (2.1)
Определитель третьего порядка вычисляется по формуле
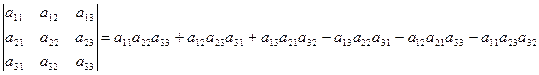 . (2.2)
. (2.2)
Для вычисления определителей третьего порядка по формуле (2.2) применяют символическую схему Саррюса (правило «треугольников»):
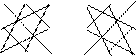
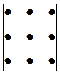 =
= 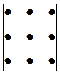 —
— 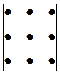 .
.
Минором 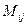 элемента
элемента 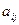 определителя
определителя 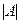 порядка
порядка 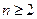 называется определитель порядка
называется определитель порядка 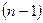 , полученный из
, полученный из 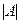 вычеркиванием
вычеркиванием 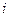 -ой строки и
-ой строки и
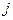 -ого столбца, в пересечении которых стоит элемент
-ого столбца, в пересечении которых стоит элемент 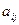 .
.
Алгебраическим дополнением 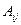 элемента
элемента 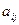 называется его минор, взятый со знаком «+», если сумма
называется его минор, взятый со знаком «+», если сумма 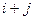 - четное число, и со знаком «-», если эта сумма нечетная:
- четное число, и со знаком «-», если эта сумма нечетная:
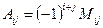 . (2.3)
. (2.3)
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
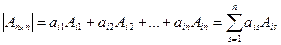 (2.4)
(2.4)
(разложение по элементам 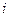 -ой строки,
-ой строки, 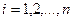 ).
).
|
|
|
Аналогично, разложение определителя по элементам 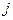 -го столбца имеет вид:
-го столбца имеет вид:
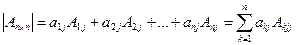 . (2.5)
. (2.5)
Простейшие свойства определителей:
1. При транспонировании определителя его значение не изменяется.
2. При перестановке двух любых строк (или столбцов) определитель меняет свой знак.
3. Если две строки (или два столбца) определителя одинаковы, то он равен нулю.
4. Общий множитель всех элементов строки (или столбца) определителя можно вынести за знак определителя.
5. Если все элементы какой-нибудь строки (или столбца) определителя равны нулю, то определитель равен нулю.
6. Значение определителя не изменится, если к элементам одной строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на число 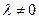 .
.
Задача 2.1. Вычислить определитель 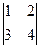 .
.
Решение. 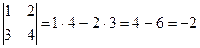 .
.
Задача 2.2. Вычислить определитель 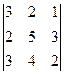 .
.
Решение. Покажем, что результат вычисления определителя не зависит от выбора метода решения задачи. Применим схему Саррюса. По формуле (2.2) имеем
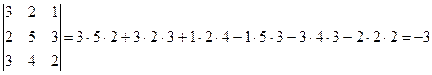 .
.
Используя теорему Лапласа, по формуле (2.4) получаем
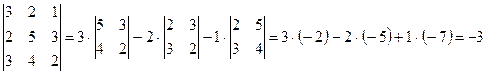 .
.
Задача 2.3. Решить уравнение 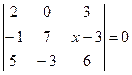 .
.
Решение. Разложим определитель по второй строке:
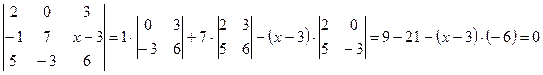 .
.
Решая теперь уравнение 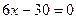 , получим
, получим 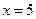 .
.
Задача 2.4. Вычислить определитель приведением к «треугольному виду»:
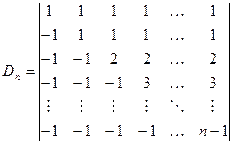 .
.
Решение. Прибавляя к каждой строке определителя соответствующие элементы первой строки, получим:
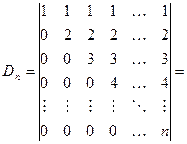
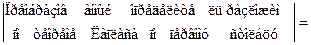
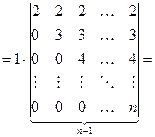
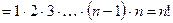
 2015-10-14
2015-10-14 7415
7415








