Приклади розв’язування типових задач

Задача 2.1. У грошо-речовій лотереї на кожну 1000 квитків випадає 25 грошових і 15 речових виграшів. Куплено два квитка. Яка ймовірність, що випаде: 1) на перший квиток грошовий виграш, а на другий – речовий виграш; 2) хоча б на один квиток виграш?

Розв’язання. 1) Позначимо через Р(А) ймовірність грошового виграшу на перший квиток, Р(В/А) – ймовірність речового виграшу на другий квиток. Тоді ймовірність виграти гроші на перший квиток і якусь річ на другий буде Р(АВ)=Р(А) Р(В/А).

За класичним означенням ймовірності

Р(А) = 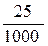, Р(В/А) = 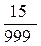. Тоді Р(АВ) =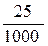 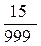»0,000375.

2) Позначимо через С виграш на перший квиток, а через D – на другий квиток. Тоді ймовірність хоча б на одного виграшу на два квитка буде Р(С+D)=Р(С)+Р(D)-Р(СD).

За класичним означенням ймовірності Р(С)=Р(D)= 40/1000, тоді Р(D/С) =39/999. За теоремою добутку ймовірностей Р(СD)=Р(С)Р(D/С) =40/1000 39/999»0,00156. Отже, Р(С+D) =40/1000+40/1000–0,00156»0,07844.

Відповідь: 1)»0,000375; 2) 0,07844.

Задача 2.2. Три стрільці незалежно один від одного стріляють по цілі. Ймовірність влучення в ціль для першого стрільця дорівнює 0,75, для другого – 0,8, для третього – 0,9. Визначити ймовірність того, що а) всі три стрільці одночасно влучать в ціль; б) в ціль влучить хоча б один стрілок.

Розв’язання. а) Позначимо через Р(А) ймовірність влучення в ціль для першого стрільця, через Р(В) – для другого стрільця, через Р(С) – для третього стрільця. За умовою Р(А) =0,75, Р(В) =0,8, Р(С) =0,9.

За теоремою добутку ймовірностей три стрільця одночасно влучать в ціль з ймовірністю

Р(АВС)= Р(А) ∙ Р(В) ∙ Р(С)= 0,75∙0,8∙0,9=0,54.

б)Ймовірність промаху першого стрільця Р(Ā) =1–0,75=0,25, для другого стрільця – Р(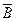) =1–0,8=0,2, для третього – Р(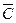) =1–0,9=0,1, тоді ймовірність промаху всіх стрільців одночасно

Р(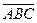) = Р(Ā) ∙ Р(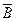) ∙ Р(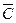) =0,25∙0,2∙0,1=0,005.

Подія, що заключається у влучанні в ціль хоча б одного стрільця, протилежна події Р(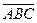), тому Р =1– Р(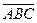) =1–0,005=0,995.

Відповідь: а) 0,54; б)0,995.

Розділ ІІІ. Випадкова величина. Закон розподілу випадкової величини. Числові характеристики випадкової величини. Визначення характеристик випадкових величин на основі дослідних даних

Під випадковою величиною розуміють числову величину, яка з’являється у результаті стохастичного експерименту.

Дискретною називають випадкову величину, можливими значеннями якої є окремі ізольовані числа, які ця величина приймає з певними ймовірностями. Іншими словами, можливі значення дискретної випадкової величини можна перенумерувати. Число можливих значень дискретної випадкової величини може бути скінченим або нескінченим (але зчисленим).

Якщо значення, які може приймати дана випадкова величина Х, заповнюють скінчений чи нескінчений проміжок (а, b) числової осі Ох, то випадкова величина називається неперервною.

Співвідношення, яке дає можливість встановити тим чи іншим способом зв’язок між можливими значеннями випадкової величини і їх відповідними ймовірностями, називають законом розподілу випадкової величини.

Закон розподілу дискретної випадкової величини Х може бути заданий рядом розподілу: у вигляді таблиці, перша строчка якої містить можливі значення х_і, а друга – ймовірності р_і:

Таблиця 5.1.

Х	х₁	х₂	...	х_п
Р	р₁	р₂	...	р_п

причому р₁+р₂+...+р_п =1.

Якщо множина можливих значень Х нескінчена (злічена), то ряд р₁+р₂+...+р_п+... збігається і його сума дорівнює одиниці.

Інколи закон розподілу дискретної випадкової величини Х задають аналітично (у вигляді формули) Р (Х = х_і) = φ (х_і) або за допомогою функції розподілу.

Закон розподілу дискретної випадкової величини Х можна зобразити графічно, для чого в прямокутній системі координат будують точки М ₁ (х ₁; р ₁), М ₂ (х ₂; р ₂),..., М_п (х_п; р_п), де х_і – можливі значення Х, р_і – відповідні ймовірності, і з’єднують їх відрізками прямих. Отриману фігуру називають многокутником розподілу.

Закон розподілу неперервної випадкової величини Х зручно задавати за допомогою функції щільності ймовірності р (х). Ймовірність Р (a<Х<b) того, що значення, яке приймає випадкова величина Х, попадає в проміжок (а, b), визначається рівністю:

Р (a<Х<b) = 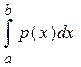. (5.1)

Графік функції р (х) називається кривою розподілу. Геометрично ймовірність попадання випадкової величини в проміжок (а, b) дорівнює площі відповідної криволінійної трапеції, обмеженої кривою розподілу, віссю Ох і прямими х=а, х=b.

Функція F (x)= P (X < x) називається функцією розподілу ймовірності випадкової величини Х. Функція F (x) існує як для дискретних, так і для неперервних випадкових величин. Якщо р (х) – функція щільності розподілу ймовірності неперервної випадкової величини Х, то

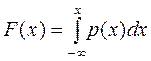. (5.2)

З рівності (5.2) випливає, що р (x)= F ' (x).

Інколи функцію р (x) називають диференціальною функцією розподілу ймовірності, а функцію F (x) – інтегральною функцією розподілу ймовірності.

Поняття функції розподілу є центральним в теорії ймовірностей. Використовуючи це поняття, можна дати інше означення неперервної випадкової величини. Випадкова величина називається неперервною, якщо її інтегральна функція розподілу F (x) неперервна.

Математичним сподіванням дискретної випадкової величини називається сума добутків значень випадкової величини на ймовірності цих значень.

Якщо випадкова величина Х характеризується рядом розподілу (таблиця 5.1), то математичне сподівання М (Х) визначається за формулою:

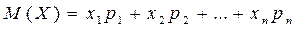або 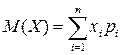. (5.3)

Якщо n =∞, то 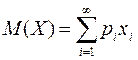(за умови, що ряд абсолютно збігається).

Поняття математичного сподівання розповсюджується й на неперервну випадкову величину. Нехай р (х) – щільність ймовірності випадкової величини Х. Тоді математичне сподівання неперервної випадкової величини Х визначається рівністю

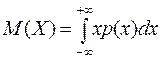(5.4)

(за умови, що інтеграл абсолютно збігається).

Геометрично математичне сподівання як неперервної, так і дискретної випадкової величини дорівнює абсцисі центра ваги площі, обмеженої кривою (або полігоном) розподілу і віссю абсцис. Тому при симетрії кривої (або полігону) розподілу відносно деякої прямої, паралельної до осі ординат, М (Х) співпадає з абсцисою точки перетину цієї осі симетрії з віссю абсцис.

Точка осі Ох, що має абсцису, рівну М (Х), називається центром розподілу цієї випадкової величини.

Дисперсією випадкової величини Х називають математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання:

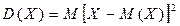. (5.5)

Якщо ввести позначення M (X)= m, то формули для обчислення дисперсії дискретної випадкової величини Х запишуться у вигляді:

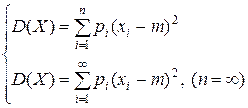, (5.6)

а для неперервної випадкової величини Х – у вигляді:

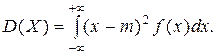(5.7)

Для дисперсії випадкової величини справедлива формула:

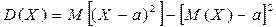. (5.8)

де а – довільне число. Такою формулою часто користуються для обчислення дисперсії випадкової величини, так як обчислення за цією формулою як правило простіші, ніж за формулами (5.6) і (5.7).

Середнім квадратичним відхиленням випадкової величини Х називається величина:

. (5.9)