Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой системе координат оси абсцисс, называется действительной осью, а оси ординат - мнимой осью (рис. 1).

Комплексному числу  будет однозначно соответствовать на комплексной плоскости точка
будет однозначно соответствовать на комплексной плоскости точка 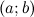 :
:  (рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.
(рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.
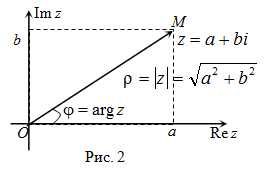
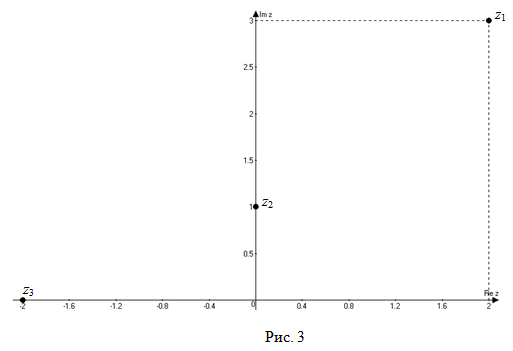
Например. На рисунке 3 на комплексной плоскости изображены числа  ,
, 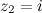 и
и  .
.
Модуль комплексного числа
Комплексное число также можно изображать радиус-вектором  (рис. 2). Длина радиус-вектора, изображающего комплексное число
(рис. 2). Длина радиус-вектора, изображающего комплексное число  , называется модулем этого комплексного числа.
, называется модулем этого комплексного числа.
Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.
Модуль вычисляется по формуле:
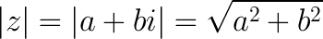
То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.
Задание. Найти модуль комплексного числа 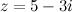
Решение. Так как 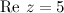 ,
, 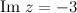 , то искомое значение
, то искомое значение
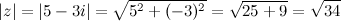
Ответ. 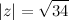
Иногда еще модуль комплексного числа обозначается как  или
или 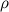 .
.
Аргумент комплексного числа
Угол  между положительным направлением действительной оси и радиус-вектора
между положительным направлением действительной оси и радиус-вектора  , соответствующим комплексному числу
, соответствующим комплексному числу  , называется аргументом этого числа и обозначается
, называется аргументом этого числа и обозначается 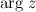 .
.
Аргумент  комплексного числа
комплексного числа  связан с его действительной и мнимой частями соотношениями:
связан с его действительной и мнимой частями соотношениями:
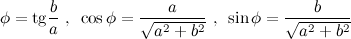
На практике для вычисления аргумента комплексного числа обычно пользуются формулой:
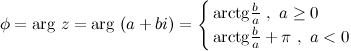
Задание. Найти аргумент комплексного числа 
Решение. Так как 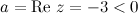 , то в выше приведенной формуле будем рассматривать вторую строку, то есть
, то в выше приведенной формуле будем рассматривать вторую строку, то есть
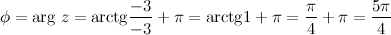
Ответ. 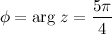
Аргумент действительного положительного числа равен 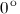 , действительного отрицательного -
, действительного отрицательного - 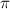 или
или 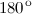 . Чисто мнимые числа с положительной мнимой частью имеют аргумент равный
. Чисто мнимые числа с положительной мнимой частью имеют аргумент равный 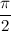 , с отрицательной мнимой частью -
, с отрицательной мнимой частью - 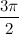 .
.
У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).
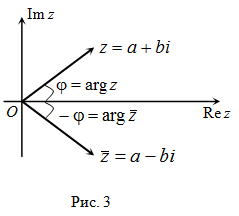
Тригонометрическая форма комплексного числа
Пусть задано комплексное число  . Как известно, его можно изобразить на комплексной плоскости точкой, абсцисса которой равна действительной части этого числа, то есть
. Как известно, его можно изобразить на комплексной плоскости точкой, абсцисса которой равна действительной части этого числа, то есть  , а ордината - мнимой части
, а ордината - мнимой части  (рис. 1).
(рис. 1).

Абсциссу  и ординату
и ординату  комплексного числа
комплексного числа  можно выразить через модуль
можно выразить через модуль  и аргумент
и аргумент  следующим образом:
следующим образом:
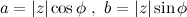
В данном случае  и
и 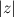 удовлетворяют соотношениям:
удовлетворяют соотношениям:

Тогда
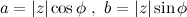
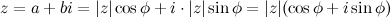
Таким образом, для всякого комплексного числа  справедливо равенство
справедливо равенство

которое называется тригонометрической формой комплексного числа  .
.
Задание. Комплексное число  представить в тригонометрической форме.
представить в тригонометрической форме.
Решение. Для заданного числа действительная часть 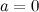 , а мнимая часть
, а мнимая часть 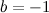 . Тогда модуль этого числа
. Тогда модуль этого числа

а аргумент
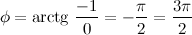
Отсюда получаем, что
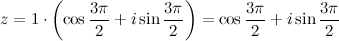
Ответ. 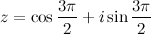
 2015-10-22
2015-10-22 1978
1978








